图文解说：微积分的本质——隐函数求导（Implicit differentiation）

Posted 2021-09-28 鸿渐之翼

“Do not ask whether a statement is true until you know what it means.”
——Errett Bishop
“明白一句话的意义之前，不要去问它是否正确。”
——埃雷普.毕肖普（美国实分析数学家）
当我们初学微积分时，总是有疑问。
这个圆可以表示方程x2+y2 =5*2

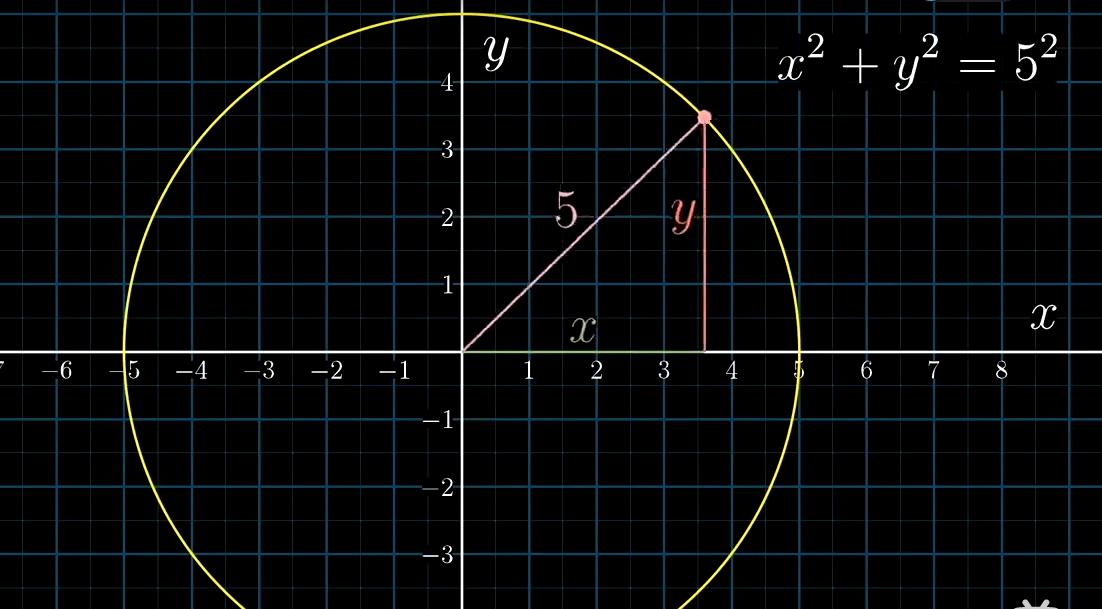
即圆心到圆上的距离都是5，按照勾股定理，三角形直角边边长的平方和等于斜边边长的平方。
比如经过(x,y)=(3,4)这点的切线斜率，经过该点的切线垂直于经过该点的半径。
假设我们不知道这个性质，或者想学习求任意曲线切线斜率通用方法，对于求曲线的切线斜率，我们可以从这里突破，我们把曲线不断放大。直至它和切线能几乎重合。

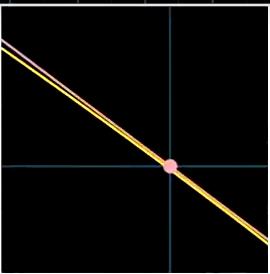
然后想像沿着曲线迈出微小的一步

我们把这一小步在y轴的变化叫做dy，在x轴的变化叫做dx

所以求切线的斜率就是沿曲线“上升除以前进”得到dy/dx
斜率公式：k= dy / dx

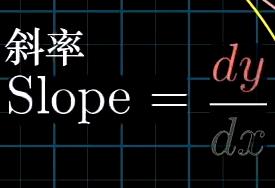
由于这里我们的曲线不是一个函数图像，所以我们不能单纯地对它求导，因为它不存在什么取值地微小变化所造成函数值地微小变化之类。

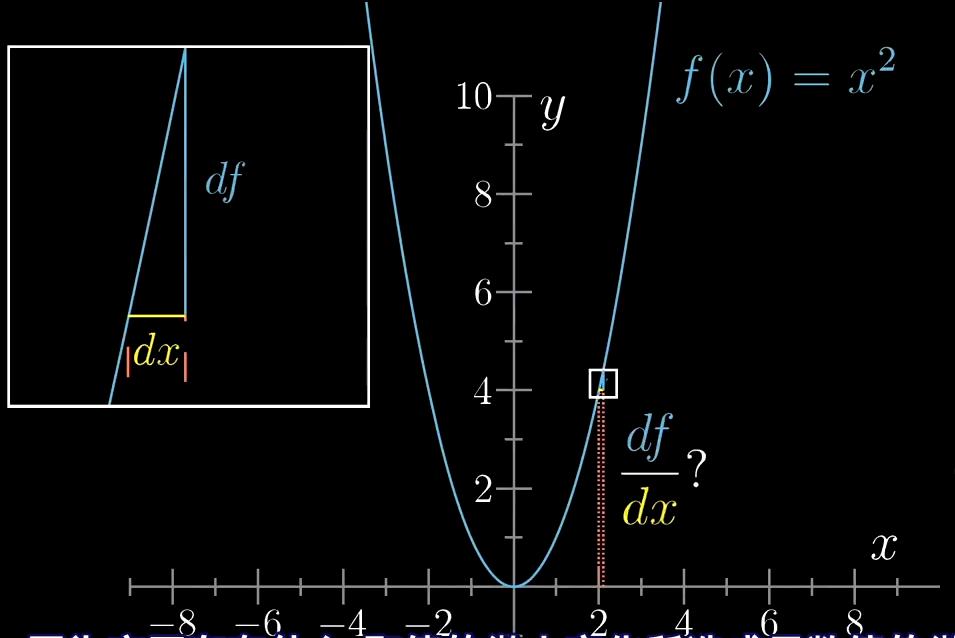
不存在输入一个x对应输出一个y，x和y同时由一个等式定义，而互相联系在一起，这种曲线就是“隐函数曲线”

隐函数

即满足某种关于变量x和y地性质，所有(x,y)点地集合

隐函数求导

我们要对表达式地两边同时求导

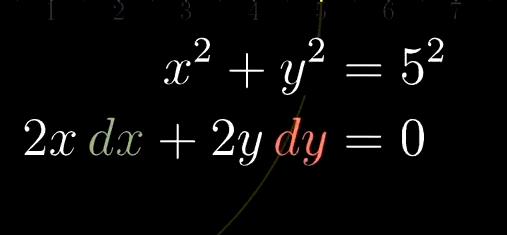
最终得到

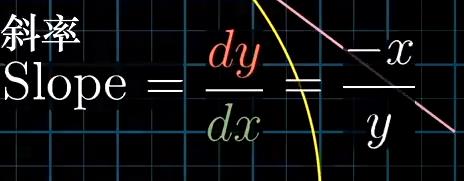
那么经过圆上(3,4)点的切线斜率就是-3/4

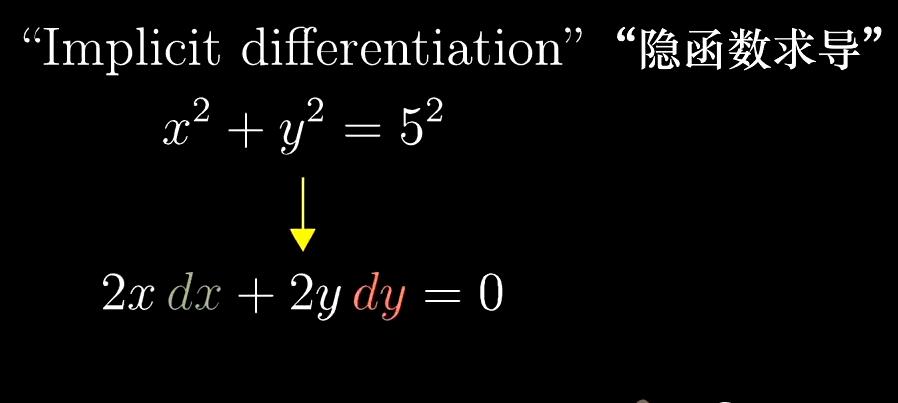
在此之前我们将讨论相关的变化率问题

梯子底端到墙角问题

有一个5m长的·梯子斜靠在墙上，现在梯子的顶端开始以1m/s的速度下滑，请问梯子底端离开墙角的速度是多少？

这个问题是由梯子顶端的离地高度所决定的，

梯子顶端离地的距离记作y(t)
底部距离墙角的距离记作x(t)
我们可以得到方程
x(t) ^ 2+y(t) ^ 2 = 5 ^ 2

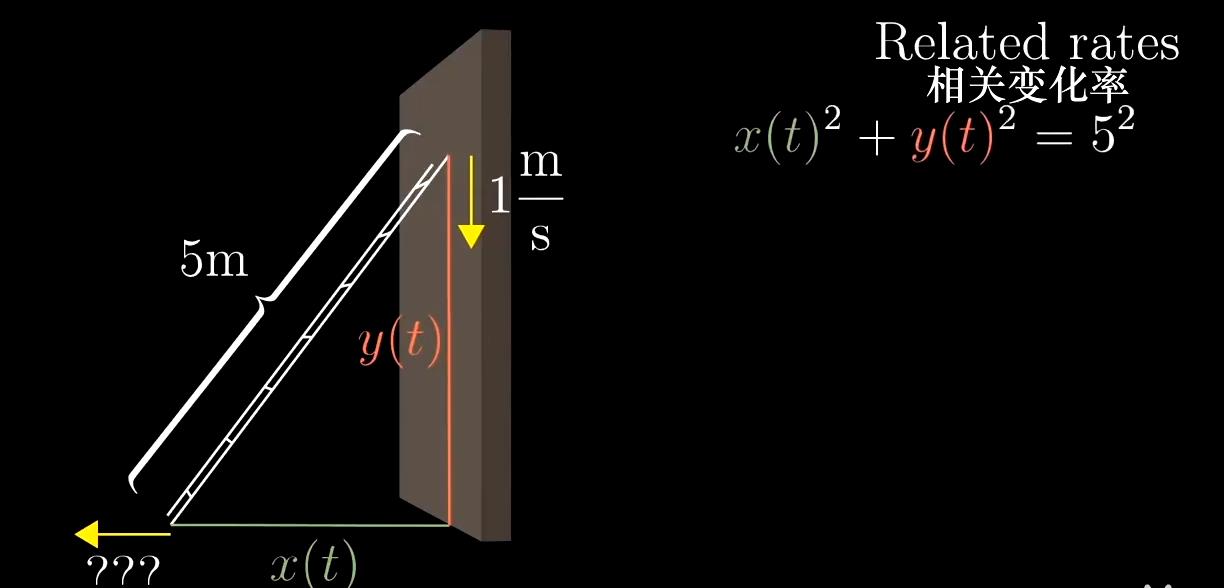
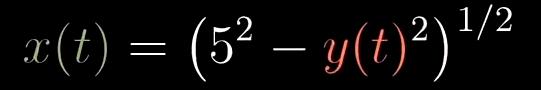
再对这个函数求导（链式法则）即可

其实我们可以对等式左边求导

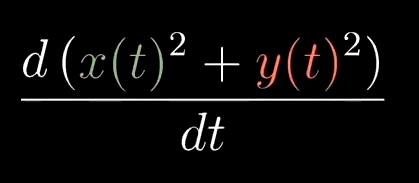
当dt秒后，整个表达式的值会变化多少？
5求导是0，因为常数是不随时间变化的，保持恒定的数

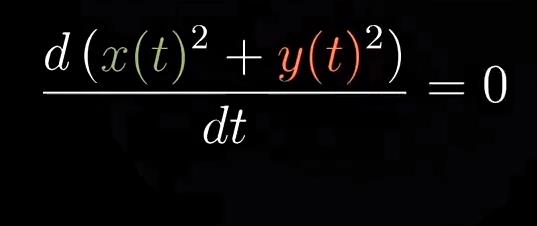
我们继续对左边的表达式求导。
x(t) ^2 的导数就变成了2* x(t)*（x的导数）

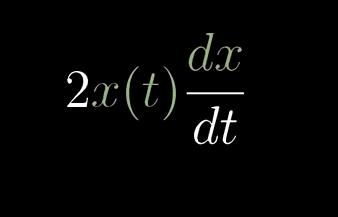
这里运用了链式法则

同理可得

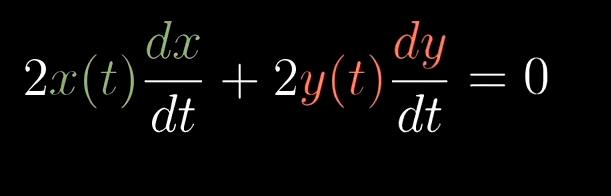
当运动开始，t=0，离地高度y(t)为4m，离墙距离x(t)为3m
又因为梯子开始以每秒1米的速度滑落，就表示导数dy/dt = -1 m/s,所以得到a=4/3米/秒

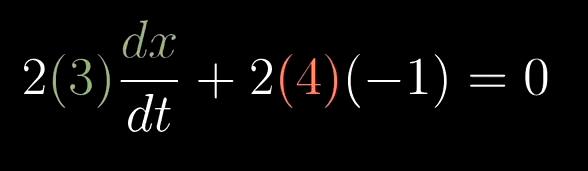
导数里的dx和dy看上去是悬空的


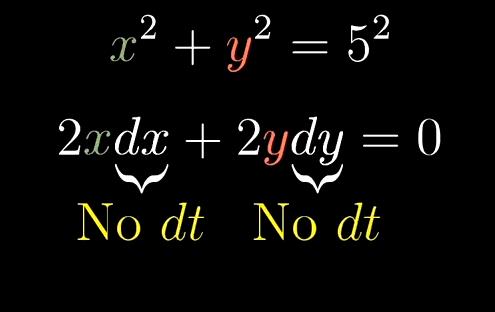
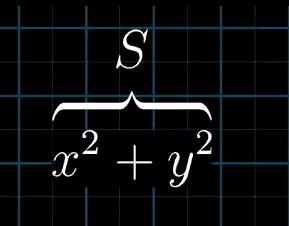
S实际上是取两个变量的函数，对于平面每点(x,y)它都会返回 一个值

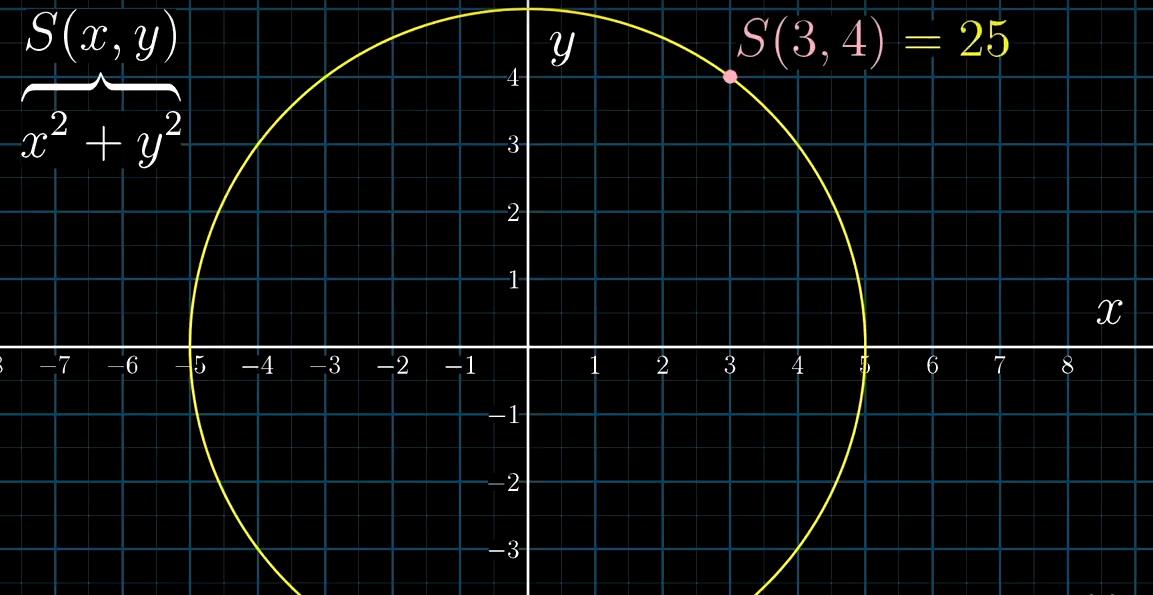
对于这个圆上所有点来讲，这个值就是25
点往圆外走，这个值就越大

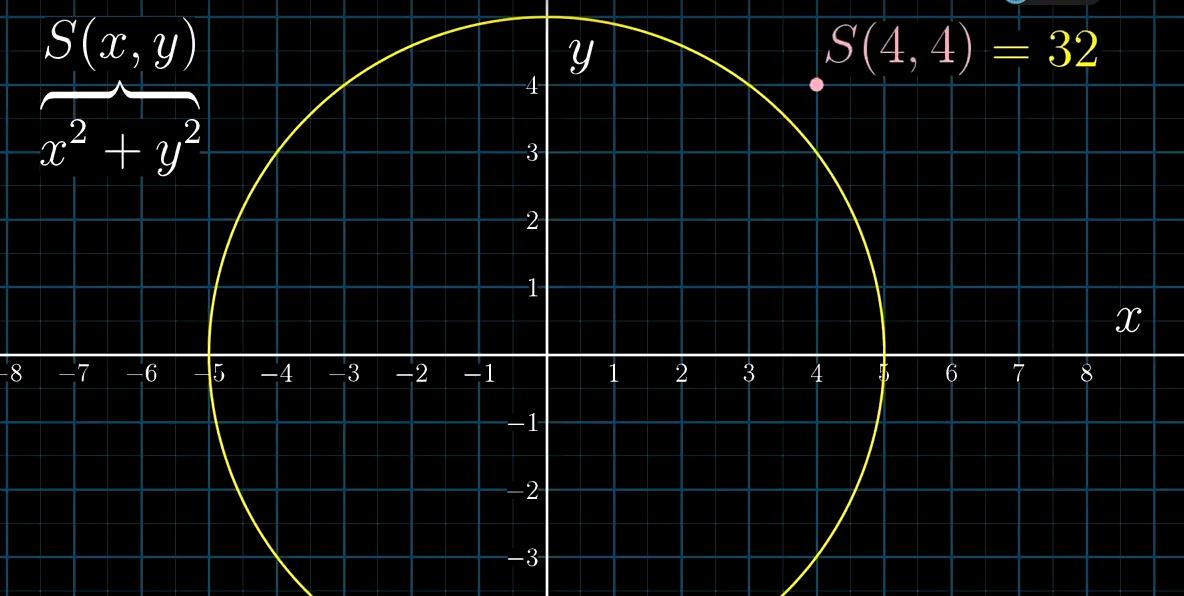
而(x,y)向圆心走，这值就越小。
那么我们对S求导。

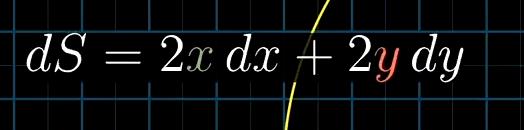
我们此时不需要关注这个变化还会不会留在圆上

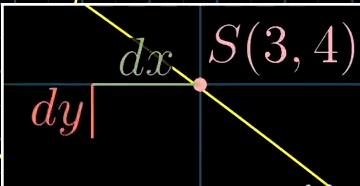
给S求导，就是再问”走这一步 S的值变化了多少？“
而这一步导致S产生的变化，就是我们的ds
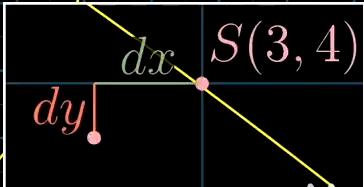
X=3 Y=4这点开始移动
假设移动的坐标变化量是
dx = -0.02 dy =-0.01

它实际上是函数值变化了多少。

对于所有求导而言，这只不过是一个近似值（Approximately）但这个近似值会随dx dy越来越小而越来越精确。如果我们把这每一小步都落在这个圆上的时候，你等就是需要S的值维持不变
S=25 那么 ds = 0
条件就是让表达式
2xdx+2ydy恒等于0

严格意义上来说，这个条件实际上是保证每一步都落在圆的一条切线上，而不是圆本身。
我们再看看另外一个例子
*sin(x)y ^2 =x

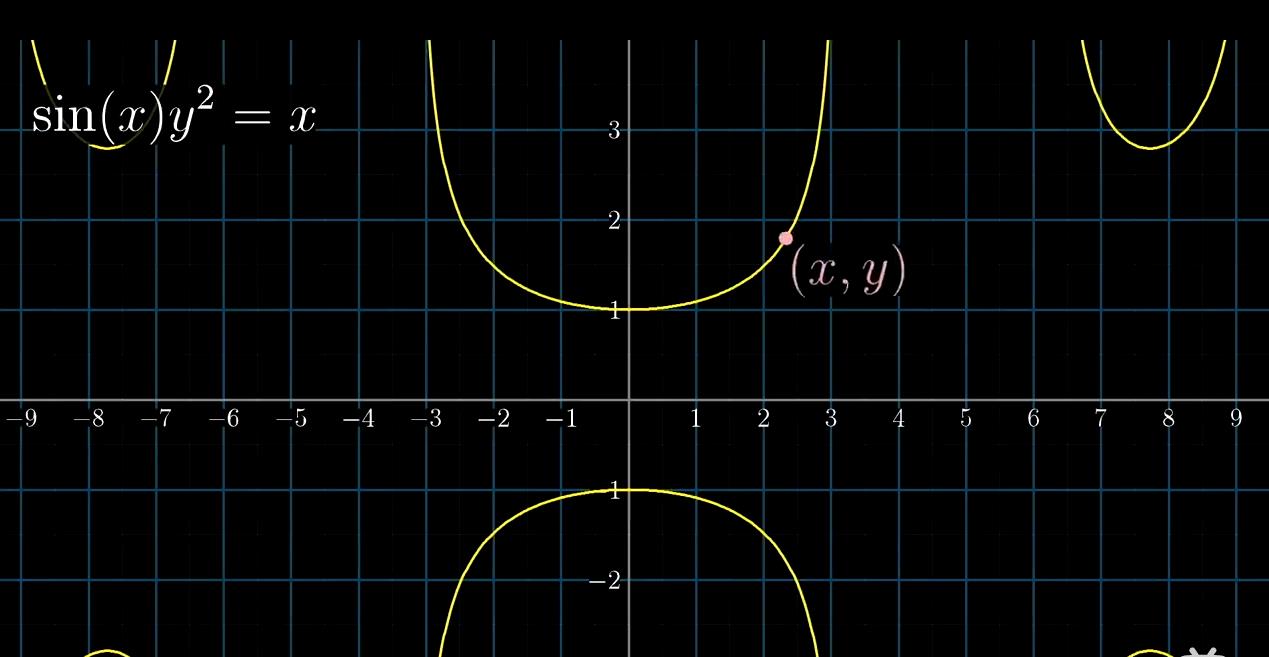
满足方程的正好等于x所有的集合

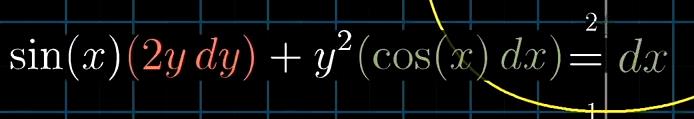
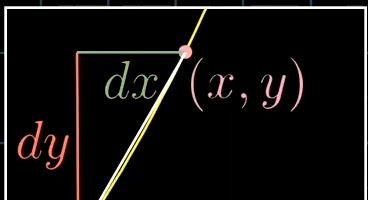
可以利用的隐函数求导方法

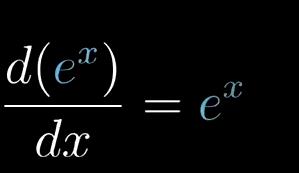
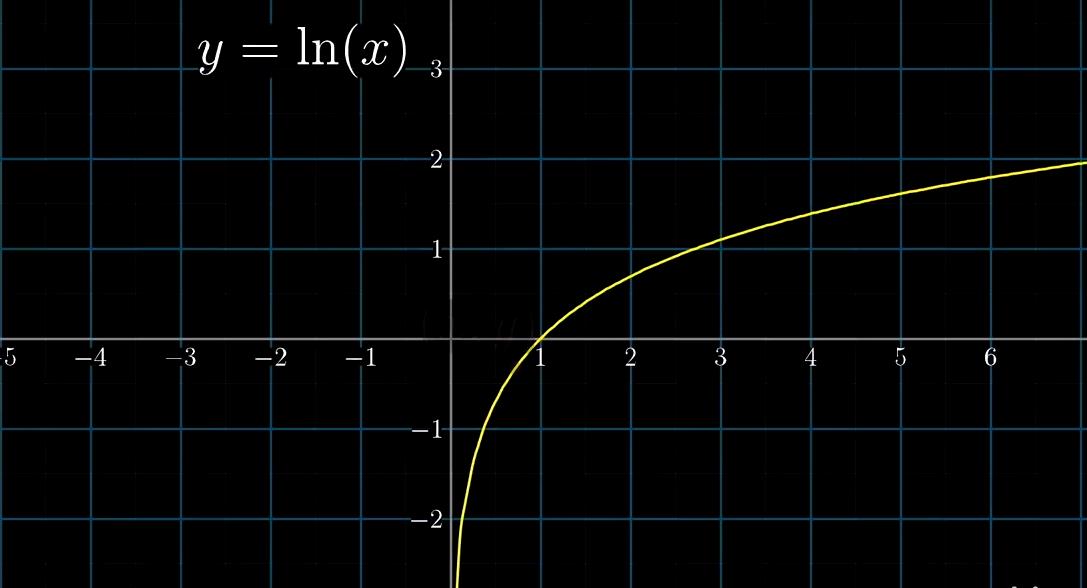
ln(x)函数可以看作是一个隐函数曲线


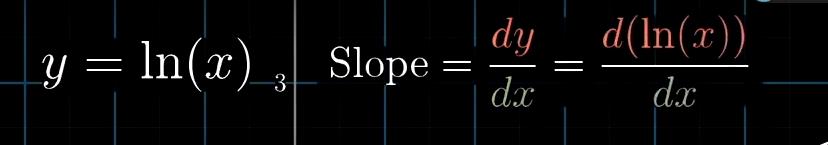
我们将他变作幂函数

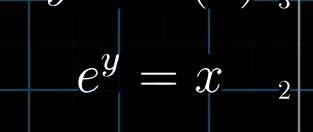
求e的多少次幂等于x

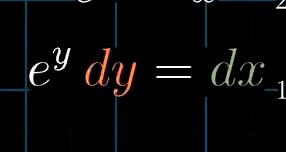
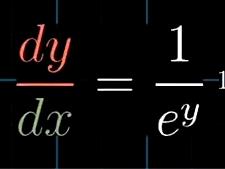
由上可以得到斜率就是1/x