深度学习项目拆解:识别猫的项目
Posted Debroon
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了深度学习项目拆解:识别猫的项目相关的知识,希望对你有一定的参考价值。
识别猫的项目
神经网络训练步骤
数据准备
数据下载:https://download.csdn.net/download/qq_41739364/22020268(都是一些动物的图片,像猫、狗、鸟)
import h5py # 数据是 H5 文件,需要 h5 模块
import matplotlib.pyplot as plt # 绘图库,之后会查看图片
import numpy as np
train_dataset = h5py.File('./我的数据集/train_catvnoncat.h5','r') # 读取训练集(创建了一个字典格式的对象)
test_dataset = h5py.File('./我的数据集/test_catvnoncat.h5','r') # 读取测试集(创建了一个字典格式的对象)
# 因为对象是字典,所以用数据之前,还需要键名
for key1 in train_dataset.keys():
print( train_dataset[key1].name ) # 查看训练集键名(标签类别list_classes、图片特征train_set_x、图片标签train_set_y)
for key2 in test_dataset.keys():
print( test_dataset[key2].name ) # 查看测试集键名(标签类别list_classes、图片特征test_set_x、图片标签test_set_y)
train_set_x = np.array(train_dataset["train_set_x"][:]) # 通过键名,访问所有数据,并保存到数组里
train_set_y = np.array(train_dataset["train_set_y"][:]) # 通过键名,访问所有数据,并保存到数组里
test_set_x = np.array(test_dataset["test_set_x"][:]) # 通过键名,访问所有数据,并保存到数组里
test_set_y = np.array(test_dataset["test_set_y"][:]) # 通过键名,访问所有数据,并保存到数组里
print("train_set_x.shape = ",train_set_x.shape) # 查看训练集数组维度( (209, 64, 64, 3) 意思是,209张图片,尺寸是 64*64*3,64x64x3 = 12288个特征 )
print("test_set_x.shape = ",test_set_x.shape) # 查看测试集数组维度( (50, 64, 64, 3) 意思是,50张图片,尺寸是 64*64*3,64x64x3 = 12288个特征 )
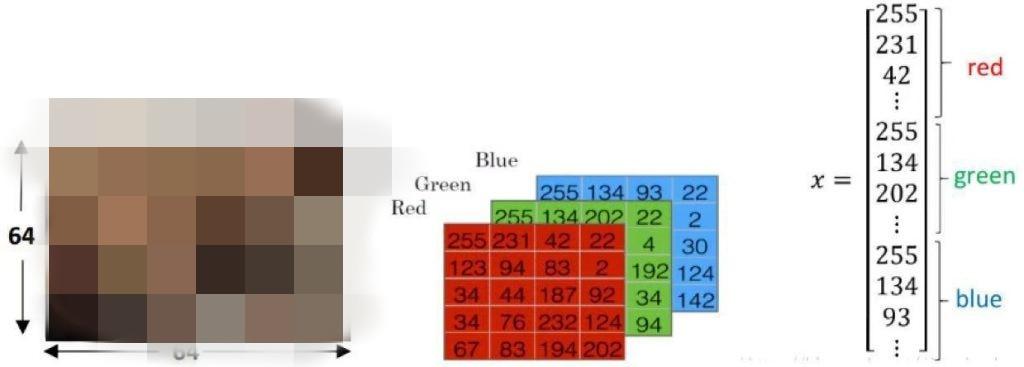
一张图片是一个三维数组 64 * 64 * 3,64 是长和宽,3 是 RGB 三个通道,因为这是一张彩色图片,每个像素点必须用三个数来代表,一张图片就要用 1 万多个数来描述。
209 张图片,是一个四维数组 209 * 64 * 64 * 3,而神经元的输入是二维的列矩阵 209 * 1,所以我们要转换一下。
# 图片特征 xx_set_x:(209, 64, 64, 3) -> (12288,209)
train_set_x = train_set_x.reshape(train_set_x.shape[0], -1).T # (209, 64, 64, 3) 变成 (12288,209)
test_set_x = test_set_x.reshape(test_set_x.shape[0], -1).T # (209, 64, 64, 3) 变成 (12288,50)
# 图片标签 xx_set_y:(209,) -> (1,209)
train_set_y = train_set_y.reshape(1,train_set_y.shape[0]) # (209,) 变成 (1,209)
test_set_y = test_set_y.reshape(1,test_set_y.shape[0]) # (50,) 变成 (1,50)
# P.S. 标签类别list_classes 非0即1,0即非猫,1即是猫。
最后归一化,我们要把数据经过处理后使之限定在一定的范围内。比如通常限制在区间 [0, 1]。
train_set_x = train_set_x/255.0
test_set_x = test_set_x/255.0
# 除以255.0是为了使数据的取值范围在sigmoid激励函数的取值范围内
#【注:灰度图像素取值为0-255,相除后取值在0-1之间,符合激励函数的输出范围】
好,现在我们把数据准备这部分封装为一个函数。
import h5py # 数据是 H5 文件,需要 h5 模块
import matplotlib.pyplot as plt # 绘图库,之后会查看图片
import numpy as np
def load_dataset():
# 创建文件对象
train_dataset = h5py.File('./我的数据集/train_catvnoncat.h5','r')
test_dataset = h5py.File('./我的数据集/test_catvnoncat.h5','r')
# 读取数据
train_set_x = np.array(train_dataset["train_set_x"][:])
train_set_y = np.array(train_dataset["train_set_y"][:])
test_set_x = np.array(test_dataset["test_set_x"][:])
test_set_y = np.array(test_dataset["test_set_y"][:])
# 查看第 110 张图片
plt.figure(figsize=(2,2))
plt.imshow(train_set_x[110])
plt.show()
# 变化维度以适应神经网络输入
train_set_x = train_set_x.reshape(train_set_x.shape[0],-1).T
test_set_x = test_set_x.reshape(test_set_x.shape[0],-1).T
train_set_y = train_set_y.reshape(1,train_set_y.shape[0])
test_set_y = test_set_y.reshape(1,test_set_y.shape[0])
# 数据归一化
train_set_x = train_set_x/255.0
test_set_x = test_set_x/255.0
return train_set_x,train_set_y,test_set_x,test_set_y
if __name__ == '__main__':
train_set_x, train_set_y, test_set_x, test_set_y = load_dataset()
# 加载数据
定义神经网络结构
加载数据后,定义神经网络结构。
if __name__ == '__main__':
load_dataset()
# 加载数据
fc_net = [12288, 4, 3, 2, 1]
# 用数组定义神经网络结构,输入层(12288个神经元)->第1层->第2层->第3层->第4层->a,有多少层、一层多少神经元,都取决于工程师的直觉,差不多就行
# 输出值a,a>0.5 ? 1:0
解析神经网络、初始化参数(w、b)
定义神经网络结构之后,解析神经网络
if __name__ == '__main__':
train_set_x, train_set_y, test_set_x, test_set_y = load_dataset()
# 加载数据
fc_net = [12288, 4, 3, 2, 1]
# 用数组定义神经网络结构,输入层(12288个神经元)->第1层->第2层->第3层->第4层->a
# 输出值a,a>0.5 ? 1:0
parameters = init_parameters(fc_net)
# 解析神经网络,初始化权值
现在我们来实现初始化权值 init_parameters 的实现。
# 初始化参数
def init_parameters(fc_net):
parameters = {}
# 定义一个字典,存放参数矩阵W1,b1,W2,b2,W3,b3,W4,b4
Layer_num = len(fc_net)
# 神经网络的层数,通过获取数组长度可得
for L in range(1, Layer_num): # 遍历层数,从第一层开始,但忽略输入层(第 0 层)
parameters["W"+str(L)] = np.random.randn(fc_net[L], fc_net[L-1])*0.01
# 从标准正态分布中(取值范围[-3,3])选取值,为方便激活函数(取值范围[-1,1]),乘以0.01后,再赋值给创建的键值对(W1、W2、W3···)
parameters["b"+str(L)] = np.zeros((fc_net[L], 1))
for L in range(1, Layer_num):
print("W"+str(L)+" = ", parameters["W"+str(L)].shape)
print("b"+str(L)+" = ", parameters["b"+str(L)].shape)
return parameters
输入数据,前向传播
if __name__ == '__main__':
train_set_x, train_set_y, test_set_x, test_set_y = load_dataset()
# 加载数据
fc_net = [12288, 4, 3, 2, 1]
# 输入层->第1层->第2层->第3层->第4层->a
# 输出值a,a>0.5 ? 1:0
parameters = init_parameters(fc_net)
# 初始化权值
AL, cache = forward_pass(train_set_x, parameters, active_func = "tanh")
# 最后一层激活值AL = train_set_x 输入数据、parameters W、b 保存位置、激活函数是 tanh
现在我们来实现激活函数。
def sigmoid(Z):
return 1 / (1 + np.exp(-Z))
def tanh(Z):
return np.tanh(Z)
def ReLU(Z):
return np.maximum(0,Z)
再来实现前向传播 forward_pass。
def forward_pass(A0, parameters, active_func = "ReLU"):
Layer_num = len(parameters) // 2 # 因为 parameters 是由 W、b 组成,所以除 2
A = A0
cache = {} # 缓存 A 的字典
cache["A0"] = A0 # 先缓存A0
for L in range(1,Layer_num):
A_prev = A
Z = np.dot(parameters["W"+str(L)],A_prev) + parameters["b"+str(L)] # Z = WX + b
cache["Z"+str(L)] = Z # 缓存Z1 Z2 Z3 Z4
if active_func == "sigmoid":
A = sigmoid(Z) # sigmoid函数,适合用于深度网络
elif active_func == "tanh":
A = tanh(Z) # tanh函数激活
else:
A = ReLU(Z) # 1~3层用 ReLU 函数激活
cache["A"+str(L)] = A # 继续缓存 A1 A2 A3 A4
# 最末层采用sigmoid函数激活
ZL = np.dot(parameters["W" + str(Layer_num)], A) + parameters["b" + str(Layer_num)] # 1,2 2,209
cache["Z" + str(Layer_num)] = ZL # 缓存最末层的Z4
AL = sigmoid(ZL) # sigmoid函数激活
cache["A"+str(Layer_num)]=AL # 继续缓存最末层的A4
return AL, cache
对比《深度学习食用指南》识别猫的项目,这里多了一个要缓存 A,这是为啥?
其实是一种算法策略:空间换时间,因为前向传播过程如下所示:
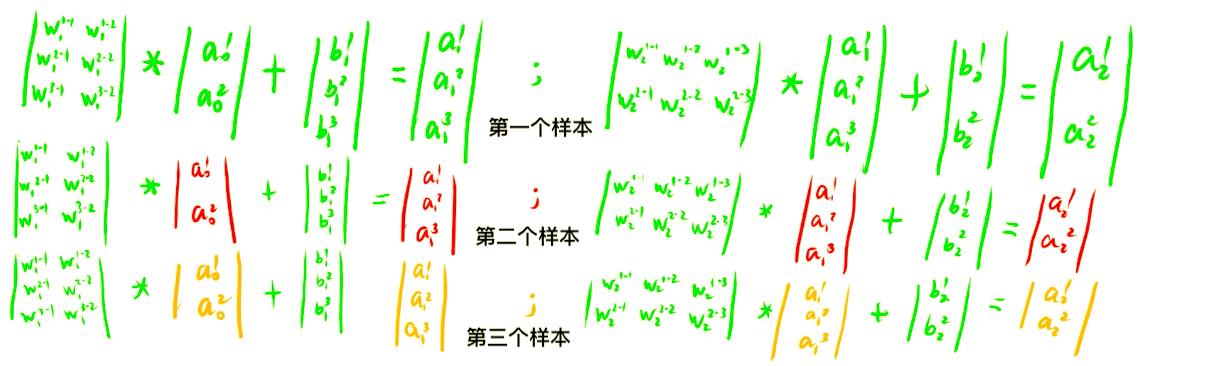
一般的前向传播过程,我们是一个一个计算的,处理完一个样本再处理下一个样本,等所有样本都处理完了,才能反向传播,求参数的梯度。
能不能同时计算呢?
- a 0 a_{0} a0 是输入样本,是不需要计算就可以得到的,我们把上面的 a 0 a_{0} a0 堆叠起来。
- b i b_{i} bi 也堆叠起来,后面的输出值 a i a_{i} ai 也堆叠起来。
- w i w_{i} wi 矩阵也移过来。
 就把多个样本中用 for 循环实现的多步串行计算,改成了用矩阵实现的一步完成的并行计算。
就把多个样本中用 for 循环实现的多步串行计算,改成了用矩阵实现的一步完成的并行计算。
得到本轮迭代的损失值
if __name__ == '__main__':
train_set_x, train_set_y, test_set_x, test_set_y = load_dataset()
# 加载数据
fc_net = [12288, 4, 3, 2, 1]
# 输入层->第1层->第2层->第3层->第4层->a
# 输出值a,a>0.5 ? 1:0
parameters = init_parameters(fc_net)
# 初始化权值
AL,cache= forward_pass(train_set_x, parameters)
# 最后一层激活值AL = train_set_x 输入数据、parameters W、b 保存位置
cost = compute_cost(AL, train_set_y)
使用损失函数计算,预测值与标签值(真实值)的差距。
def compute_cost(AL, Y):
m = Y.shape[1] # Y =(1,209)
cost = (1/m)*np.sum((1/2)*(AL-Y)*(AL-Y)) # 代价函数
return cost
求最末层误差,反向传播计算各层梯度
if __name__ == '__main__':
train_set_x, train_set_y, test_set_x, test_set_y = load_dataset()
# 加载数据
fc_net = [12288, 4, 3, 2, 1]
# 输入层->第1层->第2层->第3层->第4层->a
# 输出值a,a>0.5 ? 1:0
parameters = init_parameters(fc_net)
# 初始化权值
AL,cache= forward_pass(train_set_x, parameters)
# 最后一层激活值AL = train_set_x 输入数据、parameters W、b 保存位置
cost = compute_cost(AL, train_set_y)
gradient = backward_pass(AL, parameters, cache, train_set_y)
# 反向传播计算梯度
我们来实现反向传播 backward_pass。
def backward_pass(AL, parameters, cache, Y):
m = Y.shape[1] # 样本总数
gradient = {} # 保存各层参数梯度的字典
Layer_num = len(parameters) // 2
dZL = (AL-Y)*(AL*(1-AL)) # 获取最末层误差信号 dZL.shape = (1,209)
gradient["dW"+str(Layer_num)] = (1/m)*np.dot(dZL,cache["A"+str(Layer_num-1)].T)
gradient["db"+str(Layer_num)] = (1/m)*np.sum(dZL,axis=1,keepdims = True)
for L in reversed(range(1,Layer_num)): # 遍历[3,2,1],其中reversed函数[1,2,3]颠倒为[3,2,1]
dZL = np.dot(parameters["W"+str(L+1)].T,dZL)*(AL*(1-AL))
gradient["dW"+str(L)] = (1/m)*np.dot(dZL,cache["A"+str(L-1)].T)
gradient["db"+str(L)] = (1/m)*np.sum(dZL,axis=1,keepdims = True)
return gradient
根据各层的w、b梯度,使用梯度下降更新一次参数
if __name__ == '__main__':
train_set_x, train_set_y, test_set_x, test_set_y = load_dataset()
# 加载数据
fc_net = [12288, 4, 3, 2, 1]
# 输入层->第1层->第2层->第3层->第4层->a
# 输出值a,a>0.5 ? 1:0
parameters = init_parameters(fc_net)
# 初始化权值
AL,cache= forward_pass(train_set_x, parameters)
# 最后一层激活值AL = train_set_x 输入数据、parameters W、b 保存位置
cost = compute_cost(AL, train_set_y)
gradient = backward_pass(AL, parameters, cache, train_set_y)
# 反向传播计算梯度
iterations = 500
LearnRate = 0.01
costs = []
# 保存我们每次迭代计算得到的代价值
parameters = update_parameters(gradient, parameters, LearnRate)
# 根据梯度更新一次参数
得到梯度后,实现梯度下降。
def update_parameters(gradient,parameters,LearnRate):
# w : =w-r*dw、b := b-r*db
Layer_num = len(parameters) // 2
for L in range(1,Layer_num+1):
parameters["W"+str(L)] = parameters["W"+str(L)] - LearnRate*gradient["dW"+str(L)]
parameters["b"+str(L)] = parameters["b"+str(L)] - LearnRate*gradient["db"+str(L)]
return parameters
重复以上步骤,直到损失值低于设定阈值,模型收敛
if __name__ 以上是关于深度学习项目拆解:识别猫的项目的主要内容,如果未能解决你的问题,请参考以下文章
深度学习基于卷积神经网络(tensorflow)的人脸识别项目