Leetcode——三角形最小路径和

Posted 2021-09-25 Yawn,

1. 三角形最小路径和

（1）递归

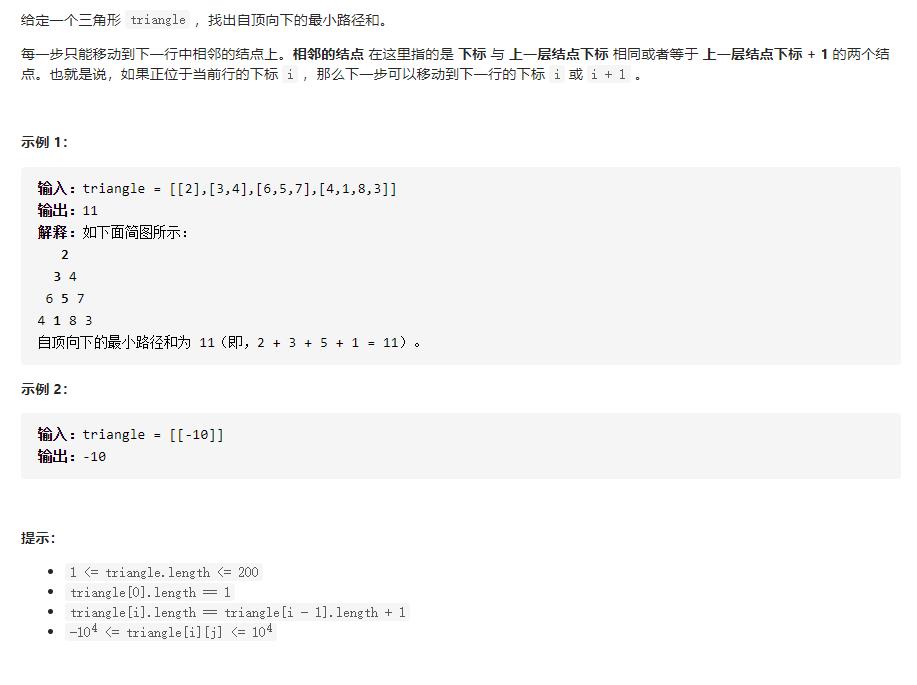
每次只能移动到下一行中的相邻结点，求从顶点到底边的最小路径和。

[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
相邻结点：与(i, j) 点相邻的结点为 (i + 1, j) 和 (i + 1, j + 1)。

若定义 f(i, j)f(i,j) 为 (i, j)(i,j) 点到底边的最小路径和，则易知递归求解式为:

f(i,j) = min(f(i + 1,j), f(i + 1, j + 1)) + triangle[i][j]

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        return  dfs(triangle, 0, 0);
    }

    private int dfs(List<List<Integer>> triangle, int i, int j) {
        if (i == triangle.size()) {
            return 0;
        }
        return Math.min(dfs(triangle, i + 1, j), dfs(triangle, i + 1, j + 1)) + triangle.get(i).get(j);
    }
}

（2）递归优化

• 直接递归暴力搜索会有大量重复计算，所以会超时
• 在解法一的基础上，定义了二维数组进行记忆化。
• 时间复杂度：O(N^2) ，N 为三角形的行数。
  空间复杂度：O(N^2)，NN 为三角形的行数。

class Solution {
	//使用Integer数组是为了判断数组某个位置是否存在值
    Integer[][] memo;
    public int minimumTotal(List<List<Integer>> triangle) {
        memo = new Integer[triangle.size()][triangle.size()];
        return  dfs(triangle, 0, 0);
    }

    private int dfs(List<List<Integer>> triangle, int i, int j) {
        if (i == triangle.size()) {
            return 0;
        }
        if (memo[i][j] != null) {
            return memo[i][j];
        }
        return memo[i][j] = Math.min(dfs(triangle, i + 1, j), dfs(triangle, i + 1, j + 1)) + triangle.get(i).get(j);
    }
}

 

（3）DP （自上而下）

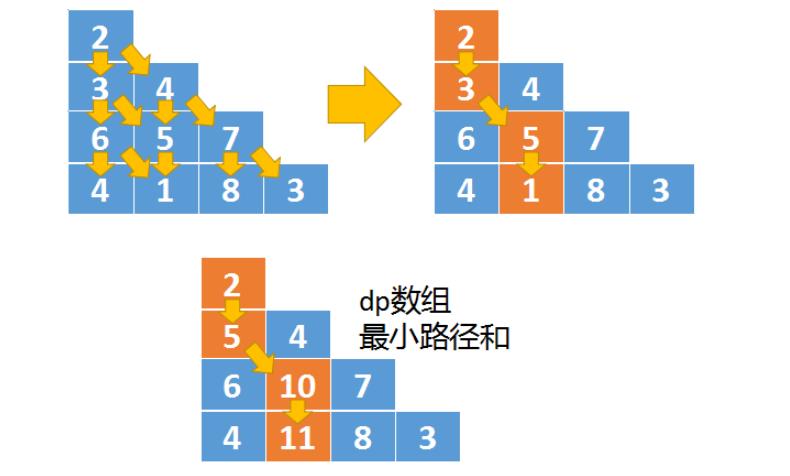
对于三角形中任意一个位置triangle[i][j]，只有两个值能移动到这个位置
分别是triangle[i-1][j-1]，以及triangle[i-1][j]。

但是注意了，自上而下推导时，有两个特例

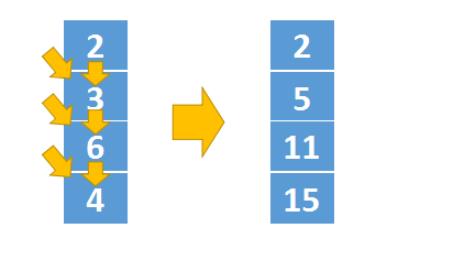
第一列计算的时候，如果用dp[i-1][j-1]获取斜上方值时会出现下标越界。从上图中我们也可以发现，实际上第一列计算的时候，它只有一条转移路径，我们需要单独处理

dp[i][0] = dp[i-1][0] + triangle[i][0]

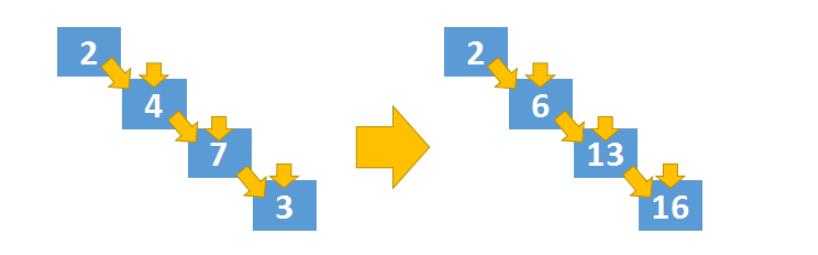
最后一列也需要单独计算(斜边)，这条斜边也是只有一条转移路径，同样也需要单独处理，其计算公式如下:

dp[i][j] = dp[i-1][j-1] + triangle[i][j]

最后代码：

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        // 特例单独处理
        if (triangle == null || triangle.size() == 0) {
            return 0;
        }
        int n = triangle.size();
        int m = triangle.get(n - 1).size();       //get获取最后一行的元素，并求长度（三角形最后一行元素最大）


        //创建n*m的二维数组
        int[][] dp = new int[n][m];
        //初始化dp[0][0]
        dp[0][0] = triangle.get(0).get(0);
        //第一列需要单独计算
        for (int i = 1; i < n; ++i) {
            dp[i][0] = dp[i - 1][0] + triangle.get(i).get(0);
        }
        for (int i = 1; i < n; ++i) {
            int j = 1;
            //注意计算的是三角形每一行的长度都不同
            //最后一列需要单独计算(斜边)，所以是从遍历的个数是size()-1
            while (j < triangle.get(i).size()-1) {
                //状态转移公式
                dp[i][j] = Math.min(dp[i-1][j-1],dp[i-1][j]) + triangle.get(i).get(j);
                ++j;
            }

            //三角形斜边需要单独计算
            dp[i][j] = dp[i-1][j-1] + triangle.get(i).get(j);
        }

        //最后一行保存了每条路径的计算结果，对最后一行数组求min即为最终结果
        int min = dp[n - 1][0];
        for (int i = 0; i < dp[n - 1].length; i++) {
            min = Math.min(dp[n - 1][i], min);
        }
        return min;
    }
}

（4）DP（自下而上）

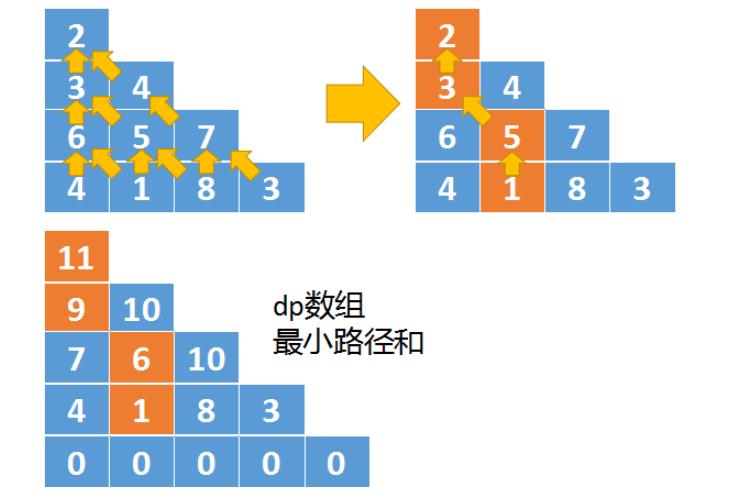
• 自下而上推导时，结果保存在第一行第一列中，因为三角形第一行只有一个元素，所以最终结果就保存在dp[0][0]中
• 此外dp数组跟自上而下比也有些变化，这里的dp数组是原始数组的行数+1
• 以自下而上的角度看，三角形中任意一个位置triangle[i][j]，只有两个值能移动到这个这里
  分别是triangle[i+1][j+1]，以及triangle[i+1][j]，如下图所示
  
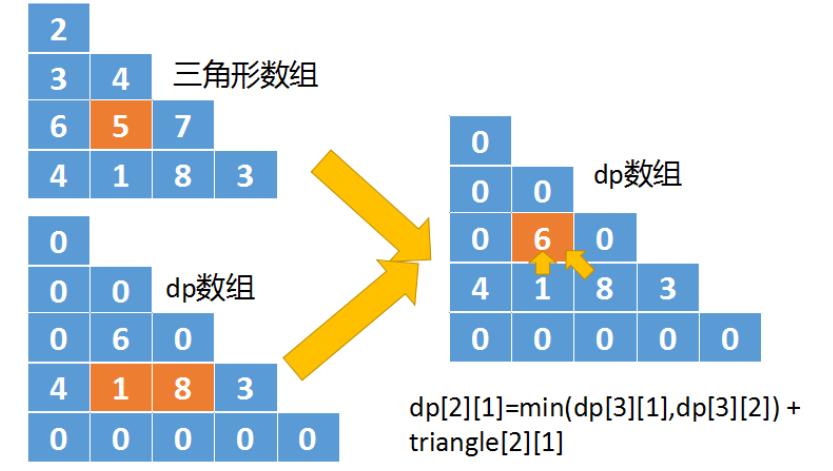
  其dp转移公式为：

dp[i][j] = min(dp[i+1][j+1],dp[i+1][j]) + triangle[i][j]

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        if (triangle == null || triangle.size() == 0) {
            return 0;
        }

        int n = triangle.size();
        int m = triangle.get(n - 1).size();
        //之所以以要多加一行，是因为状态转移公式变化导致的，为了处理一些边界条件所以增加了一行
        int[][] dp = new int[n + 1][m + 1];

        //自下而上推导
        for (int i = n - 1; i >= 0; --i) {

            //对于三角形的每一行，从右向左计算
            for (int j = triangle.get(i).size() - 1; j >= 0; j--) {
                dp[i][j] = Math.min(dp[i+1][j+1], dp[i+1][j]) + triangle.get(i).get(j);
            }
        }
        //最终结果就保存在第一行第一列中
        return dp[0][0];
    }
}

（5）DP空间优化

• 用二维数组计算 dp[i][j] 时只用到了 dp[i+1][j+1] 和 dp[i+1][j]
• 也就是说这是一个滚动更新的过程，我们只用到了上下两行数据
• 求dp[i][j]时只需要dp[i+1]这一行的数据即可，dp[i+2]，dp[i+3]…这些都不需要了。
• 于是我们可以创建一个一维数组，其长度为三角形列数+1
  
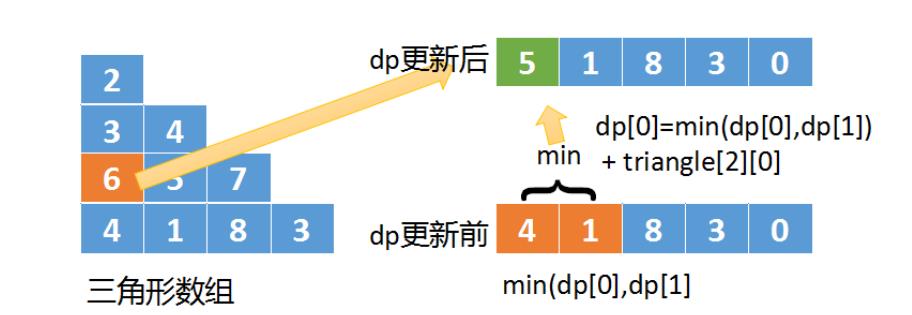
• 如上图所示，我们还是按照自下而上的方式，但这次的dp数组改成一维的了
• 计算triangle[2][0]的最小路径为:
  triangle[2][0] + min(dp[0],dp[1])
• 之后将结果5保存到dp[0]中
• 所以一维数组的状态转移方程为:

dp[j] = min(dp[j],dp[j+1]) +triangle[i][j]

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        if (triangle == null || triangle.size() == 0) {
            return 0;
        }
        int n = triangle.size();
        int m = triangle.get(n - 1).size();
        
        //申请的dp数组为最长列+1
        int[] dp = new int[m+1];
        for (int i = n-1; i >= 0; --i) {
            //从左到右的方式计算
            for (int j = 0; j < triangle.get(i).size(); ++j) {
                dp[j] = Math.min(dp[j],dp[j+1]) + triangle.get(i).get(j);
            }
        }

        //dp数组的第一个元素即为最终结果
        return dp[0];
    }
}