数据结构之堆
Posted 小倪同学 -_-
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构之堆相关的知识,希望对你有一定的参考价值。
堆的概念及结构

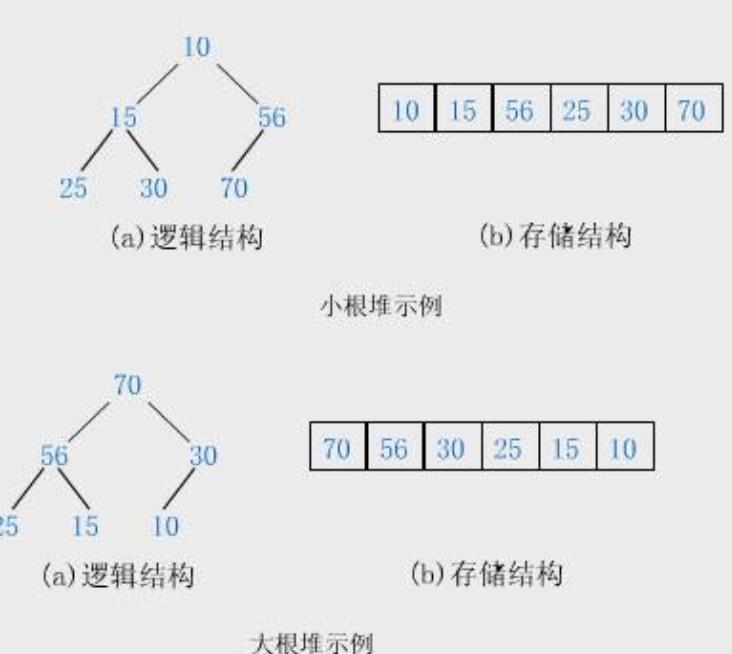
定义堆
实现堆的功能首先要定义堆的结构体
typedef int HPDataTpye;
typedef struct Heap
{
HPDataTpye* a; //存储数据
int size; //保存元素个数
int capacity; //存储容量
}HP;
堆的初始化
思路:
- 先开辟一块空间,将传入的数据存放到堆的结构体中
- 将堆中数据建堆排序
- 将堆结构中容量,元素个数初始化
开辟空间不难,那么如何建堆呢?
这里有两种思路,一是从上往下调整,二是从下往上调整
思路一:
从上往下调整
将传入的结点当做父节点,比较其两个子节点,将子节点与父节点比较,如果不满足堆的条件就交换,并将原先子节点的位置当成父节点,重复上述操作。如果满足堆的条件就结束操作。(注意:该程序是建立在左右子树都为大堆基础上的)

代码如下
void Swap(int* px, int* py)
{
int tmp = *px;
*px = *py;
*py = tmp;
}
// 条件:左右子树都是小堆/大堆
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
// 选出左右孩子中小 or 大的那个
if (child + 1 < n && a[child + 1] < a[child])
{
++child;
}
// 1、如果小 or 大的孩子比父亲小 or 大,则交换,继续往下调整
// 2、如果小 or 大 的孩子比父亲大 or 小,则结束调整
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
思路二:
从下往上建
将传入的结点当做子节点,找到其父结点并与之比较,不满足堆的条件就交换,并将原父结点的位置当成子节点重复之前操作。满足堆的条件则退出程序。(注意:该程序建立在除传入的子节点外,其余结点都满足堆条件基础上的)

代码实现
void Swap(int* px, int* py)
{
int tmp = *px;
*px = *py;
*py = tmp;
}
void AdjustUp(int* a, int child)
{
int parent = (child - 1) / 2;
//while (parent >= 0) 不对的 parent不会小于0
while (child > 0)
{
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
初始化总体代码
void Swap(int* px, int* py)
{
int tmp = *px;
*px = *py;
*py = tmp;
}
// 条件:左右子树都是小堆/大堆
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
// 选出左右孩子中小 or 大的那个
if (child + 1 < n && a[child + 1] < a[child])
{
++child;
}
// 1、如果小 or 大的孩子比父亲小 or 大,则交换,继续往下调整
// 2、如果小 or 大 的孩子比父亲大 or 小,则结束调整
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void AdjustUp(int* a, int child)
{
int parent = (child - 1) / 2;
//while (parent >= 0) 不对的 parent不会小于0
while (child > 0)
{
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void HeapInit(HP* php, HPDataTpye* a, int n)
{
assert(php);
//开辟空间
php->a = (HPDataTpye*)malloc(sizeof(HPDataTpye)*n);
if (php->a == NULL)
{
printf("malloc fail\\n");
exit(-1);
}
//转移数据
memcpy(php->a, a, sizeof(HPDataTpye)*n);
//建堆排序
for (int i = (n - 2) / 2; i >= 0; i--)
{
AdjustDown(php->a, n, i);
}
php->capacity = n;
php->size = n;
}
插入数据
思路:
- 检查是否满容量,满了就扩容
- 插入数据,并将size+1
代码:
void HeapPush(HP* php, HPDataTpye x)
{
assert(php);
if (php->capacity == php->size)
{
HPDataTpye* tmp = (HPDataTpye*)realloc(php->a, 2 * php->capacity*sizeof(HPDataTpye));
if (php->a == NULL)
{
printf("realloc fail\\n");
exit(-1);
}
php->capacity *= 2;
}
php->a[php->size] = x;
php->size++;
AdjustUp(php->a, php->size - 1);
}
判空
思路:
判空只需判断其元素个数是否为0即可
代码:
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
删除堆顶的数据
思路:
- 先判空处理
- 将堆顶数据和最后一个叶结点数据交换
- 从上往下调整堆

代码:
void HeapPop(HP* php)
{
assert(php);
assert(!HeapEmpty(php));
//交换头尾数据
Swap(&php->a[0], &php->a[php->size - 1]);
php->size--;
AdjustDown(php->a, php->size, 0);
}
获取堆顶数据
思路:
先判空,再取出堆顶数据
代码:
HPDataTpye HeapTop(HP* php)
{
assert(php);
assert(!HeapEmpty(php));
return php->a[0];
}
获取元素个数
直接返回size
int HeapSize(HP* php)
{
assert(php);
return php->size;
}
打印
void HeapPrint(HP* php)
{
for (int i = 0; i < php->size; i++)
{
printf("%d ", php->a[i]);
}
printf("\\n");
}
销毁堆
将开辟的空间释放,并将size,capacity赋值为0
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);
php->a = NULL;
php->capacity = php->size = 0;
}
Topk问题
问:如何取出一组数据中最大的前K个值
有人会想到把所有数据建大堆,取出堆顶数据再删除该数据,重复操作K次
操作如下
void TestHeap()
{
int a[] = { 27, 37, 28, 18, 19, 34, 65, 4, 25, 49, 15 };
HP hp;
HeapInit(&hp, a, sizeof(a) / sizeof(int));
HeapPrint(&hp);
printf("\\n");
int k = 0;
scanf("%d", &k);
printf("找出数组中最小的前%d个:", k);
while (!HeapEmpty(&hp)&&k--)
{
printf("%d ", HeapTop(&hp));
HeapPop(&hp);
}
printf("\\n");
}

如果该组数据个数为一万,十万呢?
这时用该方法不但耗费时间而且十分耗内存,那有没有时间复杂符度较小的用堆实现的方法呢?
答案是有的,那就是Topk算法
Topk基本思路如下:
- 用数据集合中前K个元素来建堆
求前k个最大的元素,则建小堆
求前k个最小的元素,则建大堆 - 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
代码实现
void PrintTopK(int* a, int n, int k)
{
HP hp;
HeapInit(&hp, a, k);
for(int i = k; i < n; i++)
{
if (a[i]>HeapTop(&hp))
{
HeapPop(&hp);
HeapPush(&hp, a[i]);
}
}
HeapPrint(&hp);
HeapDestroy(&hp);
}
检测
这里利用随机数来检测
void TestTopk()
{
int n = 100000;
int* a = (int*)malloc(sizeof(int)*n);
srand(time(0));
for (size_t i = 0; i < n; ++i)
{
a[i] = rand() % 1000000;
}
a[5] = 1000000 + 1;
a[1231] = 1000000 + 2;
a[531] = 1000000 + 3;
a[5121] = 1000000 + 4;
a[115] = 1000000 + 5;
a[2335] = 1000000 + 6;
a[9999] = 1000000 + 7;
a[76] = 1000000 + 8;
a[423] = 1000000 + 9;
a[3144] = 1000000 + 10;
PrintTopK(a, n, 10);
}
运行结果

代码总结
Heap.h 头文件
#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>
#include <string.h>
#include<time.h>
typedef int HPDataTpye;
typedef struct Heap
{
HPDataTpye* a;
int size;
int capacity;
}HP;
void Swap(int* px, int* py);
void AdjustDown(int* a, int n, int parent);
void AdjustUp(int* a, int child);
//void HeapInit(HP* php);
//初始化
void HeapInit(HP* php, HPDataTpye* a, int n);
// 插入x,保持他继续是堆
void HeapPush(HP* php, HPDataTpye x);
//判空
bool HeapEmpty(HP* php);
// 删除堆顶数据,删除后保持他继续是堆
void HeapPop(HP* php);
// 获取堆顶的数据,也就是最值
HPDataTpye HeapTop(HP* php);
//获取堆中元素个数
int HeapSize(HP* php);
//打印
void HeapPrint(HP* php);
//销毁堆
void HeapDestroy(HP* php);
Heap.c 函数文件
#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"
void Swap(int* px, int* py)
{
int tmp = *px;
*px = *py;
*py = tmp;
}
// 条件:左右子树都是小堆/大堆
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
// 选出左右孩子中小 or 大的那个
if (child + 1 < n && a[child + 1] < a[child])
{
++child;
}
// 1、如果小 or 大的孩子比父亲小 or 大,则交换,继续往下调整
// 2、如果小 or 大 的孩子比父亲大 or 小,则结束调整
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void AdjustUp(int* a, int child)
{
int parent = (child - 1) / 2;
//while (parent >= 0) 不对的 parent不会小于0
while (child > 0)
{
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void HeapInit(HP* php, HPDataTpye* a, int n)
{
assert(php);
//开辟空间
php->a = (HPDataTpye*)malloc(sizeof(HPDataTpye)*n);
if (php数据结构之堆