重温基础算法内部排序之堆排序法
Posted 顧棟
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了重温基础算法内部排序之堆排序法相关的知识,希望对你有一定的参考价值。
内部排序之堆排序法
文章目录
堆排序就是利用堆(Heap)这种数据结构进行排序,在堆排序算法中,我们使用的是最大堆(大根堆),堆排序是一种选择排序。
二叉堆定义
堆也是指二叉堆,是完全二叉树或者近似完全二叉树。
最大堆:当父结点的键值总是大于或等于任何一个子节点的键值。
最小堆:当父结点的键值总是小于或等于任何一个子节点的键值。
二叉堆的特性
- 父结点的键值总是大于(小于或等于)任何一个子结点的键值。
- 每个结点的左子树和右子树都是一个二叉堆(最大堆或最小堆)。
结点拥有的子树的个数称为结点的度(Degree)。
二叉树的特性
- 在二叉树的第 i \\mathrm i i 层上最多有 2 i − 1 \\mathrm 2^i-1 2i−1个结点( i ≥ 1 \\mathrmi\\geq1 i≥1)。
- 深度为 k \\mathrm k k 的二叉树至多有 2 k − 1 \\mathrm2^k-1 2k−1个结点( k ≥ 1 \\mathrmk\\geq1 k≥1)。
- 对任何一颗二叉树 T T T,如果其叶子结点个数为 n 0 \\mathrmn_0 n0,度为2的结点个数为 n 2 \\mathrmn_2 n2,则 n 0 = n 2 + 1 \\mathrmn_0=n_2+1 n0=n2+1。
完全二叉树的特性
- 具有 n \\mathrm n n个节点的完全二叉树的深度为 ⌊ l o g 2 n ⌋ + 1 \\mathrm\\left \\lfloor log_2^n\\right \\rfloor+1 ⌊log2n⌋+1,按层序编号,编号为i的结点的层次在 ∣ l o g 2 i ∣ + 1 \\mathrm\\left| log_2^i \\right|+1 ∣ ∣log2i∣ ∣+1
- 一棵深度为 k \\mathrm k k 的完全二叉树至少有 2 k − 1 \\mathrm2^k-1 2k−1的节点,至多 2 k − 1 \\mathrm2^k-1 2k−1个结点。
逻辑结构
完全二叉树的逻辑结构
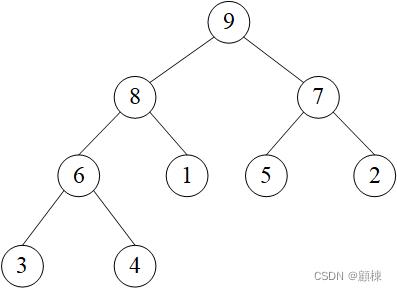
存储结构
使用数组来存储元素值。

数组的heapify
下标 0 0 0代表二叉树的根结点,将树按层从上至下,在同一层按从左往右,依次将结点的值存到数组中。如下图:
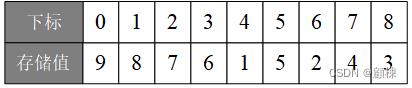
若数组下标为 i \\Large i i,则其左子树的下标为 2 ∗ i + 1 \\Large 2*i+1 2∗i+1,右子树的下标为 2 ∗ i + 2 \\Large 2*i+2 2∗i+2。其父结点的下标为 i − 1 2 ( i > 0 ) \\Large\\fraci-12 \\normalsize (i>0) 2i−1(i>0)。
主体思路:
- 寻找最后一个非叶子结点的下标。
- 从第一个非叶子结点的下标开始递减遍历数组。
- 设遍历下标变量用 i \\Large i i,在遍历过程中,比较其、其左子树的下标为 2 ∗ i + 1 \\Large 2*i+1 2∗i+1、右子树的下标为 2 ∗ i + 2 \\Large 2*i+2 2∗i+2的大小,将最大值放在 i \\Large i i的位置上。直到 i \\Large i i到0,数组heapify完成。
寻找最后一个非叶子结点
- 一个完全二叉树是完全填满的情况下,每一层的结点数是上一层的两倍,根结点的个数是1,最后一层的第一个结点(第一个叶子结点)的索引下标就是结点总数/2。那么最后一个非叶子节点的索引下标就是结点总数/2-1。
- 由于完全二叉树是依次填充,那么,最多存在一个度为1的结点(此结点只拥有一个左子结点),其他结点要么是度为2的结点,要么是度为0的结点。在完全二叉树不完全填满的情况下,总的结点数=度为2的结点个数+度为0的结点个数+1(可以理解度为1的结点个数)。结合上述二叉树的特性三(对任何一颗二叉树 T T T,如果其叶子结点个数为 n 0 \\mathrmn_0 n0,度为2的结点个数为 n 2 \\mathrmn_2 n2,则 n 0 = n 2 + 1 \\mathrmn_0=n_2+1 n0=n2+1。),第一个叶子节点的索引下标也为结点总数/2。那么最后一个非叶子节点的索引下标就是结点总数/2-1。
主要思想
- 将初始数组进行
heapify,满足二叉堆的特性。(按最大堆处理) - 目前下标 0 0 0的存储值是数组中最大的值,将下标 0 0 0和下标 8 8 8(数组 l e n g t h − 1 length-1 length−1)进行交换,此时下标 8 8 8就是最大值。
- 在下标
8
8
8不参与的情况下,再进行数组的
heapify,使得下标 0 0 0存储着剩余数组元素中的最大值,将下标 0 0 0与下标 7 7 7的值进行交换。此时下标 7 7 7,下标 8 8 8已经是经过排序的了。 - 重复以上步骤,将未排序的数组元素继续
heapify和首尾值交换。直到数组完全排序。
过程演示
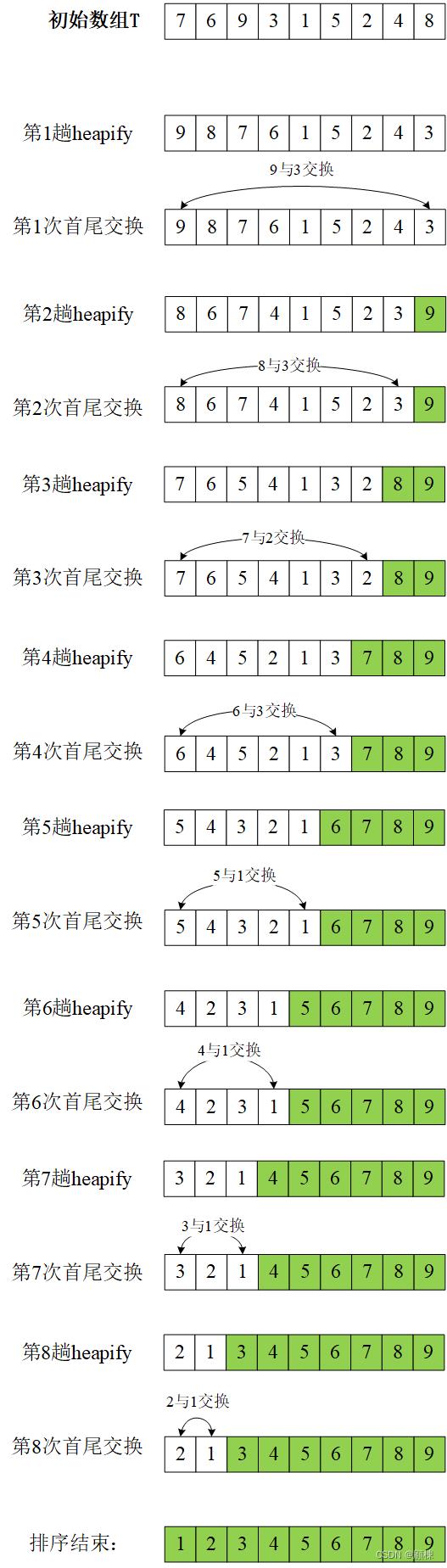
JAVA代码
package sort;
public class HeapSort
/**
* 将数组进行heapify
*/
private static void buildHeap(int[] o, int i, int length)
int leftChild = 2 * i + 1;
int rightChild = leftChild + 1;
int larger = i;
if (leftChild < length && o[leftChild] > o[larger])
larger = leftChild;
if (rightChild < length && o[rightChild] > o[larger])
larger = rightChild;
if (larger != i)
int temp = o[i];
o[i] = o[larger];
o[larger] = temp;
buildHeap(o, larger, length);
public static void main(String[] args)
int[] o = 7, 6, 9, 3, 1, 5, 2, 4, 8;
int count = 1;
System.out.print("heapify前: ");
for (int t : o)
System.out.print(t);
System.out.print(" ");
System.out.println();
// 算法部分
// init heapify
int i = o.length / 2 - 1;
for (; i >= 0; i--)
buildHeap(o, i, o.length);
System.out.print("第" + count + "趟heapify后: ");
for (int t : o)
System.out.print(t);
System.out.print(" ");
System.out.println();
// sort
for (int j = o.length - 1; j > 0; j--)
int temp = o[j];
o[j] = o[0];
o[0] = temp;
if (j == 1)
break;
buildHeap(o, 0, j);
count++;
System.out.print("第" + count + "趟heapify后: ");
for (int t : o)
System.out.print(t);
System.out.print(" ");
System.out.println();
System.out.print("排序后: ");
for (int t : o)
System.out.print(t);
System.out.print(" ");
System.out.println();
结果
heapify前: 7 6 9 3 1 5 2 4 8
第1趟heapify后: 9 8 7 6 1 5 2 4 3
第2趟heapify后: 8 6 7 4 1 5 2 3 9
第3趟heapify后: 7 6 5 4 1 3 2 8 9
第4趟heapify后: 6 4 5 2 1 3 7 8 9
第5趟heapify后: 5 4 3 2 1 6 7 8 9
第6趟heapify后: 4 2 3 1 5 6 7 8 9
第7趟heapify后: 3 2 1 4 5 6 7 8 9
第8趟heapify后: 2 1 3 4 5 6 7 8 9
排序后: 1 2 3 4 5 6 7 8 9
算法分析
整个堆排序的算法包含了初始化堆和重建堆两部分。
初始化堆的时间复杂度
在数组的初始堆化中,是从倒数第二层中的最后一个非叶子结点开始的。一个深度为 k k k的二叉堆,堆化过程中关键字比较次数一共最多 2 ( k − 1 ) 2(k-1) 2(k−1)。
那么深度为
h
h
h, 元素个数为n的二叉堆,
i
i
i代表堆的第几层,那么
i
i
i的取值就是从
h
−
1
∼
1
h-1 \\thicksim 1
h−1∼1。第i层上至多有
2
i
−
1
2^i-1
2i−1个结点,若以
i
i
i为根,那深度为
h
以上是关于重温基础算法内部排序之堆排序法的主要内容,如果未能解决你的问题,请参考以下文章