321. 拼接最大数

Posted 2021-09-22 炫云云

402. 移掉 K 位数字（中等)

316. 去除重复字母

321. 拼接最大数

321. 拼接最大数

题目描述

给定长度分别为  m  和  n  的两个数组，其元素由  0-9  构成，表示两个自然数各位上的数字。
现在从这两个数组中选出 k (k <= m + n)  个数字拼接成一个新的数，要求从同一个数组中取出的数字保持其在原数组中的相对顺序。

求满足该条件的最大数。结果返回一个表示该最大数的长度为  k  的数组。

说明: 请尽可能地优化你算法的时间和空间复杂度。

示例  1:

输入:
nums1 = [3, 4, 6, 5]
nums2 = [9, 1, 2, 5, 8, 3]
k = 5
输出:
[9, 8, 6, 5, 3]

示例 2:

输入:
nums1 = [6, 7]
nums2 = [6, 0, 4]
k = 5
输出:
[6, 7, 6, 0, 4]

示例 3:

输入:
nums1 = [3, 9]
nums2 = [8, 9]
k = 3
输出:
[9, 8, 9]

思路

和第一道题类似，只不不过这一次是两个数组，而不是一个，并且是求最大数。

最大最小是无关紧要的，关键在于是两个数组，并且要求从两个数组选取的元素个数加起来一共是 $k$。

然而在一个数组中取 $k$ 个数字，并保持其最小（或者最大），我们已经会了。但是如果问题扩展到两个，会有什么变化呢？

实际上，问题本质并没有发生变化。 假设我们从 nums1 中取了 k1 个，从 num2 中取了 k2 个，其中 k1 + k2 = k。而 k1 和 k2 这 两个子问题我们是会解决的。由于这两个子问题是相互独立的，因此我们只需要分别求解，然后将结果合并即可。

假如 k1 和 k2 个数字，已经取出来了。那么剩下要做的就是将这个长度分别为 k1 和 k2 的数字，合并成一个长度为 k 的数组合并成一个最大的数组。

以题目的 nums1 = [3, 4, 6, 5] nums2 = [9, 1, 2, 5, 8, 3] k = 5 为例。 假如我们从 num1 中取出 1 个数字，那么就要从 nums2 中取出 4 个数字。

运用第一题的方法，我们计算出应该取 nums1 的 [6]，并取 nums2 的 [9,5,8,3]。 如何将 [6] 和 [9,5,8,3]，使得数字尽可能大，并且保持相对位置不变呢？

实际上这个过程有点类似归并排序中的治，而上面我们分别计算 num1 和 num2 的最大数的过程类似归并排序中的分治。

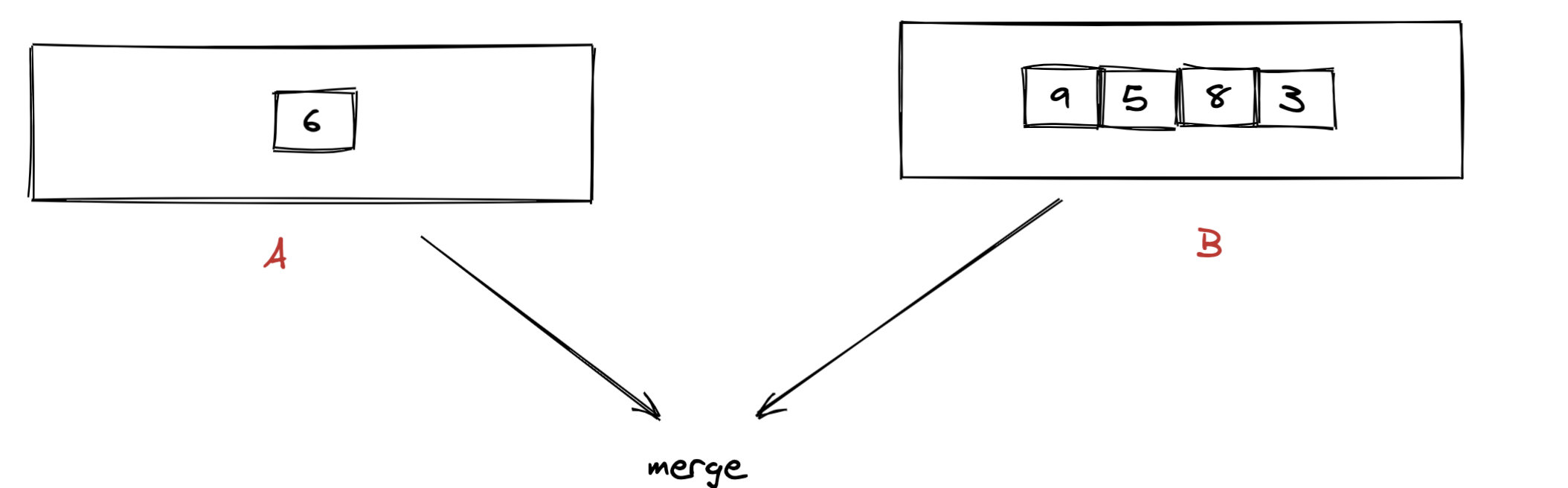
代码：

我们将从 num1 中挑选的 k1 个数组成的数组称之为 A，将从 num2 中挑选的 k2 个数组成的数组称之为 $B$，

def merge(A, B):
    ans = []
    while A or B:
        bigger = A if A > B else B
        ans.append(bigger[0])
        bigger.pop(0)
    return ans

这里需要说明一下。 在很多编程语言中：如果 A 和 B 是两个数组，当前仅当 A 的首个元素字典序大于 B 的首个元素，A > B 返回 true，否则返回 false。

比如：

A = [1,2]
B = [2]
A < B # True

A = [1,2]
B = [1,2,3]
A < B # False

以合并 [6] 和 [9,5,8,3] 为例，图解过程如下：

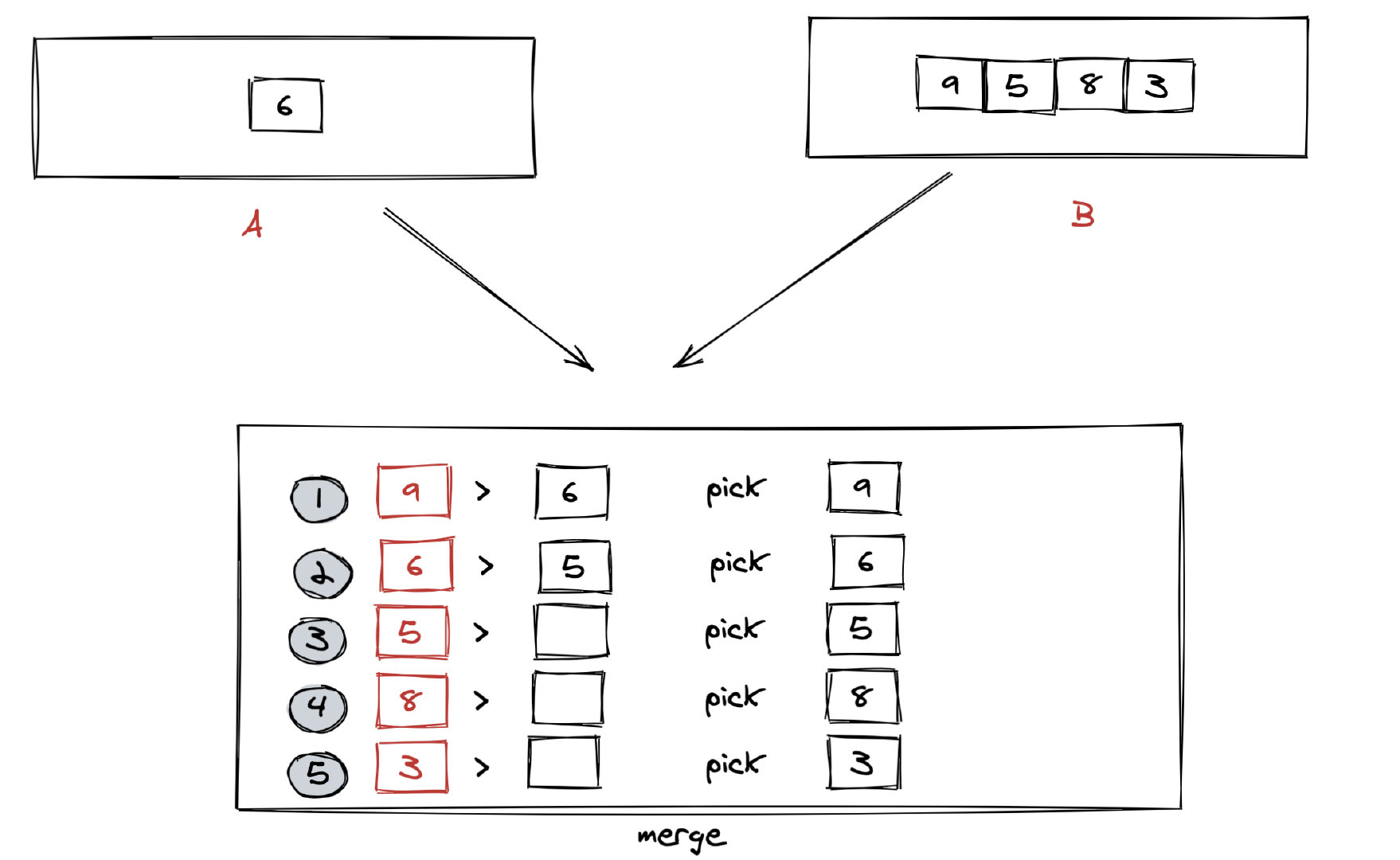
具体算法：

• 从 nums1 中 取 $min(i,len(nums1))$ 个数形成新的数组 A（取的逻辑同第一题），其中 i 等于 0,1,2, … k。
• 从 nums2 中 对应取 $min(j,len(nums2))$ 个数形成新的数组 B（取的逻辑同第一题），其中 j 等于 k - i。
• 将 A 和 B 按照上面的 merge 方法合并
• 上面我们暴力了 k 种组合情况，我们只需要将 k 种情况取出最大值即可。

class Solution:
    def maxNumber(self, nums1, nums2, k):
        def pick_max(nums, k):# 保留 nums里k个最大数
            stack = []
            drop = len(nums) - k
            for num in nums:
                while drop and stack and stack[-1] <num: # 当前数据左边比右边小，丢弃左边，直到drop=0
                    stack.pop()
                    drop -=1
                stack.append(num)
            return stack[:k]

        def merge(A,B):
            ans = []
            while A or B:
                bigger = A if A>B else B
                ans.append(bigger[0])
                bigger.pop(0)
            return ans
        res = []
        for i in range(k+1):
            if i <= len(nums1) and k-i <=len(nums2):
                ans = merge(pick_max(nums1,i) , pick_max(nums2,k-i))
                if res<ans:
                    res = ans
        return res


            

复杂度分析

• 时间复杂度：pick_max 的时间复杂度为 $O(M+N)$ ，其中 $M$ 为 nums1 的长度，$N$ 为 nums2 的长度。 merge 的时间复杂度为 $O(k)$，再加上外层遍历所有的 k 中可能性。因此总的时间复杂度为 $O(k^2\ast (M+N))$。
• 空间复杂度：我们使用了额外的 stack 和 ans 数组，因此空间复杂度为 $O(max(M,N,k))$，其中 $M$ 为 nums1 的长度，$N$ 为 nums2 的长度。

总结

这三道题都是删除或者保留若干个字符，使得剩下的数字最小（或最大）或者字典序最小（或最大）。我们贪心地删除栈中相邻的字符。如果你会了这个套路，那么这四个题目应该都可以轻松解决。

316. 去除重复字母（困难），我们使用 hashmap 代替了数组的遍历查找，属于典型的空间换时间方式，可以认识到数据结构的灵活使用是多么的重要。背后的思路是怎么样的？为什么想到空间换时间的方式，我在文中也进行了详细的说明，这都是值得大家思考的问题。然而实际上，这些题目中使用的栈也都是空间换时间的思想。大家下次碰到需要空间换取时间的场景，是否能够想到本文给大家介绍的栈和哈希表呢？

321. 拼接最大数（困难）则需要我们能够对问题进行分解，这绝对不是一件简单的事情。但是对难以解决的问题进行分解是一种很重要的技能，希望大家能够通过这道题加深这种分治思想的理解。 大家可以结合我之前写过的几个题解练习一下，它们分别是：

• 剑指 Offer 51. 数组中的逆序对
• 53. 最大子序和