数据结构树与二叉树

Posted 2021-09-20 盖丽男

定义

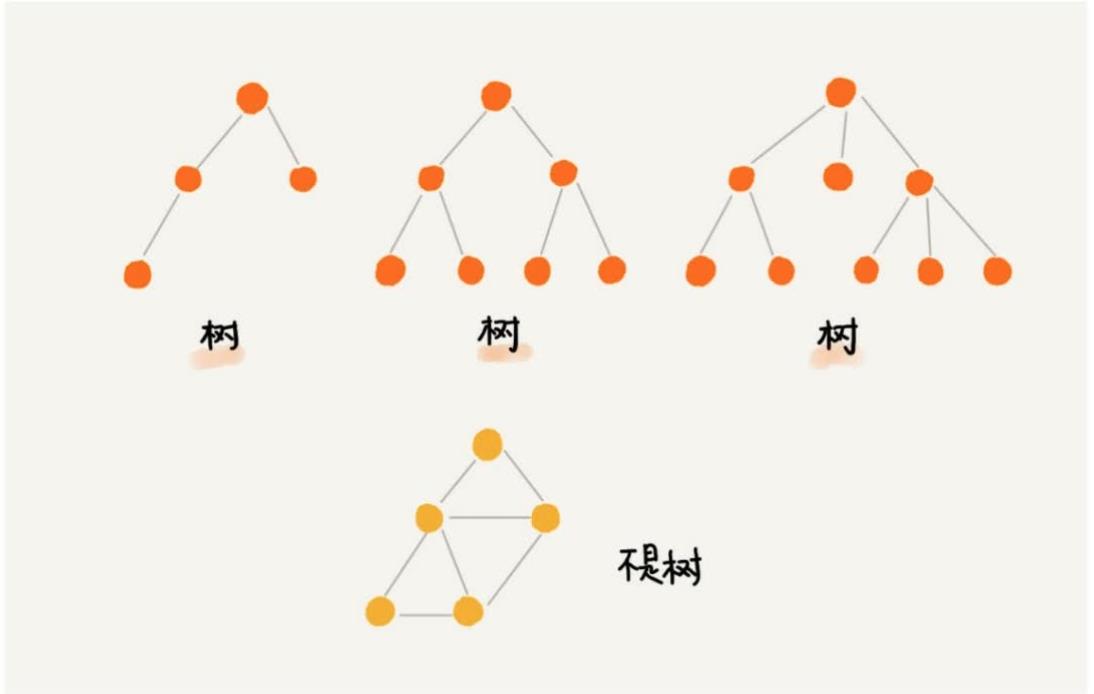
树（Tree）是n（n>=0）个结点的有限集。n=0时称为空树。在任意一颗非空树中：

有且仅有一个特定的称为根（root）的结点；
当n>1时，其余结点可分为m(m>0)个互补交互的有限集T1、T2…Tm，其中每一个集合本身又是一棵树，并称为根的子树（SubTree）。

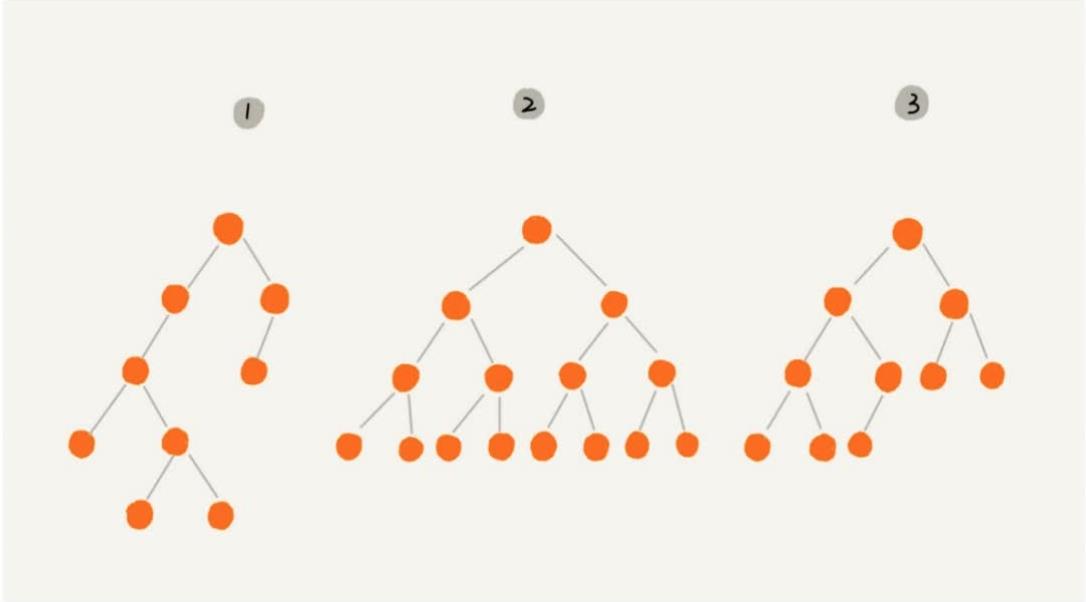
二叉树是另一种树形结构，其特点是每个结点至多只有两颗子树（即二叉树中不存在度大于2的结点），并且，二叉树的子树有左右之分，其次序不能任意颠倒。
与树相似，二叉树也以递归的形式定义。二叉树是n(n≥0)个结点的有限集合：
①或者为空二叉树，及n=0。
②或者由一个根结点和两个互不相交的称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。
二叉树有五种不同的基本形态： A：空二又树 B：只有一个根结点的二叉树 C：右子树为空的二叉树 D：左子树为空的二叉树 E：左、右子树都非空的二叉树

结构

数组和链表都可以用来表示二叉树，当然如果你想，字符串也可以用来表示树。
我们还可以自己定义二叉树的数据结构，比如

@Data
public class Tree {
    private Tree left;
    private Tree right;
    private String value;
}

应用

二叉搜索树

二叉搜索树是一种节点值之间具有一定数量级次序的二叉树，对于树中每个节点：

若其左子树存在，则其左子树中每个节点的值都不大于该节点值；
若其右子树存在，则其右子树中每个节点的值都不小于该节点值。

红黑树

R-B Tree，全称是Red-Black Tree，又称为“红黑树”，它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色，可以是红(Red)或黑(Black)。

红黑树的特性:
（1）每个节点或者是黑色，或者是红色。
（2）根节点是黑色。
（3）每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！]
（4）如果一个节点是红色的，则它的子节点必须是黑色的。
（5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

遍历

二叉树的遍历

void traverse(TreeNode root) {
    // 前序遍历代码位置
    traverse(root.left)
    // 中序遍历代码位置
    traverse(root.right)
    // 后序遍历代码位置
}

引用

二叉树的基本概念
【数据结构】树的定义和树的三种存储结构