王道数据结构5（树与二叉树）

Posted 晨沉宸辰

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了王道数据结构5（树与二叉树）相关的知识，希望对你有一定的参考价值。

树与二叉树

一、树的基本概念

树型结构属于非线性结构（元素的前驱和后继的个数不是为1的），这一节讲的树形结构元素的前驱个数为1，但是元素的后继个数不是为1了（可以有多个后继），所以说树形机构元素的关系是一对多或者多对多的。树型结构的特点是节点之间是有分支的，并且还具有层次关系。

（一）树的基本概念

  1. 树(Tree)是n(n≥0)个结点的有限集合T，若n=0时称为空树，否则:
    (1)有且只有一个特殊的称为树的根(Root)结点;
    (2)若n>1时， 其余的结点被分为m(m>0)个互不相交的子集 T T T1 , T ,T ,T2, T T T3 … T T Tm ,其中每个子集本身又是一棵树，称其为根的子树(Subtree)。
  2. 这是树的递归定义，即用树来定义树，树是一种递归的数据结构。树作为一种逻辑结构，同时也是一种分层结构，具有以下两个特点：
    （1）树的根节点没有前驱，除根节点外的所有结点有且仅有一个前驱
    （2）树种所有结点可以有零个或多个后继
  3. 树适合于表示具有层次结构的数据，树中的某个节点（除根节点外）最多只和上一层的一个结点（其父节点）有直接关系，根节点没有直接上层结点，因此在n个结点的树种有n-1条边，而树中每个结点与其下一层的零个或多个节点（及其子女结点）有直接关系

（二）树的基本术语

（A）结点相关

  1. 结点
  2. 结点的度
  3. 树的度：树中结点度最大值
  4. 叶子结点（终端结点）、非叶子结点（非终端结点或分支结点）：除根结点以外，分支结点又称为内部结点。
  5. 孩子结点、双亲结点、兄弟结点：一个结点的子树的根称为该结点的孩子结点，该结点是孩子结点的双亲结点或父结点，同一双亲结点的所有子结点互称为兄弟结点
  6. 层次：规定树中根结点的层次为1，其余结点的层次等于其双亲结点的层次加1
  7. 层次路径：从根结点开始，到达某结点p所经过的所有结点成为结点p的层次路径（有且仅有一条）【同一双亲的两个孩子之间不存在路径】
  8. 堂兄结点：双亲结点在同一层上的所有结点互称为堂兄结点
  9. 祖先结点：结点p的层次路径上的所有结点（p除外）称为p的祖先
  10. 子孙结点：子树中的任意结点

（B）树整体相关

  1. 树的深度：树中结点的最大层次值，又称为树的高度
  2. 有序树和无序树：对于一棵树，若其中每一个结点的子树(若有）具有一定的次序，则称为有序树
  3. 森林：是m（m≥0）棵互不相交的树的集合。显然，若将一棵树的根结点删除，剩余的子树就构成了森林。【m=0，表示空森林】
  4. 结点的高度：从叶结点开始从底向上逐层累加
  5. 结点的深度：从根结点开始从顶向下逐层累加

（三）树的表示形式

（1）倒悬树：最常用的表示形式
（2）嵌套集合：是一些集合的集体，对于任何两个集合，或者不想交，或者一个集合包含另一个集合
（3）广义表形式：例如（A(B(E(K,L),F),C(G(M,N),D(H,I,J)
（4）凹入法表示形式

（四）树的性质

  1. 结点数=总度数+1
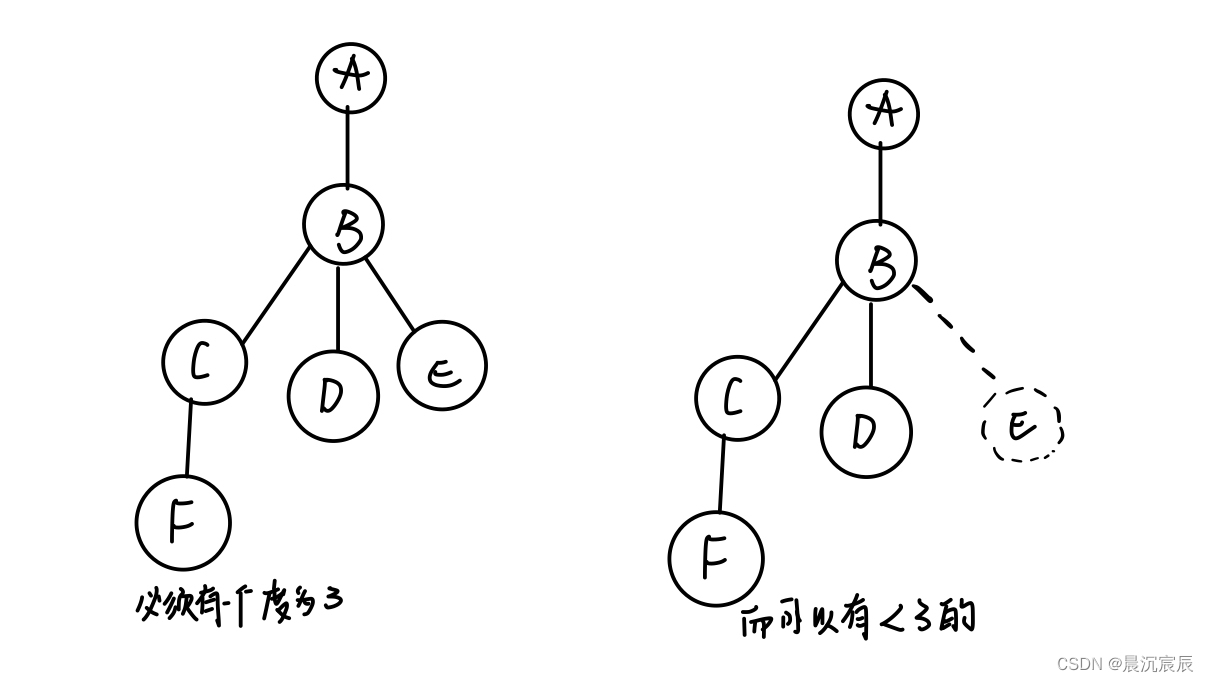
  2. 区分度为m的树，m叉树
    度为m的树：各结点的度最大值为m，但是其他结点的度不一定是m
    m叉树：每个结点最多只能有m个孩子的树
度为m的树m叉树
任意结点的度≤m（最多m个孩子）任意结点的度≤m（最多m个孩子）
至少有一个结点度=m允许所有结点的度都<m
一定是非空树，至少有一个m+1个结点可以是空树


3. 度为m的树第i层至多有mi-1 个结点（i≥1）
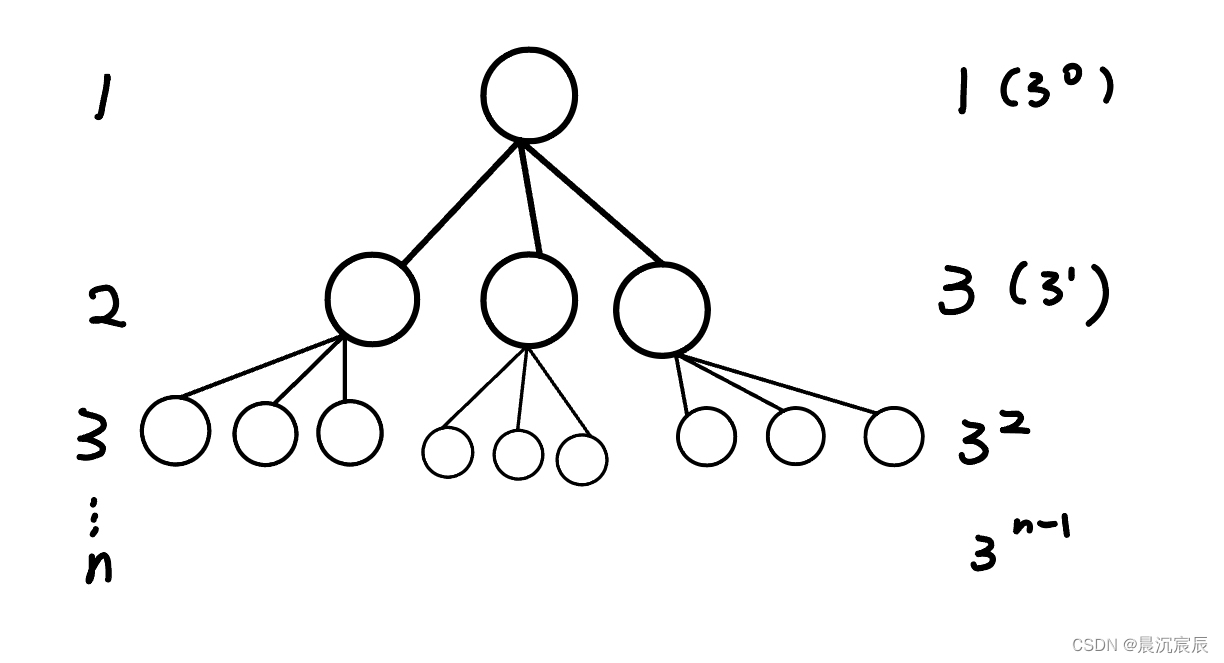4. m叉树第i层至多有mi-1个结点（i≥1）
4. 高度为h的m叉树至多有 (mh-1) /(m-1)个结点:m0+m1…+mn
5. 高度为h的m叉树至少有h个结点
6. 高度为h，度为m的树至少有h+m-1个结点
7. 具有h个结点的m叉树的最小高度为[logm(n(m-1)+1)]

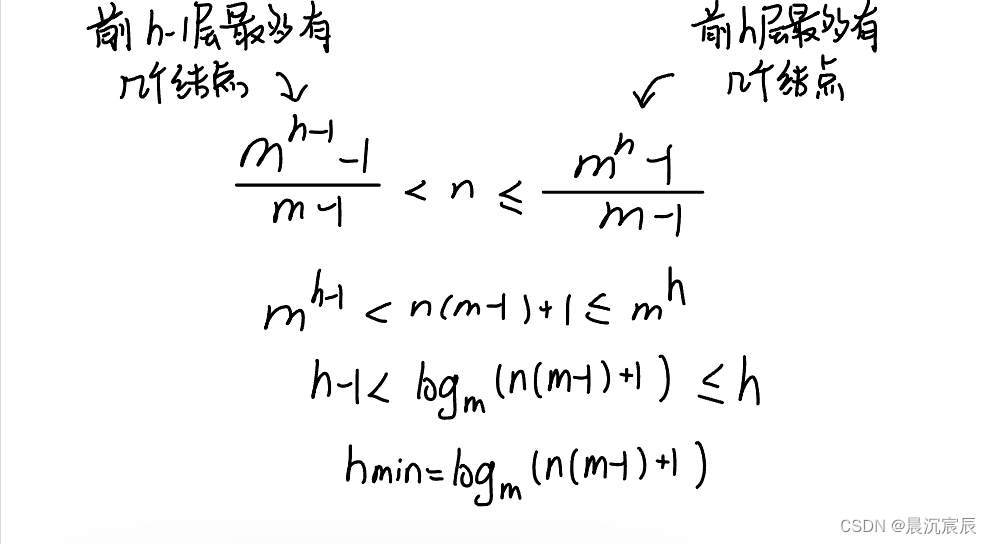
二、二叉树

（一）二叉树的定义

  1. 特点：①每个结点至多只有两棵子树 ②左右子树不能颠倒（二叉树是有序树）
  2. 二叉树(Binary tree )是n(n≥0)个结点的有限集合。
    若n=0时称为空树,否则:
    (1)有且只有一个特殊的称为树的根(Root)结点;
    (2)若n>1时，其余的结点被分成为二个互不相交的子集 T T T1 , T T T2 ,分别称之为左、右子树，并且左、右子树又都是二叉树。
    由此可知，二叉树的定义是递归的。
  3. 特点：二叉树结构简单，存储效率高，树的操作算法相对简单，且任何树都很容易转化成二叉树
  4. 二叉树的形态：（1）空二叉树（2）单结点二叉树（3）右子树为空（4）左子树为空（5）左右子树都不为空
  5. 二叉树与度为2的树的区别：
  • 度为2的树至少有3个结点，而二叉树可以为空
  • 度为2的有序树的孩子的左右次序是相对另一孩子而言的，若某个结点只有一个孩子，则这个孩子就无须区分其左右次序，而二叉树无论其孩子数是否为2，均需确定其左右次序，次序就是确定的

（二）几个特殊的二叉树

1. 满二叉树

（1）一棵高度为h，且含有2h - 1个结点的二叉树
（2）特点：
①只有最后一层有叶子结点
②不存在度为 1 的结点
③按层序从 1 开始编号，结点 i 的左孩子为 2i，右孩子为 2i+1；结点 i 的父节点为 i/2 （如果有的话）
（3）基本特点：a.是每一层上的结点数总是最大结点数。b. 满二叉树的所有的支结点都有左、右子树。c. 可对满二叉树的结点进行连续编号，若规定从根结点开始，按“自上而下、自左至右”的原则进行。

2. 完全二叉树

（1）当且仅当其每个结点都与高度为h的满二叉树中编号为1～n的结点一一对应时，称为完全二叉树
（2） 特点：
①只有最后两层可能有叶子结点
②最多只有一个度为1的结点
③同左③ ④ i≤ n/2 为分支结点， i> n/2 为叶子结点

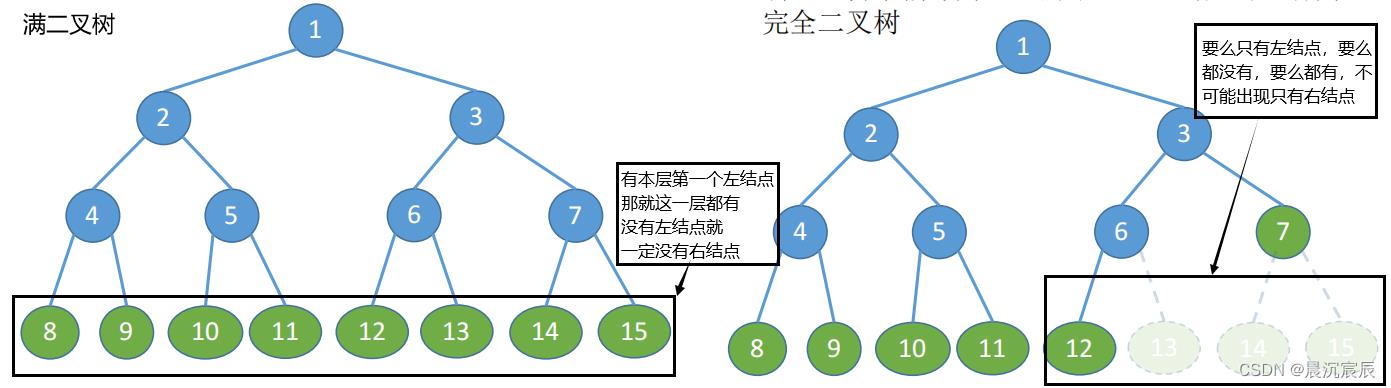
（3）完全二叉树是满二叉树的一部分，而满二叉树是完全二叉树的特例
（4）特点：① 若完全二叉树的深度为 k k k ，则所有的叶子结点都出现在第 K K K 层或 K − 1 K-1 K−1 层 ② 对于任意结点，如果其右子树的最大层次为 l l l ，则左子树的最大层次为 l l l 或 l + 1 l+1 l+1
（5）性质：
① n个结点的完全二叉树深度为 [ l o g   2   n ] + 1 [log~2~n]+1 [log 2 n]+1
②若对一棵有n个结点的完全二叉树(深度为 [ l o g   2   n ] + 1 [log~2~n]+1 [log 2 n]+1 的结点按层(从第1层到第 [ l o g   2   n ] + 1 [log~2~n]+1 [log 2 n]+1 层)序自左至右进行编号，则对于编号为 i i i ( 1 ≤ i ≤ n 1≤i≤n 1≤i≤n)的结点:
a. 若i=1:则结点i是二叉树的根，无双亲结点;否则，若i>1,则其双亲结点编号是[i/2]。
b. 如果2i>n:则结点i为叶子结点，无左孩子;否则，其左孩子结点编号是2i。
c. 如果2i+1>n:则结点i无右孩子;否则，其右孩子结点编号是2i+1。

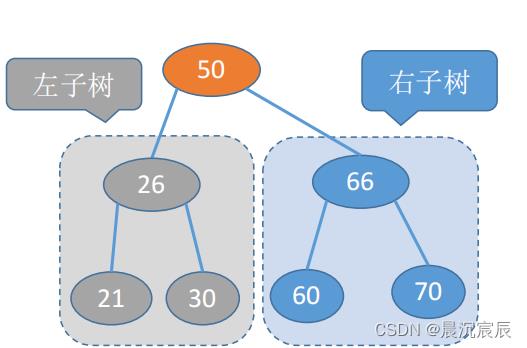
3. 二叉排序树

  1. 一棵二叉树或者是空二叉树，或者是具有如下性质的二叉树：
    （1）左子树上所有结点的关键字均小于根结点的关键字；
    （2）右子树上所有结点的关键字均大于根结点的关键字。
    左子树和右子树又各是一棵二叉排序树。
  2. 左子树关键字<根节点关键字<右子树关键字

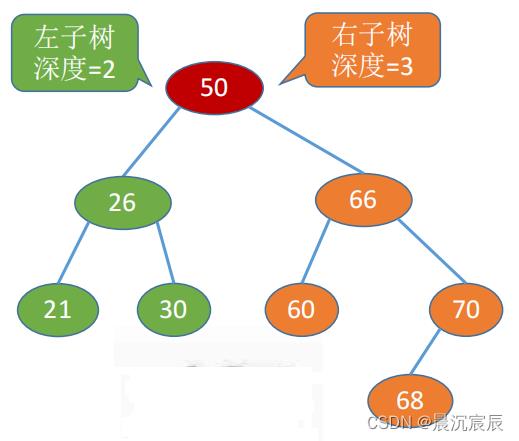
4. 平衡二叉树

  1. 树上任一结点的左子树和右子树的深度之差不超过1。
  2. 平衡的二叉树可以有更高的搜索效率

(三) 二叉树的性质

1. 基础性质

1.设非空二叉树中度为0、1和2的结点个数分别为n0、n1和n2，则 n0 = n2 + 1（叶子结点比二分支结点多一个）
假设树中结点总数为 n，则
① n = n0 + n1 + n2 ② n = n1 + 2n2 +1 => ② - ①n0 = n2 + 1
2. 二叉树第 i 层至多有 2i-1 个结点（i≥1） m叉树第 i 层至多有 mi-1 个结点（i≥1）
3. 高度为h的二叉树至多有 2^ℎ − 1个结点（满二叉树),高度为h的m叉树至多有(mh^-1) /(m-1)个结点

2. 完全二叉树性质

  1. 具有n个（n > 0）结点的完全二叉树的高度h为 [log2(n+1)]或[log2n]+1
  2. 对于完全二叉树，可以由的结点数 n 推出度为0、1和2的结点个数为n0、n1和n2，完全二叉树最多只有一个度为1的结点，即n1=0或1 n0 = n2 + 1 则 n0 + n2 一定是奇数
    ①若完全二叉树有2k个（偶数）个结点，则必有n1=1， n0 = k，n2 = k-1
    ② 若完全二叉树有2k-1个(奇数)个结点，则必有n1=0，n0 = k，n2 = k-1

(四）二叉树的顺序存储

  1. 基础实现：
#define MaxSize 100
struct TreNode
   ElemType value; //结点中的数据元素
   bool isEmpty;//结点是否为空

;
TreeNode t[MaxSize];

定义一个长度为MaxSize的数组t，按照从上至下，从左至右的顺序依次存储完全二叉树中的各个结点。

^123456789101112^^^^
  1. 初始化
bool InitT(TreeNode L[])
   for(int i=0;i<MaxSize;i++)
    t[i].isEmpty=true;
  1. 完全二叉树查找是否有左右孩子双亲，可以用：设当前结点为i
  • 如果2i≤n，那么就存在左孩子
  • 如果2i+1≤n，那么就存在右孩子
  • 如果i＞[n/2]，那么就是叶子结点，反之，是分支结点
  1. 如果不是完全二叉树是不可以用上述结论。需要重新设计
  2. 如果是一个普通二叉树，需要编号与完全二叉树一一对应起来，如下
^123^567^^^1112^^^^

这样就形成二叉树如图

6. 对于顺序存储而言，最坏的情况下，一个深度为k且只有k个结点的单支树需要长度为2k-1的一位数组

(五）二叉树的链式存储

  1. 实现方式;
typedef struct BiTNood
   ElemType value; //结点中的数据元素
  struct BiTNode *lchild,*rchild;
BiTNode,*BiTree;

注意：n个结点的二叉链表共有n+1个空链域，因此可以用于构造线索二叉树

struct ElemType
  int value;
;
typedef struct BiTNood
   ElemType value; //结点中的数据元素
  struct BiTNode *lchild,*rchild;
BiTNode,*BiTree;
//定义一个空树
BiTree root=NULL;
//插入根节点
root = (BiTree)malloc(sizeof(BiTNode));
root->data=1;
root->lchild=NULL;
root->rchild=Null;
//插入新结点
BiTNode *p=(BiTNode *)malloc(sizeif(BiTNode));
p->data=2;
p->lchild=NULL;
p->rchild=NULL;
root->lchild=p;

问题是：很难找到父节点（寻找子结点简单）

  1. 加入双亲结点的存储（三叉链表）
typedef struct BiTNood
   ElemType value; //结点中的数据元素
  struct BiTNode *lchild,*rchild;
   struct BiTNode *parent;
BiTNode,*BiTree;

(六) 先中后序遍历 （递归算法）

先序：根左右（前缀表达式）
中序：左根右（中缀表达式）
后序：左右根（后缀表达式）

1. 先序遍历

（1）规则：想访问根节点后访问左结点，右结点
（2）代码思想：
① 如果二叉树为空，那就什么也不做
② 如果二叉树非空，先序遍历左子树，访问根节点，先序遍历右子树
（3）代码：

typedef struct BiTNood
   ElemType value; //结点中的数据元素
  struct BiTNode *lchild,*rchild;
BiTNode,*BiTree;
void InOrder(BiTree T)
  if(T!=NULL)
   visit(T);
    InOrder(T->lchild);
    InOrder(T->rchild);

（4）分析：①空间复杂度：O(h)
② 每一个结点都会在第一次访问时处理
③每一个结点都会路过三次

2. 中序遍历

（1）代码实现：

  if(T!=NULL)
    InOrder(T->lchild);
    visit(T);
    InOrder(T->rchild);

（2）分析：①只有在第二次路过结点时才会访问 ②空间复杂度 O（h）

3. 后序遍历

（1）代码实现：

  if(T!=NULL)
    InOrder(T->lchild);
    InOrder(T->rchild);
    visit(T);

（2）分析：①只有在第三次路过结点时才会访问 ②空间复杂度 O（h）

（七）先中后序遍历（非递归算法）

void preorder1(BiTree root)

    BiTree s[MAX_TREE_SIZE],p;
    int top;
    top=0;
    p=root;
    while(p||top>0)
    
        while(p)
        
            cout<<p->data<<" ";
            top++;
            s.[top]=p;
            p=p->lchild;   
        
        if(top>0)
        
            p=s[top];
            top--;
            p=p->rchild;

前中后都差不多，不过是顺序变化

（八）层次遍历

  1. 算法思想：
    （1）初始化一个辅助队列
    （2）跟结点入队
    （3）若队列非空，则队头结点出队，访问该结点，并将其左、右结点插入队尾
    （4）重复（3）直到队列为空
  2. 代码实现（顺序存储方式）：
//；二叉树的顺序储存结构
#define MAX_TREE 10000;
typedef  Telemtype SiTree[MAX_PATH];
SiTree bT;
void leveltree(BiTree *t)

      BiTree s[100],p;
      int front rear;
    front=rear=0;
    p=t;
     if(t!=NULL)
     
         rear++;
         s[rear]=p;
         while(front!=rear)
           front++;
            p=s[front];
            count<<p->data;
            if(p->lchild)
            
                rear++;
                s[rear]=p->lchild;
                
            
             if(p->rchild)
            
                rear++;
                s[rear]=p->rchild;
  1. 代码实现（链队列）
typedef struct Bnode	/*定义二叉树存储结构*/
 char data;
  struct Bnode *lchild,*rchild;
Bnode,*Btree;
 
void Createtree(Btree &T)	/*创建二叉树函数*/

    //按先序次序输入二叉树中结点的值（一个字符），创建二叉链表表示的二叉树T
	char ch;
	cin >> ch;
	if(ch=='#')
        T=NULL;			//递归结束，建空树
	else
		T=new Bnode;
		T->data=ch;					//生成根结点
		Createtree(T->lchild);	//递归创建左子树
		Createtree(T->rchild);	//递归创建右子树
	
    return;

bool Leveltraverse(Btree T)

    Btree p;
    if(!T)
        return false;
    queue<Btree>Q; //创建一个普通队列(先进先出)，里面存放指针类型
    Q.push(T); //根指针入队
    while(!Q.empty()) //如果队列不空
    
        p=Q.front();//取出队头元素
        Q.pop(); //队头元素出队
        cout<<p->data<<"\\t";
        if(p->lchild)
            Q.push(p->lchild); //左孩子指针入队
        if(p->rchild)
            Q.push(p->rchild); //右孩子指针入队
    
    return true;
 
int main()
  Btree mytree;
    Createtree(mytree);//创建二叉树
    Leveltraverse(mytree);//层次遍历二叉树
    return 0;

（九）构造二叉树

1. 根据遍历构造二叉树

  1. 分析可以发现，一个已知二叉树的先中后序遍历顺序一定，但是一个已知的先中后序遍历得到的树是不一定的
  2. 层次遍历也是不一定的
  3. 给出先中后序一种是无法得到确定的二叉树，因此需要进行组合（先+中）（中+后）（中+层次）注意：前+后是无法得到唯一的，一定要有中序序列，缺少中序无论如何组合都没有办法得到唯一的树。
  4. 以给出前序+中序构造二叉树为例，方法技巧：
    ① 前序第一个结点一定是根结点（层次遍历第一个也是根结点，后序遍历的最后一个结点一定是根结点），进而可以在中序中寻得被根结点分开的两部分
    ② 中序中前部分为左树，后部分为右树，可以利用这两部分的长度去分开前序中的左右子树。
    ③ 利用递归的思想，每一个子树都适用
  5. 总结：找到树的根结点，并根据中序序列划分左右子树，再找到左右子树根结点

2. 代码构造二叉树

void creatree(BiTree &t);

    char ch;
    count<<ch<<" ";
    t->data=ch;
    if(ch!='@')
    
        t=new BiTNode;
        creatree(t->lchild);
        creatree(t->rchild);
        
    
    else 
        t=NULL;

三、线索二叉树

  1. 二叉树存在的问题：
    （1）每次进行遍历的时候，只能从根结点开始遍历某个子树，无法从分支或叶子结点开始遍历整个树
    （2）无法找到一个结点的遍历顺序中的前驱，只能设置两个指针，一个记录，当前一个记录上一个被访问的结点，才有可能得到前驱，要经过一个完整的遍历
  2. 改进：利用n个结点的树有n+1个空链域，空链域指向前后驱，没有前驱后继设置为NULL，分为前驱线索（左孩子充当），后继线索（右孩子充当）。

（一）线索二叉树的存储结构

  1. 代码实现
typedef struct ThreadNode
  ElemType data;
  struct ThreadNode *lchild,*rchild;
  int ltag,rtag;
ThreadNode,*ThreadTree;
  1. 结构
*lchildltagdatartag*rchild

tag=0 的时候指向自己的左右孩子
tag=1 的时候指向的是自己的前后驱（说明没有孩子）
3. 画出线索二叉树

（二）对二叉树进行线索化

  1. 以中序为例
    附设一个指针pre始终指向刚访问的结点，若指针p指向当前访问的结点，则pre指向他的前驱。
    下面以中序线索树的建立为例，介绍在中序遍历过程中如何修改结点的左、右指针域，以保存当前访问结点的“前驱”和“后继”信息。附设指针pre, 并始终保持指针pre指向当前访问的由指针p所指结点的前驱。
typedef struct ThreadNode
  ElemType data;
  struct ThreadNode *lchild,*rchild;
  int ltag,rtag;
ThreadNode,*ThreadTree;
ThreadNode *pre = NULL;
//中序线索二叉树
void CreateInThread(ThreadTree T)
  pre = NULL; //pre初始为NULL
  if(T!=NULL)  //非空二叉树才可以进行线索化
     InThread(T);  //终须线索化二叉树
     if(pre->rchild==NULL)
               pre->rtag=1; //处理遍历的最后一结点
  

//中序遍历二叉树，一边遍历一边中序线索化
void InTread(ThreadTree T)
 if(T!=NULL)
    InThread(T->lchild);
    visit<
以上是关于王道数据结构5（树与二叉树）的主要内容，如果未能解决你的问题，请参考以下文章
 

 王道数据结构5（树与二叉树）


 树与二叉树


 树与二叉树


 树与二叉树


 数据结构-王道2017-第4章 树与二叉树-二叉树的遍历


 (王道408考研数据结构)第五章树-第三节4：树与二叉树的转换