初阶数据结构完全二叉树实现堆排序

Posted 2021-09-19 赏一杯茶：

堆排序算法

• • • 一、完全二叉树的介绍
    • 二、堆向下调整算法
    • 三、堆排序算法

前言

完全二叉树是效率很高的数据结构，用它进行排序算法时时间复杂度大大降低

一、完全二叉树的介绍

完全二叉树是由满二叉树引出来的。对于深度为K，有n个结点的二叉树，当且仅当其每一个节点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。满二叉树是一种特殊的完全二叉树。

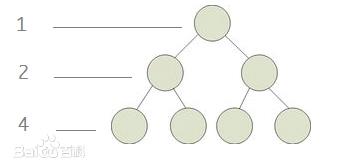
如上图示为满二叉树，深度K为3，结点n为7，即满二叉树的结点n与深度K存在关系为：n = 2^k - 1.

如上图示为完全二叉树，完全二叉树有如下性质：

1. K-1层全满，K层不满，即2^(K-1)<= n <= 2 ^(K) - 2;
2. 第K层结点从左至右连续，故度为1的结点（只有一个孩子的结点）不大于1个
3. n = n0(叶子结点) + n1(度为1的结点) + n2（度为2的结点），由于n1<=1，且n2 = n0 - 1

顺序存储二叉树：
顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树.
上图二叉树物理表示为{0,1,2,3,4},{0,1,2,3,4,5}

二、堆向下调整算法

认识堆向下调整算法之前先了解下“大堆”与“小堆”

下图为小堆示例图，即父节点总小于子节点

此为大堆结构示例图，即父节点总大于子节点

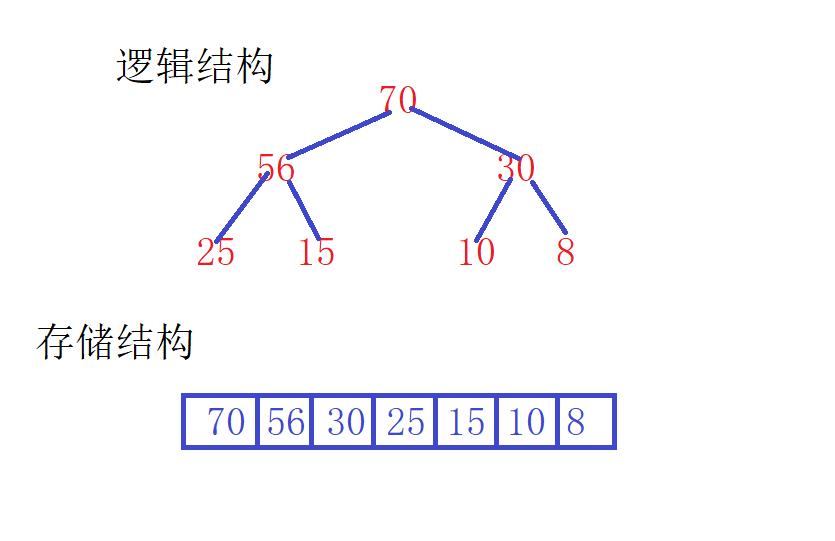
顾名思义，向下调整算法即父节点与子节点比较调整

通过一个完全二叉树{27,15,19,18,28,34,65,49,25,37}了解向下调整算法

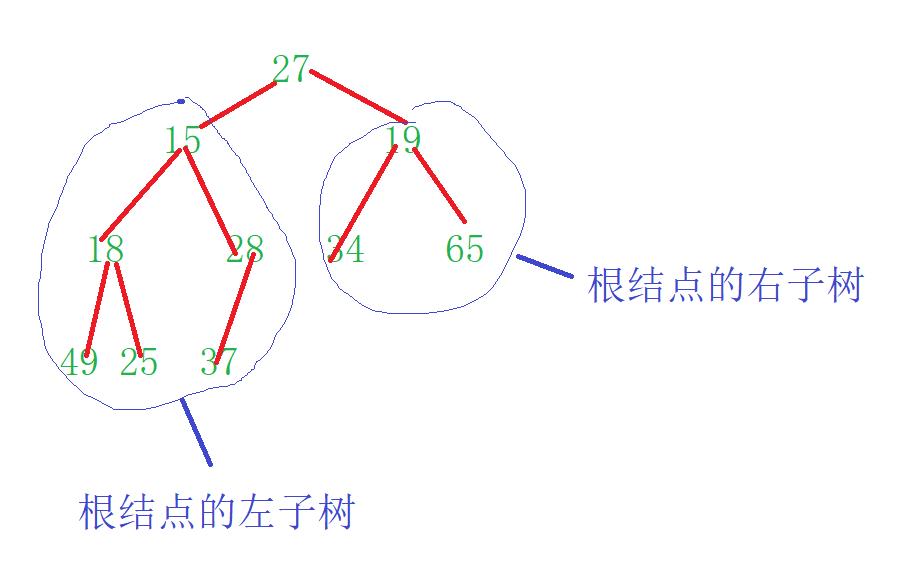
这是一个“伪小堆”，即除根结点外，根节点的左子树与右子树均满足小堆排序，将整体排为小堆后是{15,18,19,25,28,34,65,49,27,37}，下面给出图解：

最终变成：

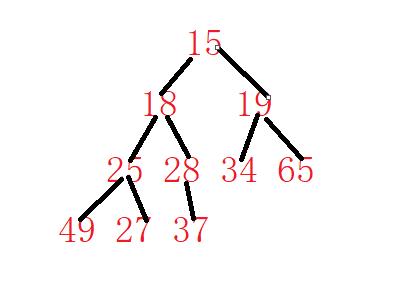
代码：

void Swap(int* a, int x, int y)
{
	int tmp = 0;
	tmp = a[x];
	a[x] = a[y];
	a[y] = tmp;
}
void Adjustdown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1< n && a[child] > a[child + 1])
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			Swap(a, child, parent);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

三、堆排序算法

有了向下调整算法后，可以尝试对任意数组排序，排序与大小堆刚好相反，排升序用大堆，排降序用小堆，现有数组{1,5,3,8,7,6},将其升序排列为{1,3,5,6,7,8};

排序先建堆，排升序建大堆

因为此时不再是除根结点外的堆结构，故应从最后一个叶子结点的父亲结点开始进行向下调整，图解如下：

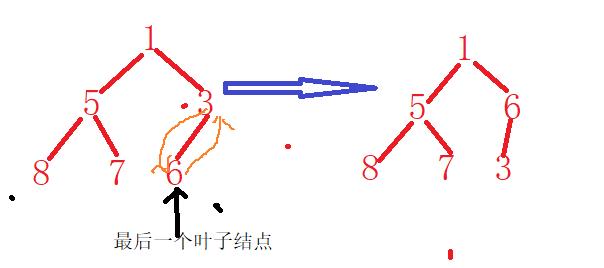
而后对每一个父亲结点进行调整



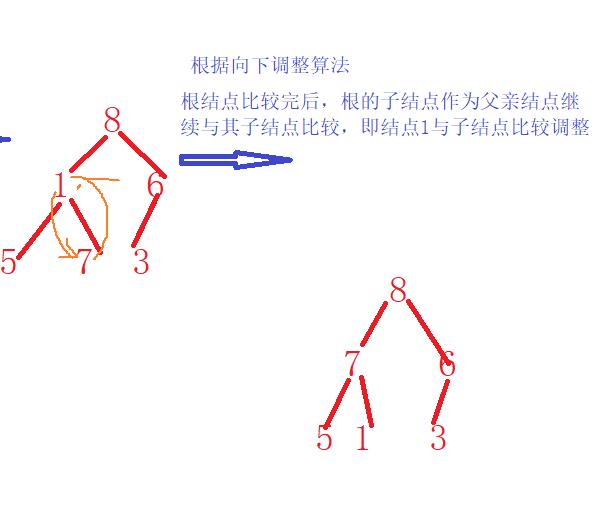
以上为建堆过程，建堆好以后进行升序排列，升序排列时不能破坏已经建好的堆的结构，即根结点不被破坏，所以可以对叶子结点进行调整

- 将根结点与最后一个叶子结点交换
- 除去最后一个叶子结点，用向下调整算法调整堆
- 直到最后一个单结点，排序完成

图示：


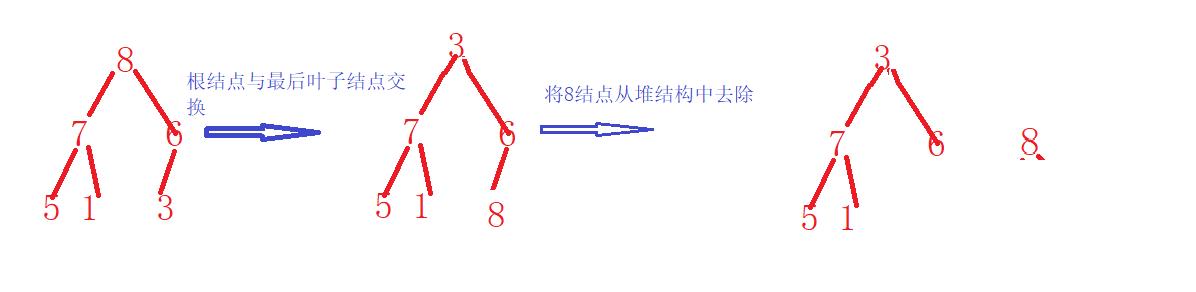
以此类推下去，选出{1,5,6,3}中的最大数6，接着选出{3,5,1}中的最大数5，其次是{1,3}中的最大数3，最后是1。
代码如下：

void Swap(int* a, int x, int y)
{
	int tmp = 0;
	tmp = a[x];
	a[x] = a[y];
	a[y] = tmp;
}
void Adjustdown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1< n && a[child] < a[child + 1])
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(a, child, parent);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void Heapsort(int* a, int n)
{
	//升序用大堆，找到最大后与最后一个换一下，再调整
	//降序用小堆，找到最小后与最后一个换一下，再调整
	int i = 0;
	for (i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		Adjustdown(a, n, i);
	}
	int end = n - 1;
	while (end > 0)
	{
		Swap(a, end, 0);
		Adjustdown(a, end, 0);
		--end;
	}
}
int main()
{
	int a[] = { 1,5,3,8,7,6 };
	//Adjustdown(a , sizeof(a)/sizeof(int),0);
	Heapsort(a,sizeof(a)/sizeof(int));
	int i = 0;
	for (i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		printf("%d ", a[i]);
	}
	return 0;
}