数据结构初阶第七篇——二叉树的顺序结构的应用（堆排序+TOPK问题）

Posted 2021-12-13 呆呆兽学编程

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构初阶第七篇——二叉树的顺序结构的应用（堆排序+TOPK问题）相关的知识，希望对你有一定的参考价值。

⭐️本篇博客我要来和大家一起聊一聊数据结构中的二叉树的顺序结构的两个应用——堆排序和TOPK问题
⭐️博客代码已上传至gitee：https://gitee.com/byte-binxin/data-structure/tree/master/Heap

🌏应用1——堆排序

🍇堆排序的概念及原理

⭐️堆排序：是指利用堆这种数据结构所设计的一种排序算法。堆排序通过建大堆或者小堆来进行排序的算法。

举个例子：给定我们一个数组{2, 3，4, 2，4，7}，我们可把这个数组在逻辑上看成是一种堆的结构，然后进行建堆，建大堆（或建小堆）我们就可以在堆顶选出一个最大（最小）的数，通过不断的选数，我们就可以把顺序弄出来了。
如何建堆？在上一篇博客中我已经跟大家说过了，就是这样的：

堆的构建有两种方法：
第一种：从第二个节点往后开始向上调整
第二种：从最后一个非叶子节点开始向下调整

第一种：从第二个叶子节点开始向上调整，把前面两个节点构成的堆建成大堆（小堆），如何依次调整第三个节点，第四个节点……直到调整最后一个，与堆的插入有些相似，只不过我们原来是有一组数，用一个动图给大家演示一下：

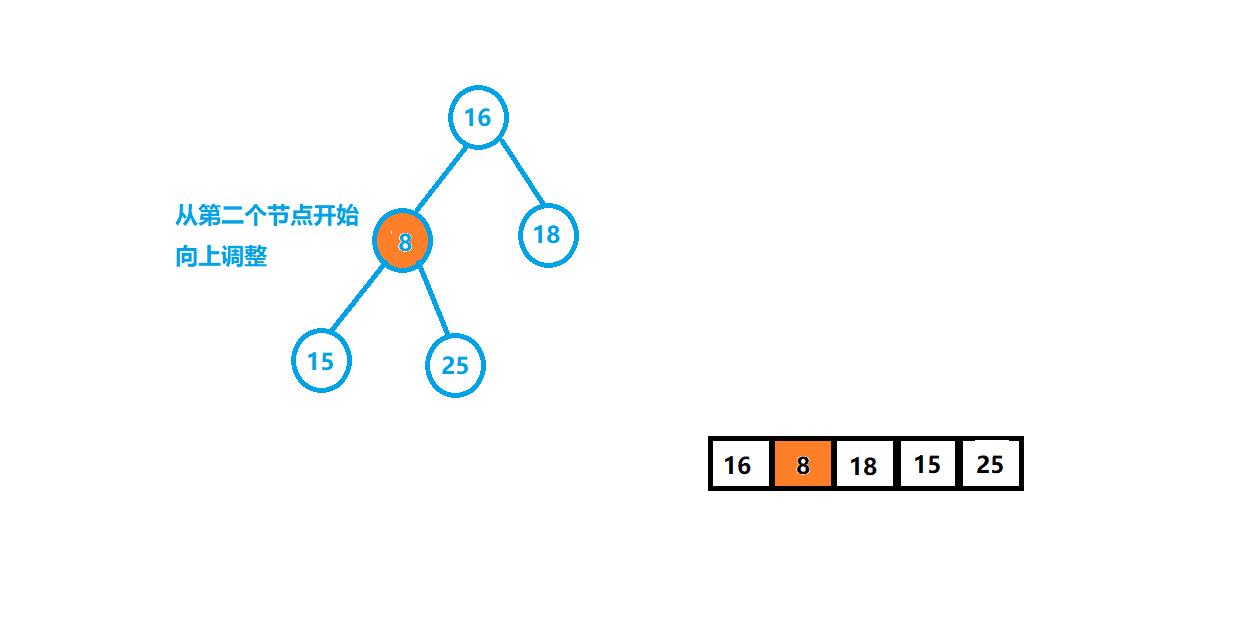
代码实现如下：

int i = 0;
//建小堆 排降序  建大堆 排升序
for (i = 1; i < n; i++)
{
	//建大堆 向下调整
	AdjustUp(hp->a, i);
}

第二种：从最后一个非叶子节点开始向下调整，从下往上，先把下面的子树建成大堆（小堆），最后就是堆顶向下调整了，看一下动图演示：

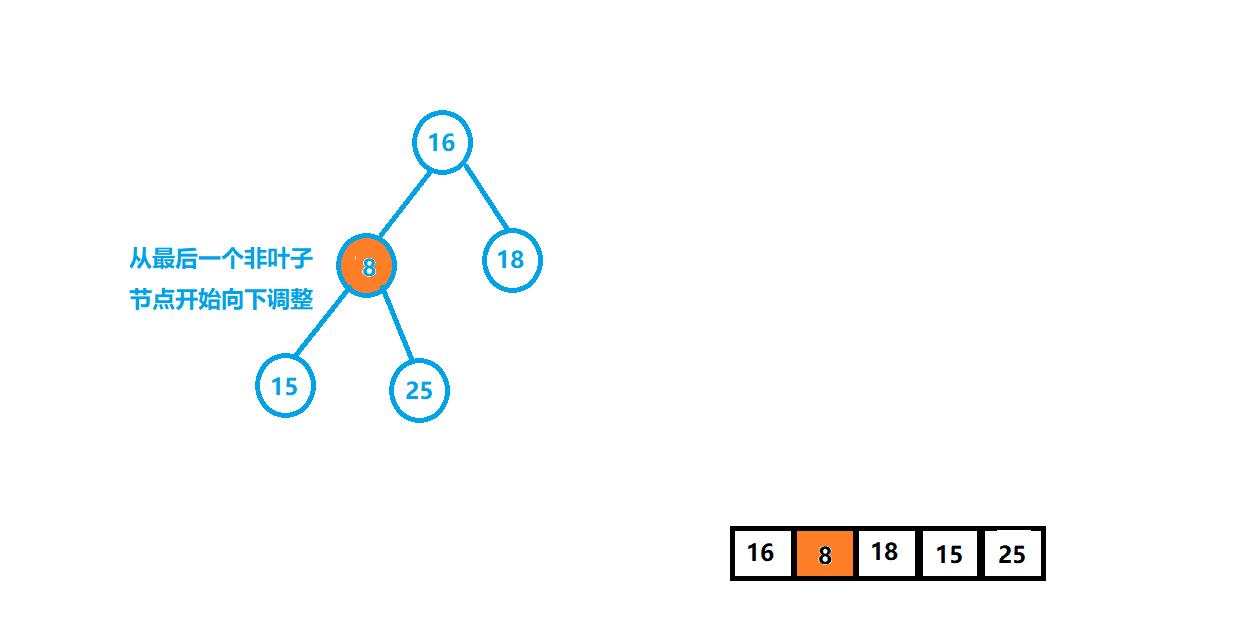
代码实现如下：

//找到最后一个父亲节点
int parent = (n - 1 - 1) / 2;
int i = 0;
//建小堆 排降序  建大堆 排升序
for (i = parent; i >= 0; i--)
{
	//建大堆 向下调整
	AdjustDown(hp->a, n, i);
}

🌾接下来，我们要考虑的一个问题是——排升序应该建大堆还是小堆？

不少人也许会说是建小堆，因为排升序第一个树肯定是最小的数，减小堆的话，堆顶就是最小的数，这看似有道理，其实不然，为什么呢？
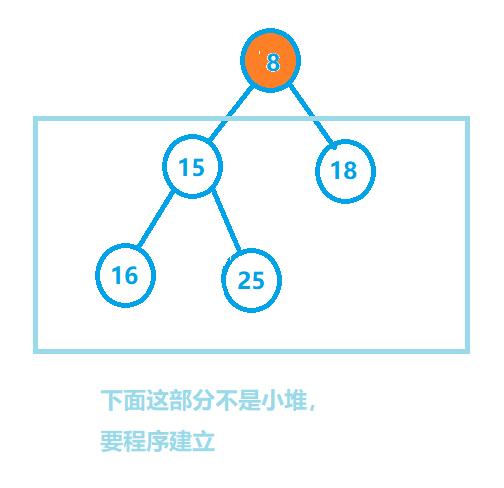
如果建小堆选数，选完第一个数之后，剩下的那些数就不能构成一个小堆了

建堆的时间复杂度是O(N)，每次重新建堆的话会是这个算法的时间复杂度变为O(n^2)，效率太低，那么堆排序也就失去了他存在的意义。

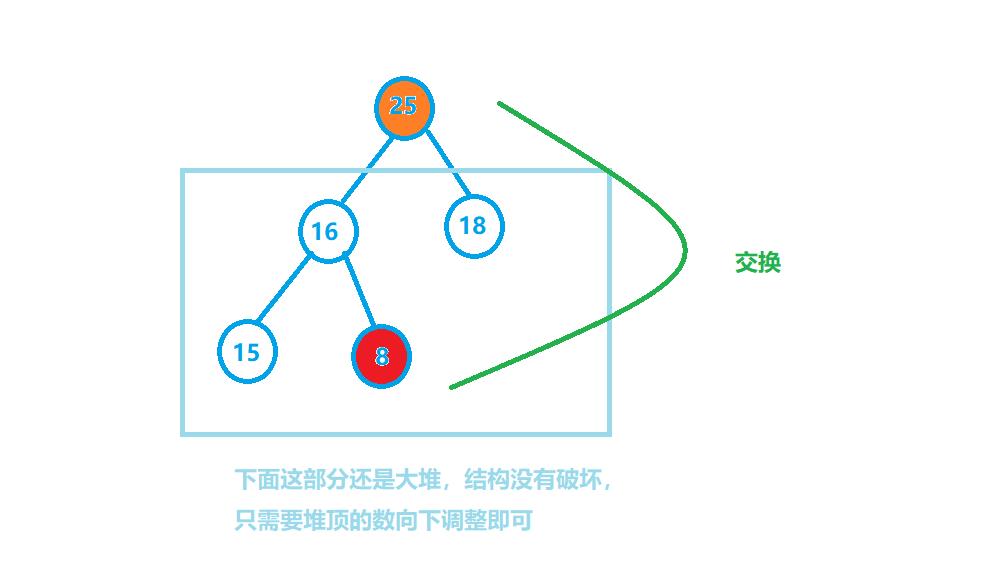
所以我们要建大堆，选出最大的数，然后与最后一个节点交换，如图

我们知道，向下调整的时间复杂度是O(logN)，所以建大堆才能显示出堆排序的优势。

🌴总结：排升序，建大堆，每次将堆顶的数与最后一个数交换，然后向下调整，（调整还没选出来的数）继续交换，直到选完最后一个数为止。

🍇堆排序的代码实现

具体代码实现如下：

void HeapSort(HPDataType* a, int n)
{
	//找到最后一个父亲节点
	int parent = (n - 1 - 1) / 2;
	int i = 0;
	//建小堆 排降序  建大堆 排升序
	for (i = parent; i >= 0; i--)
	{
		//建大堆 向下调整
		AdjustDown(a, n, i);
	}

	i = n - 1;
	while (i >= 0)
	{
		Swap(&a[0], &a[i]);
		AdjustDown(a, i, 0);
		i--;
	}
}

🍇堆排序时间复杂度分析

🌿这里时间复杂度分析分为两部分——建堆和n次向下调整
建堆：在上一篇博客中已经证明过了，时间复杂度是O(n)
n次向下调整：向下调整一次是O(logn)，n次就是O(n*logn)
nlogn+n≈nlogn
综上，堆排序时间复杂的是O(n*logn)

🌙应用2——TOPK问题

🍋TOPK问题的概念

🍬TOPK问题：找出N个数里面最大/最小的前K个问题。
例如：csdn热榜前10名，全国排名前10的李白。等等问题都是Topk问题。

🍋TOPK问题实现的原理

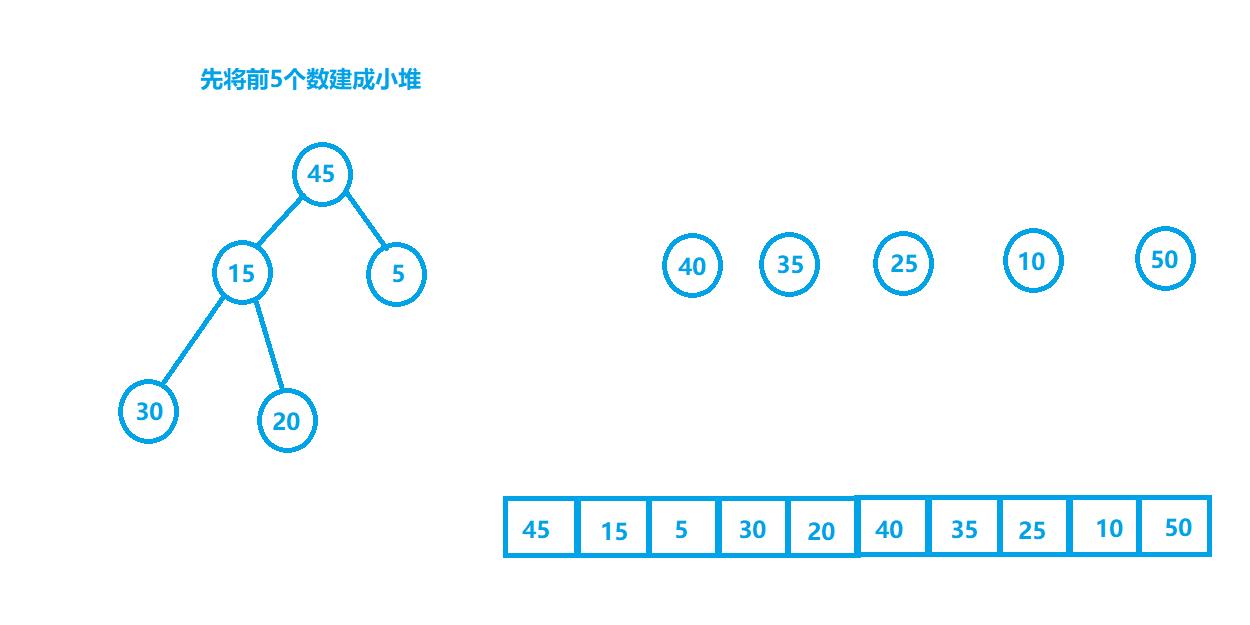
🍓原理：TOPK问题采用堆来实现，用一个大小为K的小堆，然后往堆顶插入数据，如果当前的数比堆顶的数大就把堆顶的数换下来并进行向下调整，否则就不做处理。
看一个动图演示（10选5）：

🍋TOPK问题的代码实现

代码实现如下：

void PrintTopK(int* a, int n, int k)
{
	assert(a);

	HP hp;
	HeapInit(&hp);
	//创建一个大小为k的堆
	HeapCreate(&hp, a, k);
	int i = 0;
	for (i = k; i < n; i++)
	{
		if (a[i] > HeapTop(&hp))
		{
			hp.a[0] = a[i];
			AdjustDown(hp.a, k, 0);
		}
	}
	HeapPrint(&hp);
	HeapDestory(&hp);
}