Pytorch Note49 Q-learning

Posted 2021-09-11 风信子的猫Redamancy

Pytorch Note49 Q-learning

文章目录

• Pytorch Note49 Q-learning
• • Q Learning 介绍
  • q-learning 的原理
  • • 状态和动作
    • Q-learning 算法
    • 单步演示

全部笔记的汇总贴： Pytorch Note 快乐星球

Q Learning 介绍

在增强学习中，有一种很有名的算法，叫做 q-learning，我们下面会从原理入手，然后通过一个简单的小例子讲一讲 q-learning。

q-learning 的原理

我们使用一个简单的例子来导入 q-learning，假设一个屋子有 5 个房间，某一些房间之间相连，我们希望能够走出这个房间，示意图如下

我们可以利用我们所学的图的知识，将其简化成一些节点和图的形式，每个房间作为一个节点，两个房间有门相连，就在两个节点之间连接一条线，可以得到下面的图片

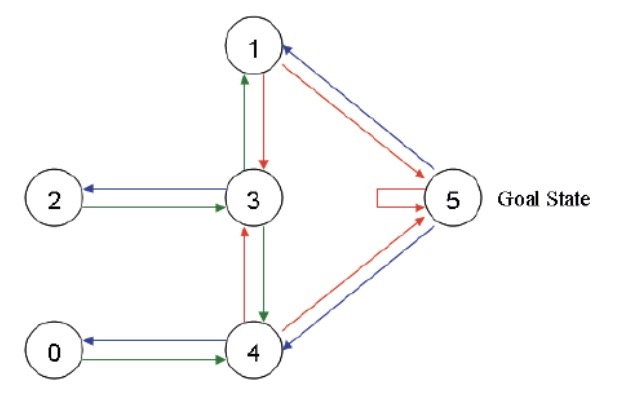
为了模拟整个过程，我们放置一个智能体在任何一个房间，希望它能够走出这个房间，也就是说希望其能够走到了 5 号节点。为了能够让智能体知道 5 号节点是目标房间，我们需要设置一些奖励，对于每一条边，我们都关联一个奖励值：直接连到目标房间的边的奖励值设置为 100，其他的边可以设置为 0，注意 5 号房间有一个指向自己的箭头，奖励值也设置为 100，其他直接指向 5 号房间的也设置为 100，这样当智能体到达 5 号房间之后，他就会选择一只待在 5 号房间，这也称为吸收目标，效果如下

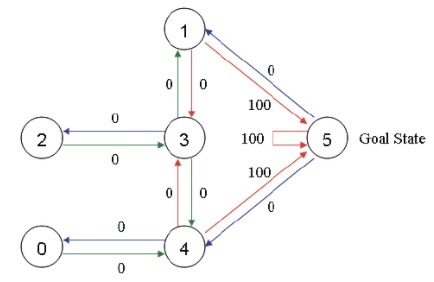
想想一下智能体可以不断学习，每次我们将其放在其中一个房间，然后它可以不断探索，根据奖励值走到 5 号房间，也就是走出这个屋子。比如现在这个智能体在 2 号房间，我们希望其能够不断探索走到 5 号房间。

状态和动作

q-learning 中有两个重要的概念，一个是状态，一个是动作，我们将每一个房间都称为一个状态，而智能体从一个房间走到另外一个房间称为一个动作，对应于上面的图就是每个节点是一个状态，每一个箭头都是一种行动。假如智能体处在状态 4，从状态 4 其可以选择走到状态 0，或者状态 3 或者状态 5，如果其走到了状态 3，也可以选择走到状态 2 或者状态 1 或者 状态 4。

我们可以根据状态和动作得到的奖励来建立一个奖励表，用 -1 表示相应节点之间没有边相连，而没有到达终点的边奖励都记为 0，如下

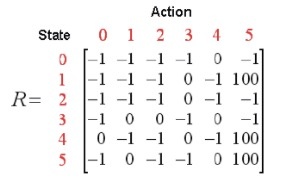
类似的，我们可以让智能体通过和环境的交互来不断学习环境中的知识，让智能体根据每个状态来估计每种行动可能得到的收益，这个矩阵被称为 Q 表，每一行表示状态，每一列表示不同的动作，对于状态未知的情景，我们可以随机让智能体从任何的位置出发，然后去探索新的环境来尽可能的得到所有的状态。刚开始智能体对于环境一无所知，所以数值全部初始化为 0，如下

我们的智能体通过不断地学习来更新 Q 表中的结果，最后依据 Q 表中的值来做决策。

Q-learning 算法

有了奖励表和 Q 表，我们需要知道智能体是如何通过学习来更新 Q 表，以便最后能够根据 Q 表进行决策，这个时候就需要讲一讲 Q-learning 的算法。

Q-learning 的算法特别简单，状态转移公式如下

Q ( s , a ) = R ( s , a ) + γ m a x a ~ { Q ( s ~ , a ~ ) } Q(s, a) = R(s, a) + \\gamma \\mathop{max}_{\\tilde{a}}\\{ Q(\\tilde{s}, \\tilde{a}) \\} Q(s,a)=R(s,a)+γmaxa~​{Q(s~,a~)}
其中 s, a 表示当前的状态和行动，$\tilde{s},\tilde{a}$ 分别表示 s 采取 a 的动作之后的下一个状态和该状态对应所有的行动，参数 $\gamma$ 是一个常数，$0 \\leq \\gamma \\le 1 $表示对未来奖励的一个衰减程度，形象地比喻就是一个人对于未来的远见程度。

解释一下就是智能体通过经验进行自主学习，不断从一个状态转移到另外一个状态进行探索，并在这个过程中不断更新 Q 表，直到到达目标位置，Q 表就像智能体的大脑，更新越多就越强。我们称智能体的每一次探索为 episode，每个 episode 都表示智能体从任意初始状态到达目标状态，当智能体到达一个目标状态，那么当前的 episode 结束，进入下一个 episode。

下面给出 q-learning 的整个算法流程

• step1 给定参数 $\gamma$ 和奖励矩阵 R
• step2 令 Q:= 0
• step3 For each episode:
  • 3.1 随机选择一个初始状态 s
  • 3.2 若未到达目标状态，则执行以下几步
    • （1）在当前状态 s 的所有可能行动中选取一个行为 a
    • （2）利用选定的行为 a，得到下一个状态 $\tilde{s}$
    • （3）按照前面的转移公式计算 Q(s, a)
    • （4）令 $s:=\tilde{s}$

单步演示

为了更好地理解 q-learning，我们可以示例其中一步。

首先选择 $\gamma =0.8$，初始状态为 1，Q 初始化为零矩阵

因为是状态 1，所以我们观察 R 矩阵的第二行，负数表示非法行为，所以下一个状态只有两种可能，走到状态 3 或者走到状态 5，随机地，我们可以选择走到状态 5。

当我们走到状态 5 之后，会发生什么事情呢？观察 R 矩阵的第 6 行可以发现，其对应于三个可能采取的动作：转至状态 1，4 或者 5，根据上面的转移公式，我们有

Q ( 1 , 5 ) = R ( 1 , 5 ) + 0.8 ∗ m a x { Q ( 5 , 1 ) , Q ( 5 , 4 ) , Q ( 5 , 5 ) } = 100 + 0.8 ∗ m a x { 0 , 0 , 0 } = 100 Q(1, 5) = R(1, 5) + 0.8 * max\\{Q(5, 1), Q(5, 4), Q(5, 5)\\} = 100 + 0.8 * max\\{0, 0, 0\\} = 100 Q(1,5)=R(1,5)+0.8∗max{Q(5,1),Q(5,4),Q(5,5)}=100+0.8∗max{0,0,0}=100

所以现在 Q 矩阵进行了更新，变为了

现在我们的状态由 1 变成了 5，因为 5 是最终的目标状态，所以一次 episode 便完成了，进入下一个 episode。

在下一个 episode 中又随机选择一个初始状态开始，不断更新 Q 矩阵，在经过了很多个 episode 之后，矩阵 Q 接近收敛，那么我们的智能体就学会了从任意状态转移到目标状态的最优路径。

从上面的原理，我们知道了 q-learning 最重要的状态转移公式，这个公式也叫做 Bellman Equation，通过这个公式我们能够不断地进行更新 Q 矩阵，最后得到一个收敛的 Q 矩阵。

下面我们通过代码来实现这个过程

我们定义一个简单的走迷宫过程，也就是

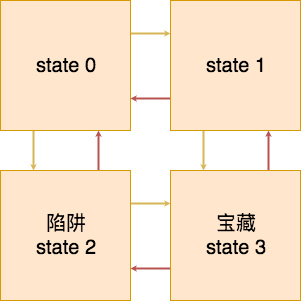
初始位置随机在 state 0， state 1 和 state 2 上，然后希望智能体能够走到 state 3 获得宝藏，上面可行的行动路线已经用箭头标注了

import numpy as np
import random

下面定义奖励矩阵，一共是 4 行，5 列，每一行分别表示 state 0 到 state 3 这四个状态，每一列分别表示上下左右和静止 5 种状态，奖励矩阵中的 0 表示不可行的路线，比如第一个行，上走和左走都是不可行的路线，都用 0 表示，向下走会走到陷阱，所以使用 -10 表示奖励，向右走和静止都给与 -1 的奖励，因为既没有触发陷阱，也没有到达宝藏，但是过程中浪费了时间。

reward = np.array([[0, -10, 0, -1, -1],
                   [0, 10, -1, 0, -1],
                   [-1, 0, 0, 10, -10],
                   [-1, 0, -10, 0, 10]])

接下来定义一个初始化为 0 的 q 矩阵

q_matrix = np.zeros((4, 5))

然后定义一个转移矩阵，也就是从一个状态，采取一个可行的动作之后到达的状态，因为这里的状态和动作都是有限的，所以我们可以将他们存下来，比如第一行表示 state 0，向上和向左都是不可行的路线，所以给 -1 的值表示，向下走到达了 state 2，所以第二个值为 2，向右走到达了 state 1，所以第四个值是 1，保持不同还是在 state 0，所以最后一个标注为 0，另外几行类似。

transition_matrix = np.array([[-1, 2, -1, 1, 0],
                              [-1, 3, 0, -1, 1],
                              [0, -1, -1, 3, 2],
                              [1, -1, 2, -1, 3]])

最后定义每个状态的有效行动，比如 state 0 的有效行动就是下、右和静止，对应于 1，3 和 4

valid_actions = np.array([[1, 3, 4],
                          [1, 2, 4],
                          [0, 3, 4],
                          [0, 2, 4]])

# 定义 bellman equation 中的 gamma
gamma = 0.8

最后开始让智能体与环境交互，不断地使用 bellman 方程来更新 q 矩阵，我们跑 10 个 episode

for i in range(10):
    start_state = np.random.choice([0, 1, 2], size=1)[0] # 随机初始起点
    current_state = start_state
    while current_state != 3: # 判断是否到达终点
        action = random.choice(valid_actions[current_state]) # greedy 随机选择当前状态下的有效动作
        next_state = transition_matrix[current_state][action] # 通过选择的动作得到下一个状态
        future_rewards = []
        for action_nxt in valid_actions[next_state]:
            future_rewards.append(q_matrix[next_state][action_nxt]) # 得到下一个状态所有可能动作的奖励
        q_state = reward[current_state][action] + gamma * max(future_rewards) # bellman equation
        q_matrix[current_state][action] = q_state # 更新 q 矩阵
        current_state = next_state # 将下一个状态变成当前状态
        
    print('episode: {}, q matrix: \\n{}'.format(i, q_matrix))
    print()

episode: 0, q matrix: 
[[ 0.  0.  0.  0.  0.]
 [ 0. 10.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.]]

episode: 1, q matrix: 
[[  0. -10.   0.   0.  -1.]
 [  0.  10.   0.   0.   0.]
 [ -1.   0.   0.  10.   0.]
 [  0.   0.   0.   0.   0.]]

episode: 2, q matrix: 
[[  0. -10.   0.   7.  -1.]
 [  0.  10.  -1.   0.   7.]
 [ -1.   0.   0.  10.   0.]
 [  0.   0.   0.   0.   0.]]

episode: 3, q matrix: 
[[  0.  -10.    0.    7.   -1. ]
 [  0.   10.    4.6   0.    7. ]
 [  4.6   0.    0.   10.    0. ]
 [  0.    0.    0.    0.    0. ]]

episode: 4, q matrix: 
[[ 0.  -2.   0.   7.   4.6]
 [ 0.  10.   4.6  0.   7. ]
 [ 4.6  0.   0.  10.  -2. ]
 [ 0.   0.   0.   0.   0. ]]

episode: 5, q matrix: 
[[ 0.  -2.   0.   7.   4.6]
 [ 0.  10.   4.6  0.   7. ]
 [ 4.6  0.   0.  10.  -2. ]
 [ 0.   0.   0.   0.   0. ]]

episode: 6, q matrix: 
[[ 0.  -2.   0.   7.   4.6]
 [ 0.  10.   4.6  0.   7. ]
 [ 4.6  0.   0.  10.  -2. ]
 [ 0.   0.   0.   0.   0. ]]

episode: 7, q matrix: 
[[ 0.  -2.   0.   7.   4.6]
 [ 0.  10.   4.6  0.   7. ]
 [ 4.6  0.   0.  10.  -2. ]
 [ 0.   0.   0.   0.   0. ]]

episode: 8, q matrix: 
[[ 0.  -2.   0.   7.   4.6]
 [ 0.  10.   4.6  0.   7. ]
 [ 4.6  0.   0.  10.  -2. ]
 [ 0.   0.   0.   0.   0. ]]

episode: 9, q matrix: 
[[ 0.  -2.   0.   7.   4.6]
 [ 0.  10.   4.6  0.   7. ]
 [ 4.6  0.   0.  10.  -2. ]
 [ 0.   0.   0.   0.   0. ]]

可以看到在第一次 episode 之后，智能体就学会了在 state 2 的时候向下走能够得到奖励，通过不断地学习，在 10 个 episode 之后，智能体知道，在 state 0，向右走能得到奖励，在 state 1 向下走能够得到奖励，在 state 3 向右 走能得到奖励，这样在这个环境中任何一个状态智能体都能够知道如何才能够最快地到达宝藏的位置

从上面的例子我们简单的演示了 q-learning，可以看出自己来构建整个环境是非常麻烦的，所以我们可以通过一些第三方库来帮我们搭建强化学习的环境，其中最有名的就是 open-ai 的 gym 模块，下一章我们将介绍一下 gym。