0x56. 动态规划 - 状态压缩DP（习题详解 × 7）

Posted 2021-09-08 繁凡さん

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了0x56. 动态规划 - 状态压缩DP（习题详解 × 7）相关的知识，希望对你有一定的参考价值。

本系列博客是《算法竞赛进阶指南》的学习笔记，包含书中的部分重要知识点、例题解题报告及我个人的学习心得和对该算法的补充拓展，仅用于学习交流和复习，无任何商业用途。博客中部分内容来源于书本和网络，由我个人整理总结。部分内容由我个人编写而成，如果想要有更好的学习体验或者希望学习到更全面的知识，请于京东搜索购买正版图书：《算法竞赛进阶指南》——作者李煜东，强烈安利，好书不火系列，谢谢配合。

学习笔记目录链接： 学习笔记目录链接

整理的算法模板合集： ACM模板

点我看算法全家桶系列！！！

文章目录

动态规划算法的过程是随着阶段的增长，在每个状态维度上的分界点组成了DP拓展的轮廓。对于某些问题，我们需要在动态规划的状态中记录一个集合，保存这个轮廓的详细信息，以便于进行状态转移。若集合大小不超过 $N$ ，集合中每个元素都是小于 $k$ 的自然数，则我们可以把这个集合看做一个 $N$ 位 $k$ 进制数，以一个 $0,k^N-1]$ 之间的十进制整数的形式作为DP状态的一维。这种把集合转化为整数记录在DP状态中的一类算法被称之为状态压缩动态规划算法。

Problem A. 最短Hamilton路径

AcWing 91

给定一张 $n$ 个点的带权无向图，点从 $0\\sim n−1$ 标号，求起点 $0$ 到终点 $n - 1$ 的最短 Hamilton 路径。

Hamilton 路径的定义是从 $0$ 到 $n - 1$ 不重不漏地经过每个点恰好一次。

$1≤n≤20, 0≤a[i,j]≤10^7$

Solution

如果直接爆搜的话时间复杂度为 $O(20\\times 20!)$ ，考虑优化。

考虑状态DP，整个状态空间可以看作 $N$ 维，每维代表一个结点，只有 $0$ （表示尚未访问过），1（已访问过）两个值， $k = 2$ ，我们可以使用二进制数 $k^N$ 代表整个状态空间的所有集合，以访问过的结点数目为阶段，从 $(0,0,0\\dots,0)$ 到 $(1,1,\\dots,1)$ 表示 $N$ 个结点的状态。我们使用 $N$ 位 $k$ 进制数， $0,2^N-1]$ 之间的十进制整数存储结点的访问情况。为了知道最后经过的结点是哪一个，我们把该结点编号整数作为附加信息，同样保存在 DP 的状态中。

有转移方程：

$f[\\mathrm{state},j] = \\min\\{f[\\mathrm{state}_k,k]+\\mathrm{weight}[k,j]\\}$

其中 $\\mathrm{state}$ 表示当前的状态， $\\mathrm{state}_k$ 表示 $\\mathrm{state}$ 去掉结点 $j$ 点后， $k$ 的状态，当前的状态在 $j$ 点的时候的最短路就等于从状态的结点 $k$ 转移到结点 $j$ 加上 $k$ 到 $j$ 的距离。

初始化： $f [1, 0] = 0$ ，其余为正无穷。

目标： $f[2^n-1,n-1]$

Code

#include <bits/stdc++.h>
using namespace std;
const int maxn = 21;
int f[1 << maxn][maxn];
int n, m, s, t, k, ans;
int w[maxn << 1][maxn << 1];
int main()
{
    cin >> n;
    for (int i = 0; i < n; ++ i) 
        for (int j = 0; j < n; ++ j) 
            scanf("%d", &w[i][j]);
    memset(f, 0x3f, sizeof f);
    f[1][0] = 0;
    for (int i = 0; i <= (1 << n) - 1; ++ i) {
        for (int j = 0; j < n; ++ j) {
            if ((i >> j) & 1) {
                for (int k = 0; k < n; ++ k) {
                    int now = i ^ (1 << j);
                    if ((now >> k) & 1)
                        f[i][j] = min(f[i][j], f[now][k] + w[k][j]);
                }
            }
        }
    }
    cout << f[(1 << n) - 1][n - 1] << '\\n';
    return 0;
}

ProblemB. 蒙德里安的梦想

AcWing 291

求把 $N \times M$ 的棋盘分割成若干个 $1 \times 2$ 的的长方形，有多少种方案。

例如当 $N = 2$ ， $M = 4$ 时，共有 $5$ 种方案。当 $N = 2$ ， $M = 3$ 时，共有 $3$ 种方案。

Solution

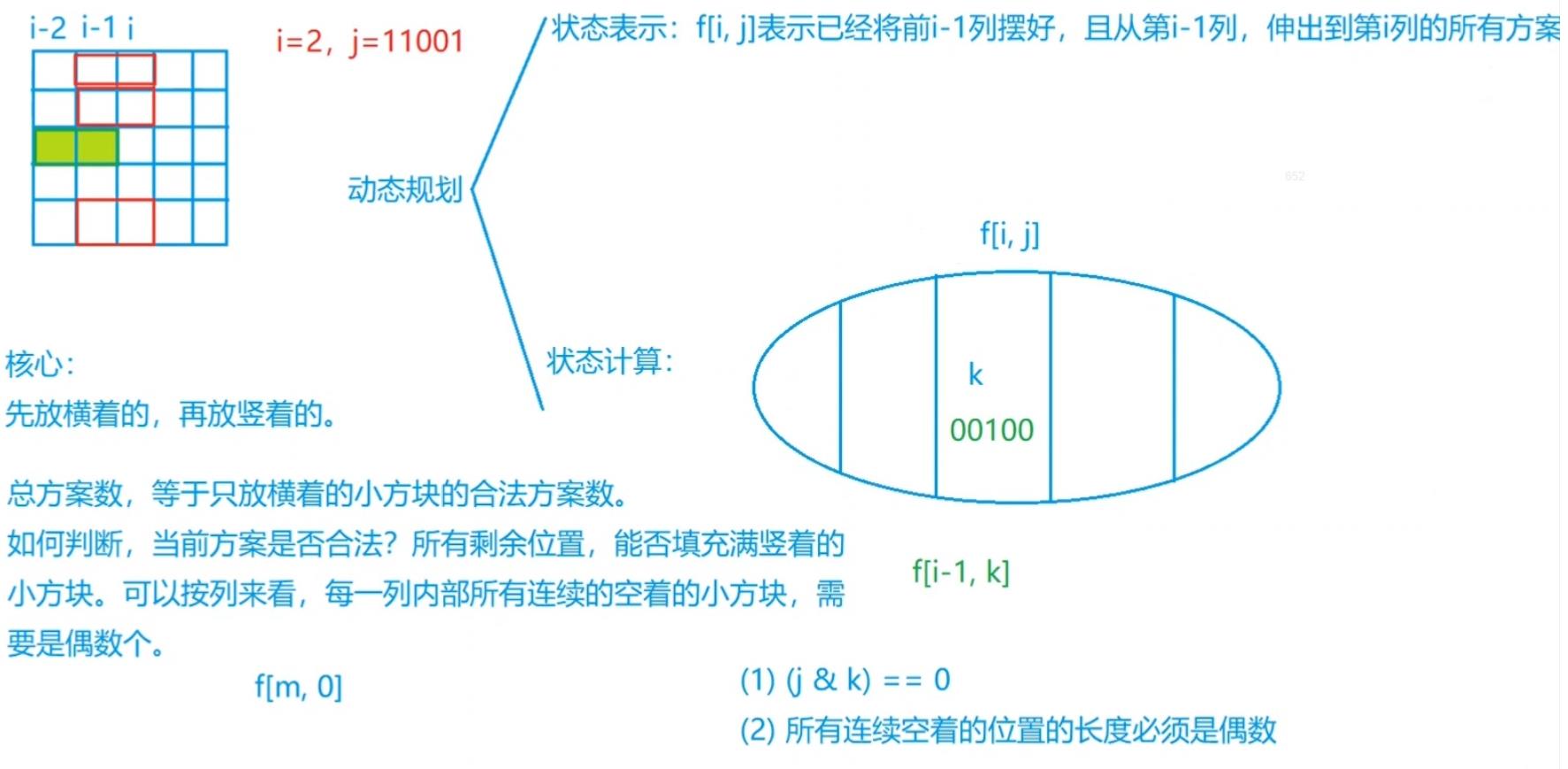
棋盘性的状态压缩DP，考虑以行为阶段，当前第 $i$ 行内每个格子的状态显然只有两种：

对下一行没有影响，即 $1\\times 2$ 的长方形在本行已结束
对下一行有影响，即 $1\\times 2$ 的长方形在本行竖着放，占一格，下一行占一格。

每行只有 $m\\le 11$ 列，每个格子只有两个状态，我们显然可以使用 $m$ 位 $k = 2$ 进制数 $j$ 表示当前行所有格子的状态。

因此我们设 $f [i, j]$ 表示第 $i$ 行的所有格子的状态为 $j$ 时，前 $i$ 行分割方案的总数。

显然第 $i - 1$ 行的状态 $k$ 转移到第 $i$ 行的状态 $j$ ，当且仅当：

j & k = 0
二进制数 j | k 中，每段连续的 $0$ 都必须有偶数个，对应着图中横着放置的 $1\\times 2$ 的长方形。

我们可以直接预处理处 $0,2^n-1]$ 中所有满足条件二的二进制数转换的十进制整数集合 $S$ ，枚举的时候判断 j | k 是否在集合 $S$ 中即可。

Code

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int maxn = 12;
int n, m, t, k, ans;
ll f[maxn][1 << maxn];
bool s[1 << maxn];

int main()
{
    while (scanf("%d%d", &n, &m) != EOF && n | m) { 
        for (int i = 0; i < 1 << m; ++ i) {
            bool cnt = false, odd = false;
            for (int j = 0; j < m; ++ j) 
                if((i >> j) & 1)
                    odd |= cnt, cnt = 0x54. 动态规划 - 树形DP（习题详解 × 12）
 0x53. 动态规划 - 区间DP（习题详解 × 8）
 0x52. 动态规划 - 背包（习题详解 × 19）
 动态规划区间计数数位统计状态压缩树形DP与记忆化搜索 题解与模板
 0x55. 动态规划 - 环形与后效性处理（例题详解 × 6）
 dp状态压缩