牛客Top200---最长递增子序列（求子序列+长度 画图详解java）

Posted 2021-09-08 小样5411

题目

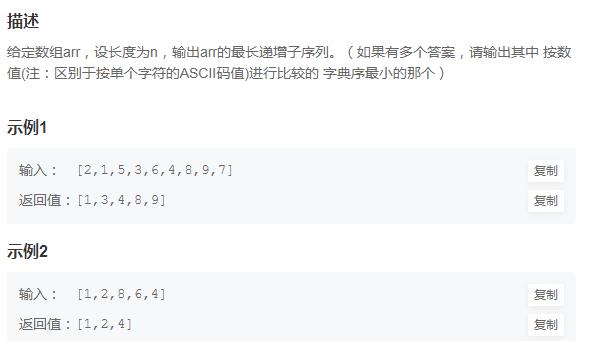
注意：这里字典序最小，直接看有点不好充分理解，等你看完整个解析就懂了

解析

解此题要用两个数组，一个temp数组用于记录递增子序列，还需要一个长度数组dp，记录新增的元素后数组的长度，可以用示例1画图给大家解释
首先，先把arr[0]放进temp数组中，后面添加规则是新增元素e和temp中最后一位比较
1、若e>arr[i]，则直接添加到结尾
2、若e=arr[i]，则不添加
3、若e<arr[i]，则e将替换temp数组中第一个比e大的元素
具体如下图

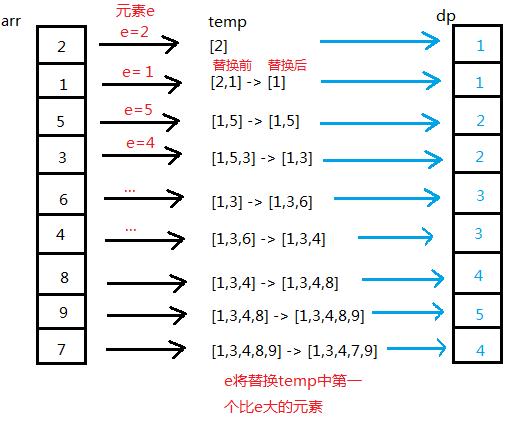
在 dp 数组中标完号后，为了满足题目要求的字典序最小，我们需要从后往前遍历，长度从大到小，倒着填入 LCS 中，只有这样才满足题意所指的字典序最小，才能得到最长递增子序列，最后我们获得结果 LCS。

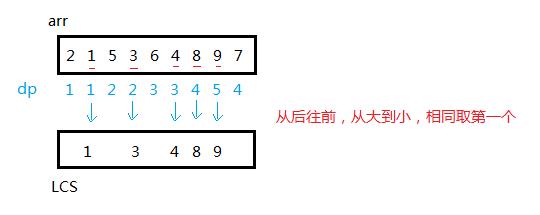
注意：查找第一个比新增元素e大的位置时，用的是二分法，整个算法时间复杂度为nlogn，可以画图说明下

以temp=[1,3,4,8,9]为例，要新增元素e=7的时候为例，结果应该是[1,3,4,7,9]，替换第一个比e大的，也就是8
二分法代码如下，key为新增的元素，此处为7，len为temp数组长度

public int findFirstIndex(int[] temp, int len, int key){
        int left = 0;
        int right = len-1;
        while(left <= right){
            int mid = (left + right) / 2;
            if(temp[mid] < key){
                left = mid + 1;
            }else{
                right = mid - 1;
            }
        }
      return left;
}

代码

综上详细解析后，我们就可以清晰的写出实际的代码了，初始需要两个数组，分别是temp和dp，数组大小和arr一样，并且要声明一个变量名为len的整型变量，用于记录temp在新增元素的过程中长度变化，从而记录在dp数组中。初始时，先放arr[0]进入temp，然后再进行遍历，遵循上面说的原则，大于小于等于三种情况，需要替换时则调用二分法获取需要替换的位置（下标），然后进行替换。

注：上面给出的是求最长递增子序列，其长度可以直接res.length，直接获取子序列长度即可

import java.util.*;


public class Solution {
    /**
     * retrun the longest increasing subsequence
     * @param arr int整型一维数组 the array
     * @return int整型一维数组
     */
    public int[] LIS (int[] arr) {
        if(arr.length <= 1 || arr == null) return arr;
        int[] temp = new int[arr.length];
        int[] dp = new int[arr.length];
        temp[0] = arr[0];//先将arr[0]放入temp
        int len = 1;//temp已经有一个arr[0]，所以len=1
        dp[0] = len;//记录temp的初始长度
        for(int i=1 ; i < arr.length ; i++){
            //arr[i]表示元素e，是否大于temp最后一位元素，大于则直接放最后，len++
            //循环结束时，len记录的是替换过程中最大的长度，即最大递增子序列
            if(temp[len-1] < arr[i]){
                temp[len++] = arr[i];
                dp[i] = len;//记录temp数组长度
            }else if(temp[len-1] == arr[i]){
                dp[i] = len;//记录temp数组长度
            }else{
                // 利用二分法，替换第一个大于arr[i]的元素
                int index = findFirstIndex(temp, len, arr[i]);
                temp[index] = arr[i];
                dp[i] = (index+1);//记录形成的新子序列的长度
            }
        }
        //得到最长递增子序列res
        int[] res = new int[len];
        //从后往前，长度len从大到小遍历
        for(int i=arr.length-1; i>=0; i--){
            if(dp[i] == len){
                res[--len] = arr[i];
            }
        }
        return res;
    }
    
    //查找第一个大于元素位置，如新增7的时,temp=[1,3,4,8,9],len=5,key=7
    public int findFirstIndex(int[] temp, int len, int key){
        int left = 0;
        int right = len-1;
        while(left <= right){
            int mid = (left + right) / 2;
            if(temp[mid] < key){
                left = mid + 1;
            }else{
                right = mid - 1;
            }
        }
        return left;
    }
}