Pytorch学习笔记3.深度学习基础
Posted 贪钱算法还我头发
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Pytorch学习笔记3.深度学习基础相关的知识,希望对你有一定的参考价值。
文章目录
根据龙良曲Pytorch学习视频整理,视频链接:
【计算机-AI】PyTorch学这个就够了!
(好课推荐)深度学习与PyTorch入门实战——主讲人龙良曲
13.梯度
- 导数 derivative
- 偏微分 partial derivate
- 梯度 gradient(向量)
How to search for minima?
- θ t + 1 = θ t − α t ▽ f ( θ t ) \\theta_{t+1}=\\theta_t-\\alpha_t\\triangledown f(\\theta_t) θt+1=θt−αt▽f(θt)
Optimizer performance
- initialization status 何恺明初始化方法
- learning rate (learning_rate_decay)
- momentum
14.激活函数
- 连续不可导
- Sigmoid / Logistic
σ
′
=
σ
(
1
−
σ
)
\\sigma'=\\sigma(1-\\sigma)
σ′=σ(1−σ)
torch.sigmoid()
F.sigmoid() (import torch.nn.functional as F) - Tanh
torch.tanh() - Relu
torch.relu()
F.relu() (import torch.nn.functional as F)
Typical Loss
- Mean Squared Error
MSE l o s s = ∑ [ y − ( x w + b ) ] 2 loss = \\sum [y-(xw+b)]^2 loss=∑[y−(xw+b)]2
L 2 − n o r m = ∣ ∣ y − ( x w + b ) ∣ ∣ 2 L2-norm=||y-(xw+b)||_2 L2−norm=∣∣y−(xw+b)∣∣2 - Cross Entropy Loss
binary
multi-class
+softmax
Leave it to Logistic Regression Part - Softmax
soft version of max
S ( y i ) = e y i ∑ j e y j S(y_i)=\\frac{e^{y_i}}{\\sum_je^{y_j}} S(yi)=∑jeyjeyi
∂ p i ∂ p j = { p i ( 1 − p i ) i = j − p j ∗ p i i ≠ j \\frac{\\partial p_i}{\\partial p_j}=\\left\\{\\begin{matrix} p_i(1-p_i)&i=j \\\\ -p_j*p_i& i\\neq j \\end{matrix}\\right. ∂pj∂pi={pi(1−pi)−pj∗pii=ji=j
Gradient API
torch.autograd.grad(loss, [w1, w2,...])loss.backward()
import torch
import torch.nn.functional as F
x = torch.ones(1)
w = torch.full([1], 2.)
mse = F.mse_loss(torch.ones(1), x*w)
print(mse) # tensor(1., grad_fn=<MseLossBackward>)
# torch.autograd.grad(mse, [w]) # RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn
print(w.requires_grad_()) # tensor([2.], requires_grad=True)
# print(torch.autograd.grad(mse, [w])) # 动态图未更新会报错RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn
mse = F.mse_loss(torch.ones(1), x*w)
# print(torch.autograd.grad(mse, [w])) # (tensor([2.]),
mse.backward()
print(w.grad) # tensor([2.])
a = torch.rand(3, requires_grad=True)
print(a) # tensor([0.0377, 0.4542, 0.1386], requires_grad=True)
p = F.softmax(a, dim=0)
# p.backward() # 报错 RuntimeError: grad can be implicitly created only for scalar outputs
# retain_graph=True 不会清除计算图
print(torch.autograd.grad(p[0], [a], retain_graph=True)) # (tensor([ 0.1998, -0.1156, -0.0843]),)
print(torch.autograd.grad(p[1], [a], retain_graph=True)) # (tensor([-0.1156, 0.2434, -0.1278]),)
print(torch.autograd.grad(p[2], [a], retain_graph=True)) # (tensor([-0.0843, -0.1278, 0.2121]),)
15.感知机
单一输出感知机求导

∂
E
∂
w
j
0
=
(
O
0
−
t
)
O
0
(
1
−
O
0
)
x
j
0
\\frac{\\partial E}{\\partial w_{j0}}=(O_0-t)O_0(1-O_0)x^0_j
∂wj0∂E=(O0−t)O0(1−O0)xj0
多输出Loss层 (Multi-output Perception)
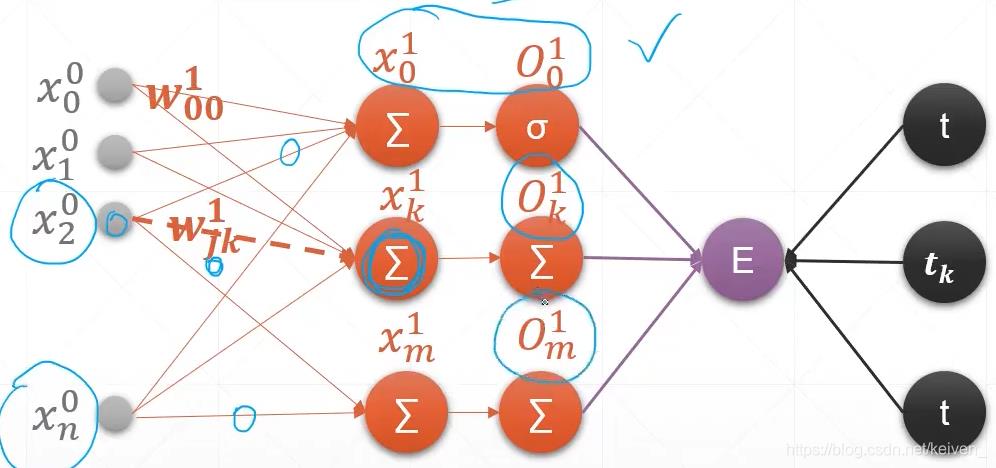
∂
E
∂
w
j
k
=
(
O
k
−
t
k
)
O
k
(
1
−
O
k
)
x
j
0
\\frac{\\partial E}{\\partial w_{jk}}=(O_k-t_k)O_k(1-O_k)x^0_j
∂wjk∂E=(Ok−tk)Ok(1−Ok)xj0
import torch
import torch.nn.functional as F
x = torch.randn(1, 10)
# w = torch.randn(1, 10, requires_grad=True) # 单一层感知机
w = torch.randn(2, 10, requires_grad=True) # 多输出Loss层
o = torch.sigmoid(x@w.t())
print(o.shape) # torch.Size([1, 2])
loss = F.mse_loss(torch.ones(1, 1), o) # broadcasting
print(loss.shape) # torch.Size([])
print(loss) # tensor(0.2094, grad_fn=<MseLossBackward>)
loss.backward()
print(w.grad)
"""
tensor([[-2.0498e-01, 2.4619e-02, -8.0208e-04, -1.3723e-01, -1.3014e-01,
-1.4648e-01, -7.5119e-02, 4.9381e-02, 2.7161e-01, 4.8075e-02],
[-4.8705e-03, 5.8495e-04, -1.9058e-05, -3.2607e-03, -3.0922e-03,
-3.4804e-03, -1.7849e-03, 1.1733e-03, 6.4536e-03, 1.1423e-03]])
"""
16.链式法则
import torch
import torch.nn.functional as F
x = torch.tensor(1.)
w1 = torch.tensor(2., requires_grad=True)
b1 = torch.tensor(1.)
w2 = torch.tensor(2., requires_grad=True)
b2 = torch.tensor(1.)
y1 = x * w1 + b1
y2 = y1 * w2 + b2
dy2_dy1 = torch.autograd.grad(y2, [y1], retain_graph=True)[0]
dy1_dw1 = torch.autograd.grad(y1, [w1], retain_graph=True)[0]
dy2_dw1 = torch.autograd.grad(y2, [w1], retain_graph=True)[0]
print(dy2_dy1 * dy1_dw1) # tensor(2.)
print(dy2_dw1) # tensor(2.)
17.反向传播
For an output layer node k ∈ \\in ∈ K ∂ E ∂ W j k = O j δ k \\frac{\\partial E}{\\partial W_{jk}}=O_j\\delta_k ∂Wjk∂E=Ojδk
where
δ
k
=
O
k
(
1
−
O
k
)
(
O
k
−
t
k
)
\\delta _k = O_k(1-O_k)(O_k-t_k)
δk 以上是关于Pytorch学习笔记3.深度学习基础的主要内容,如果未能解决你的问题,请参考以下文章 「深度学习一遍过」必修18:基于pytorch的语义分割模型实现