C/C++语言数据结构快速入门(代码解析+内容解析)特殊矩阵
Posted 蓝盒子bluebox
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了C/C++语言数据结构快速入门(代码解析+内容解析)特殊矩阵相关的知识,希望对你有一定的参考价值。
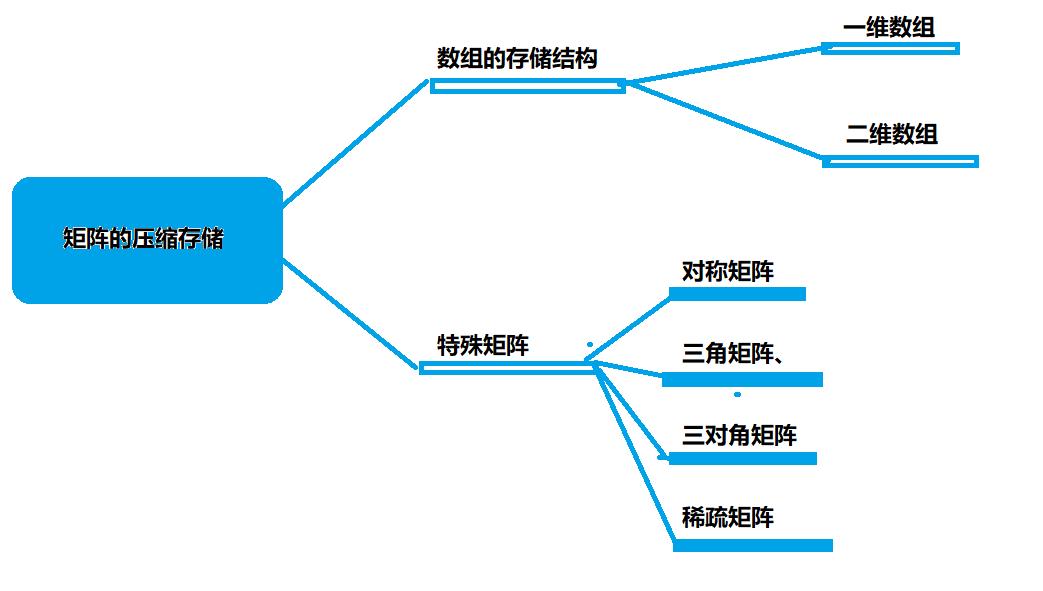
一、压缩矩阵
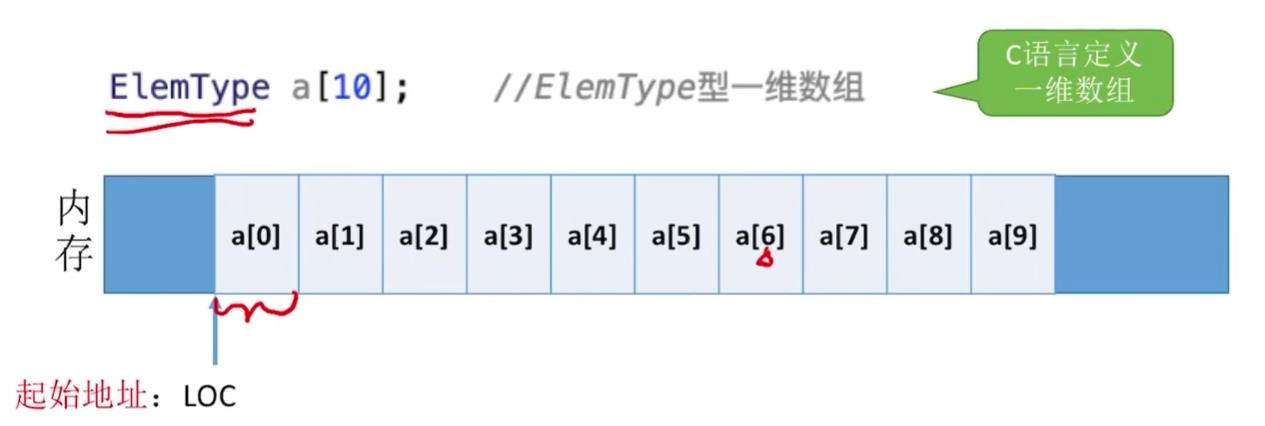
1、一维数组的存储结构
ElemType a[10]; //ElemType型一维数组

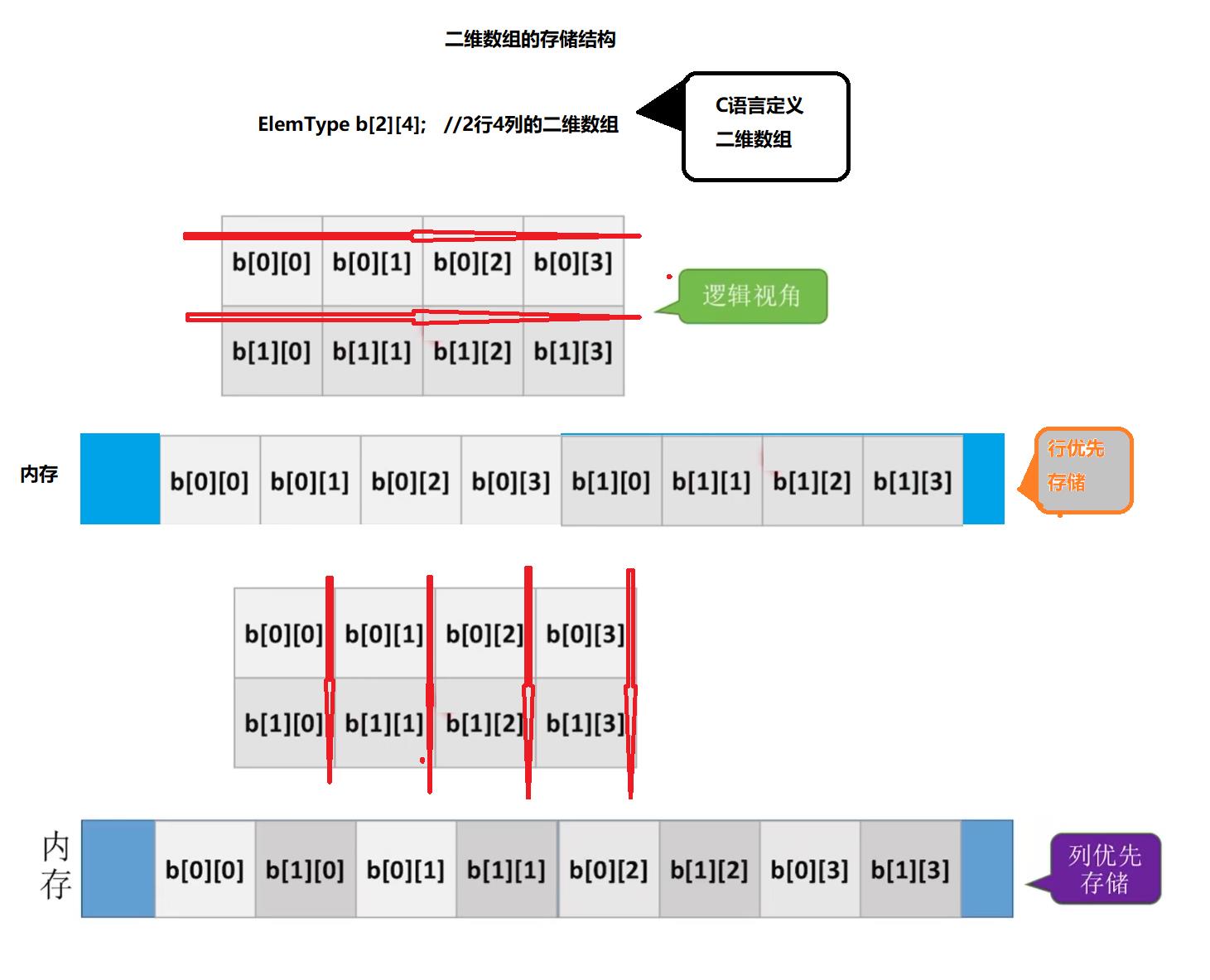
(1)计算上述第一种方式行优先存储,计算某个元素的地址

M行N列的二维数组b[M][N]中,如果按照行优先存储,则b[i][j]的存储地址=LOC +(i * N + j) * sizeof(ElemType)
例如上方的数据计算b[1][2]的存储地址 为LOC + 6 *sizeof(ElemType)
(2)采用列优先存储二维数组
M行N列的二维数组b[M][N]中,若按列优先存储,则b[i][j]的存储地址 = LOC + (j * M + i) * sizeof(ElemType)

b[1][2]的地址:= LOC + 5 * sizeof(ElemType)
2、普通矩阵的存储(直接使用二维数组存储即可)
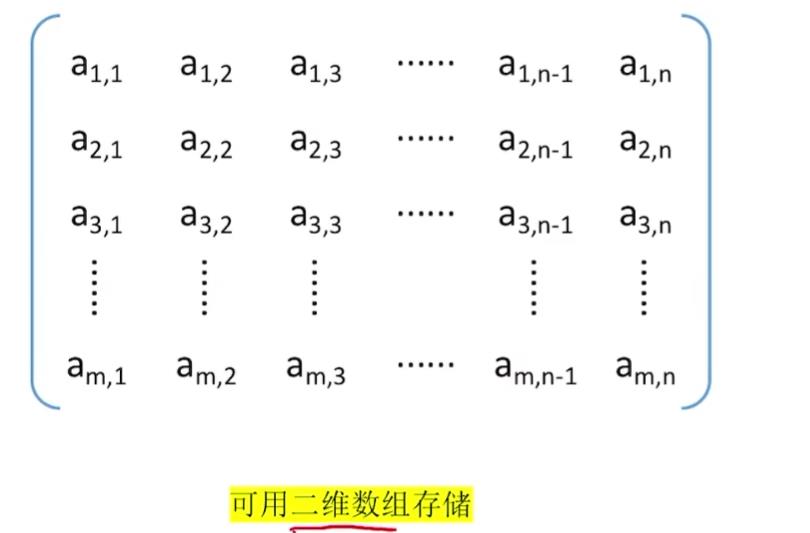
注意:描述矩阵元素的时候,行、列通常从1开始;而描述数组时通常下标从1开始;而描述数组时通常下标从0开始
(具体看题目给与的条件,注意审题)
3、特殊矩阵(可以压缩存储空间)
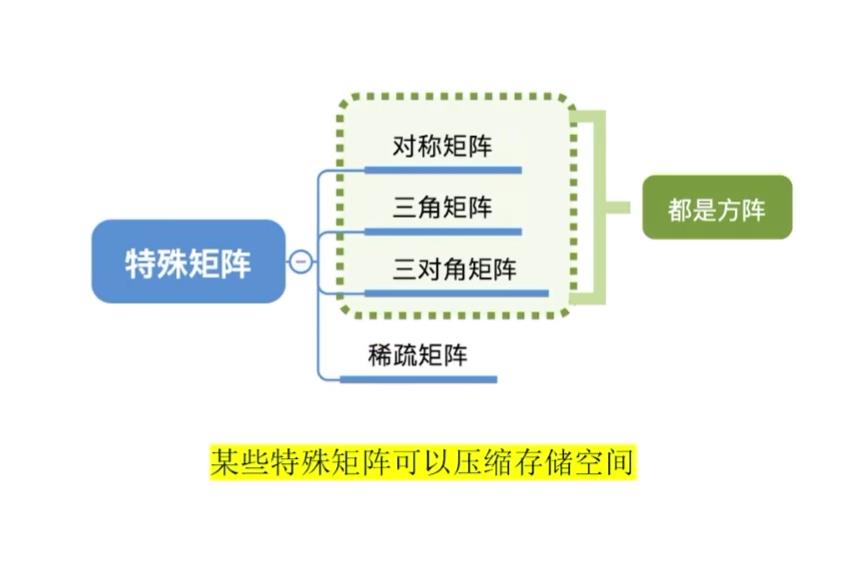
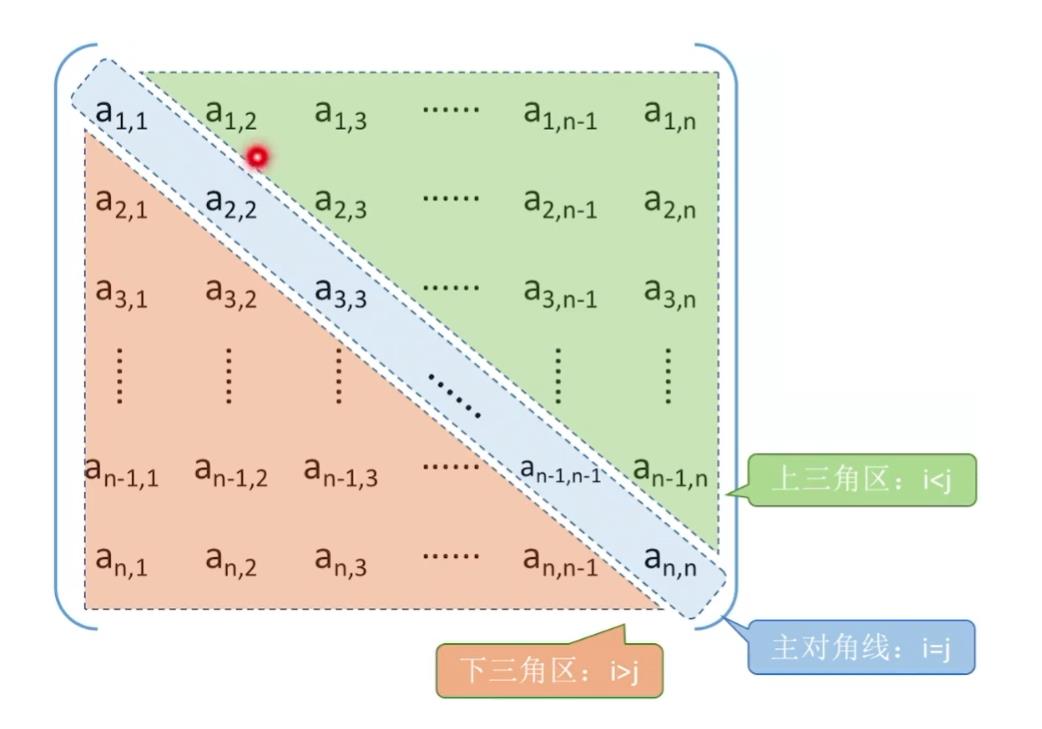
a、对称矩阵的压缩存储(方阵nxn即行数和列数是相同的)

压缩存储策略:只存储主对角线+下三角区(或主对角线+上三角区)
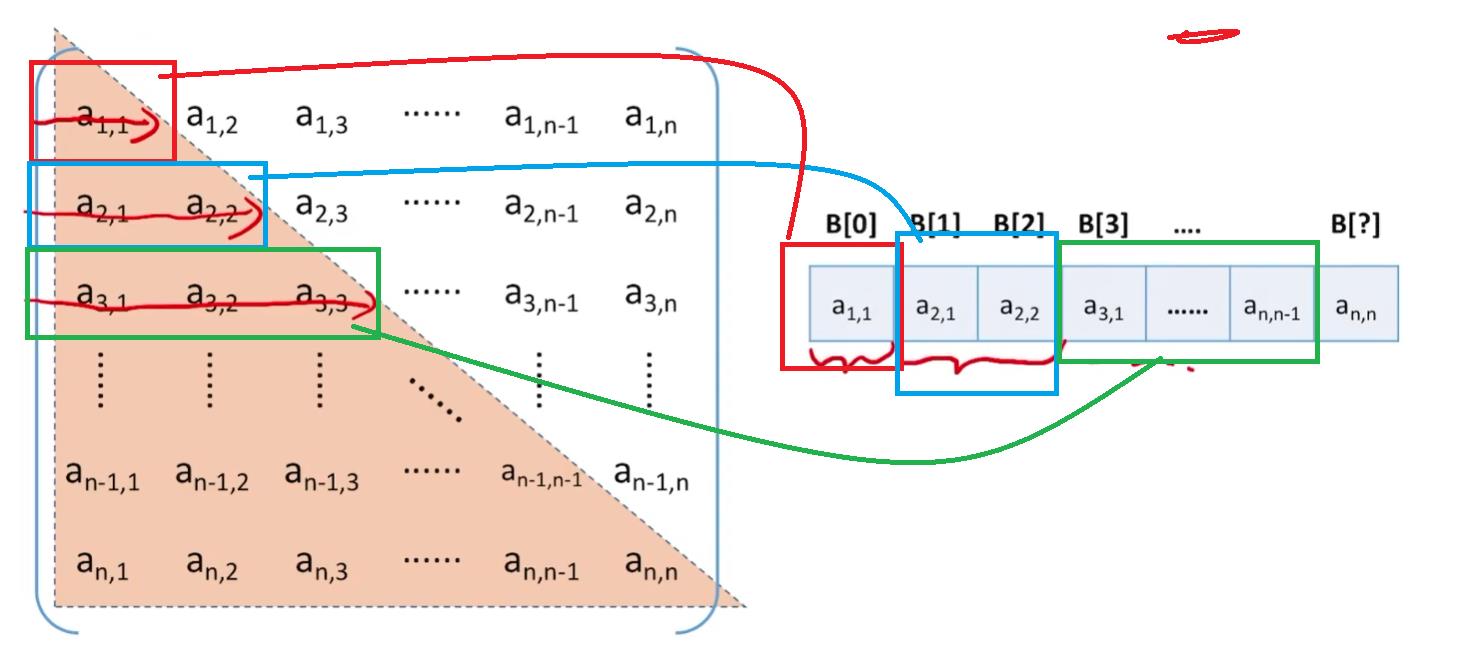
按照行优先原则存储将各个元素一次存入一维数组当中。
第一行
第二行
第三行
思考
数组大小应该是多少?
(1+n)* n/2
站在程序员的角度,对称矩阵压缩后怎样才能更加方便使用?
可以实现一个“映射”函数矩阵下标->一维数组下标
Key:按照行优先的原则,ai,j是第几个元素?

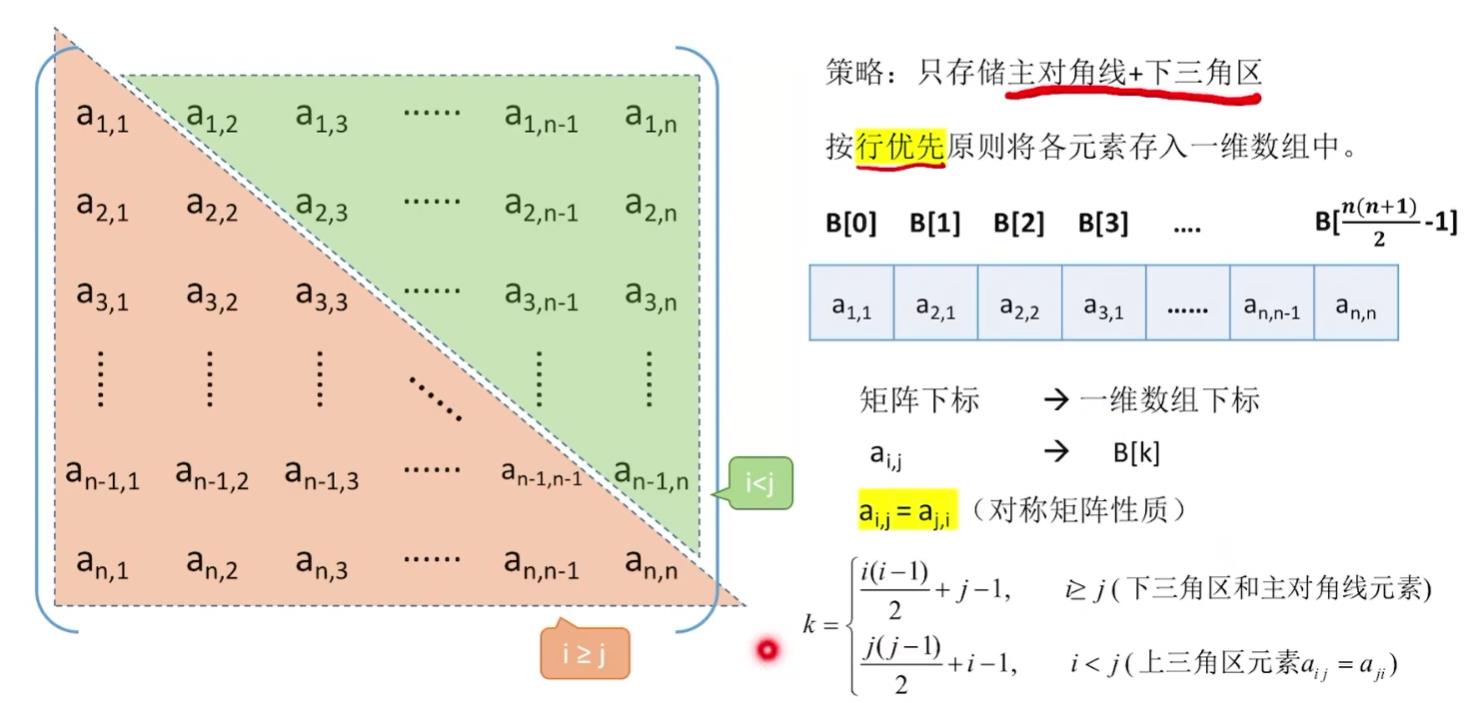
b、三角矩阵的压缩存储
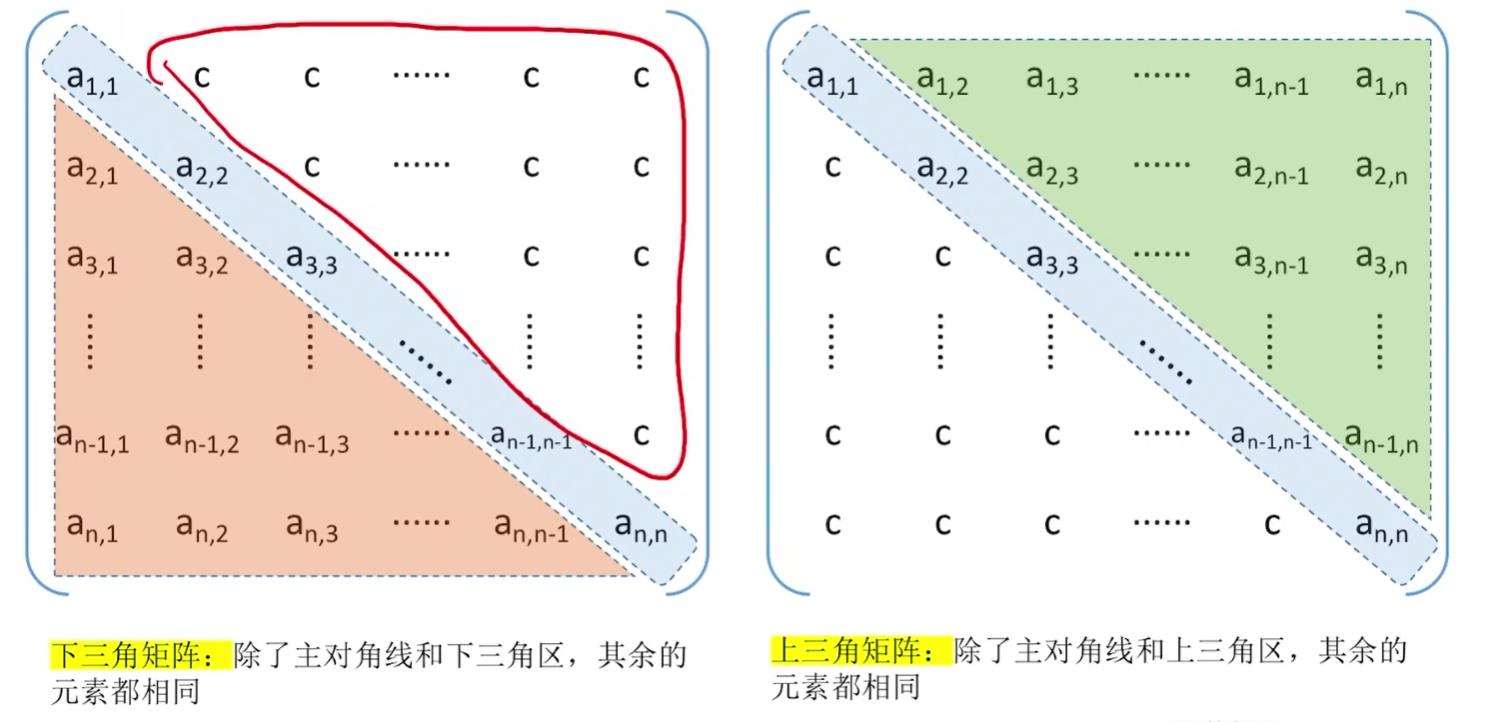

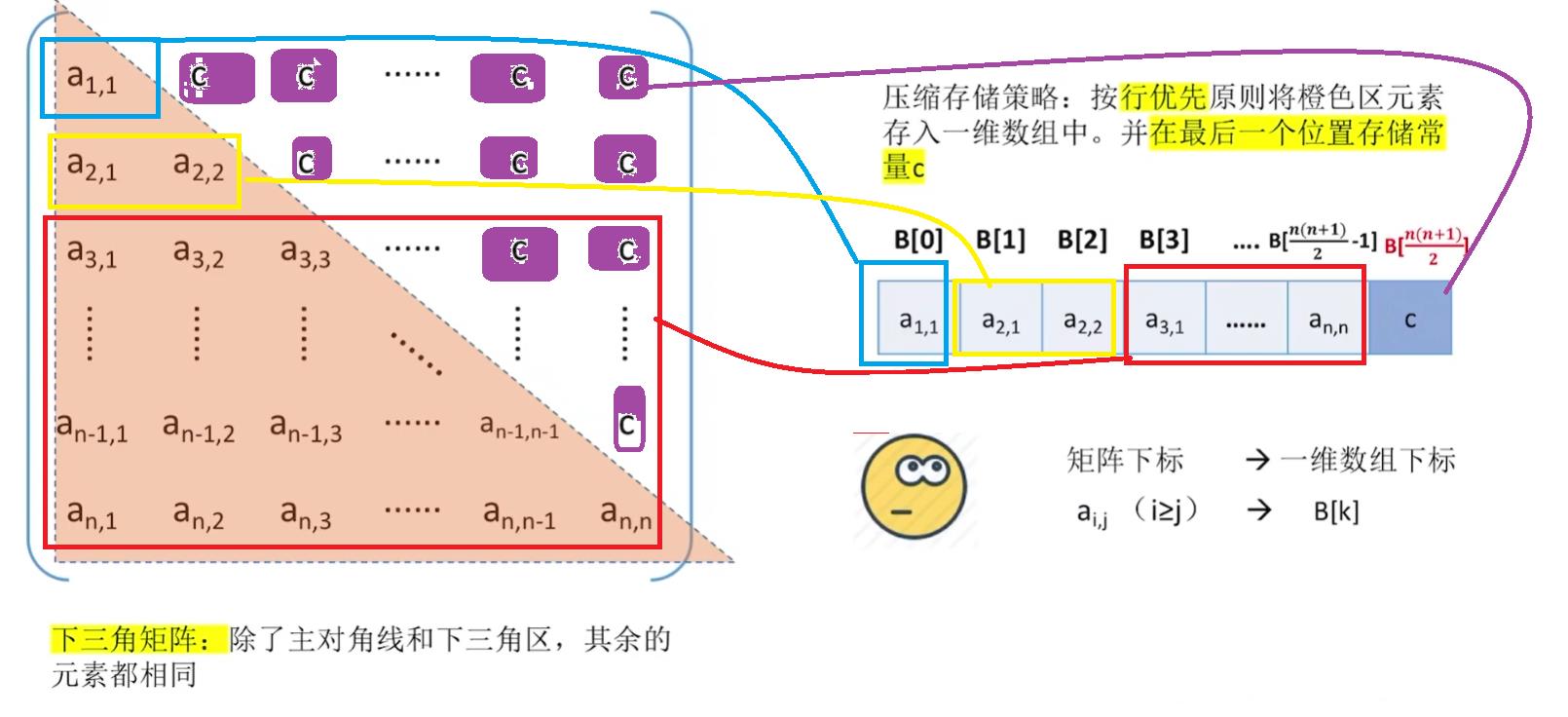

以上是关于C/C++语言数据结构快速入门(代码解析+内容解析)特殊矩阵的主要内容,如果未能解决你的问题,请参考以下文章
C/C++语言数据结构快速入门(代码解析+内容解析)栈的应用
C/C++语言数据结构快速入门(代码解析+内容解析)队列的应用