2021.8.9提高B组模拟1T4 着色（组合数学）

Posted 2021-09-04 SSL_LKJ

着色

题目大意

有个电子工程系的学生从小喜欢涂颜色。现在他买了本涂色书和K种不同的颜料开始涂色。有趣的是它并不喜欢色彩斑斓的图案，所以一幅图他最多只会用3种不同的颜料。还有，他不会把两个相邻区域涂成同样的颜色。当两个区域的边界至少有一个共同点时两个区域是相邻的。如下图，区域3和4是相邻的，区域1和2不是相邻的。下面的图给出了一种合法的涂色方案。

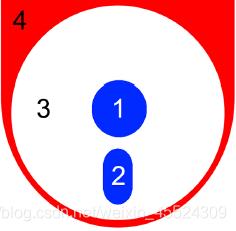
他想知道对于给定的一个图和颜料，有多少种合法的涂色方案。

输入样例

两个整数N（1<=N<=8），K（1<=K<=1000），N代表他要涂的是书里的第N张图片，K代表有K中不同的颜料选择。
这本书的内容请看后面！！

1.

2 2

2.

5 3

3.

7 3

输出样例

输出一个整数。代表合法的方案数。

1.

0

2.

12

3.

96

题目数据

N（1<=N<=8），K（1<=K<=1000）

题目提示

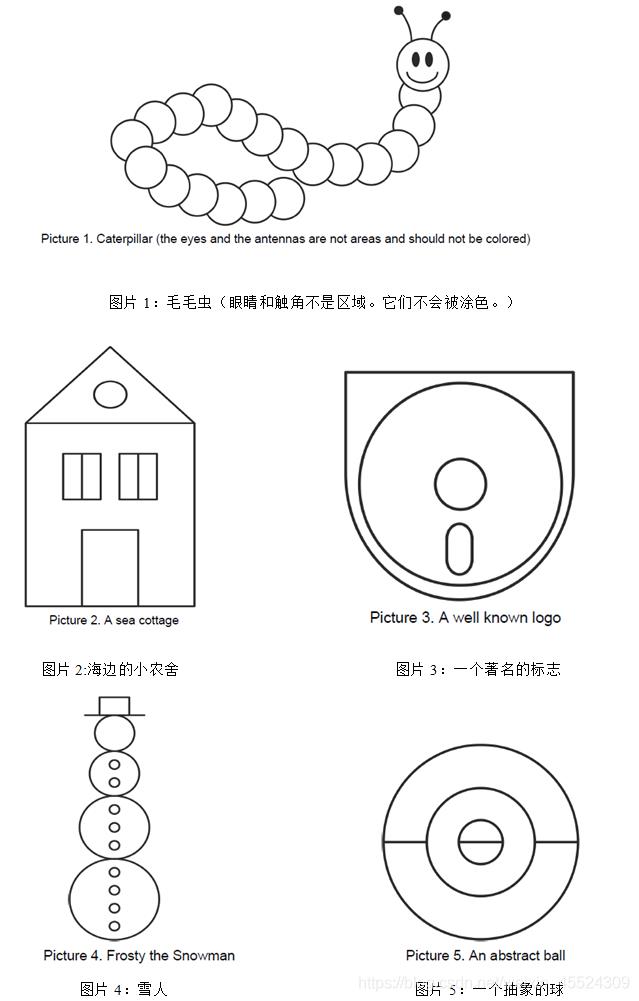
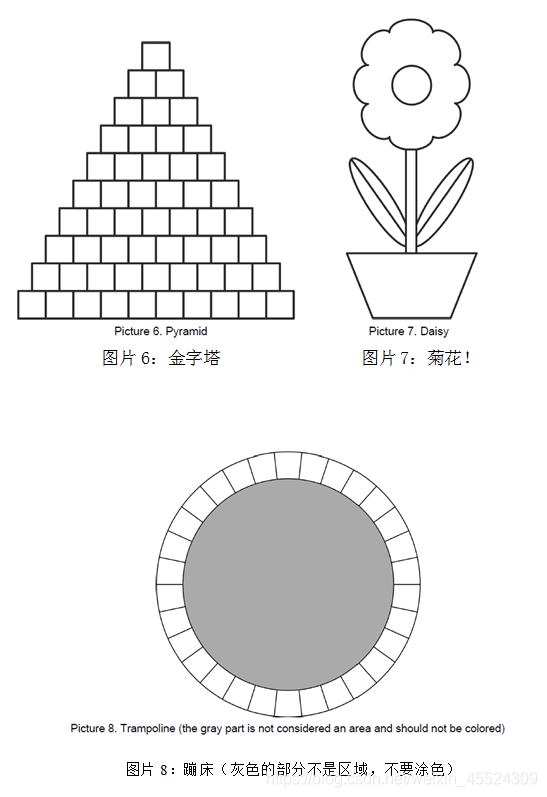
解题思路

每一个图每一个图去弄

得出规律求答案

可以先用组合数学求出 从k种颜色里选 $2和3$ 种颜色的方案数

例如第一个图

每两个颜色就有两种情况

每三个颜色的时候，就可以设头有三种情况，剩下的身体、尾巴就都只有两种情况，再相乘

三种情况最后的时候要-6

因为，假如有三个数，分别为 1  2  3

他不只是可以组成 1 2 3 2 1 2 3 ……

还可以 1 2 1 2 ……、 2 1 2 1 …… 、1 3 1 3 ……、 3 1 3 1 ……、2 3 2 3 ……、3 2 3 2 .

而这些是前面选两个颜色的时候求过的了

因此，要减去重复的6

AC代码

#include<cstdio>
using namespace std;
long long n,k;
int main()
{
	freopen("color.in","r",stdin);
	freopen("color.out","w",stdout);
	scanf("%lld%lld",&n,&k);
	long long C2=k*(k-1)/2,C3=k*(k-1)*(k-2)/6;  // 预处理
	
	if(n==1)printf("%lld",C2*2+C3*(3*(1<<19)-6));  // 每种情况分类讨论
		
	if(n==2)printf("%lld",C3*96);
		
	if(n==3)printf("%lld",C2*2+C3*18);
		
	if(n==4)printf("%lld",C2*2+C3*(3*(1<<13)-6));
		
	if(n==5)printf("%lld",C3*12);
		
	if(n==6)printf("%lld",C3*6);
		
	if(n==7)printf("%lld",C3*96);
		
	if(n==8)printf("%lld",C2*2+C3*1073741820);
			
	return 0;
}

谢谢