bellman_ford算法_有负权边的单源最短路问题

Posted 2021-09-04 一只特立独行的猫

当图中存在负权边时，dijkstra算法就不再适用，这是需要用到bellman_ford算法。算法思想是从每次连接所有的边，但是只更新到前一个结点的距离。如果不存在负权环，则在循环n次（结点数量）后一定可以得到答案。
伪码描述：

for i in n:
	for j in m:
		dis[边尾] = min(dis[边尾],back[边头]+边权)

题目：

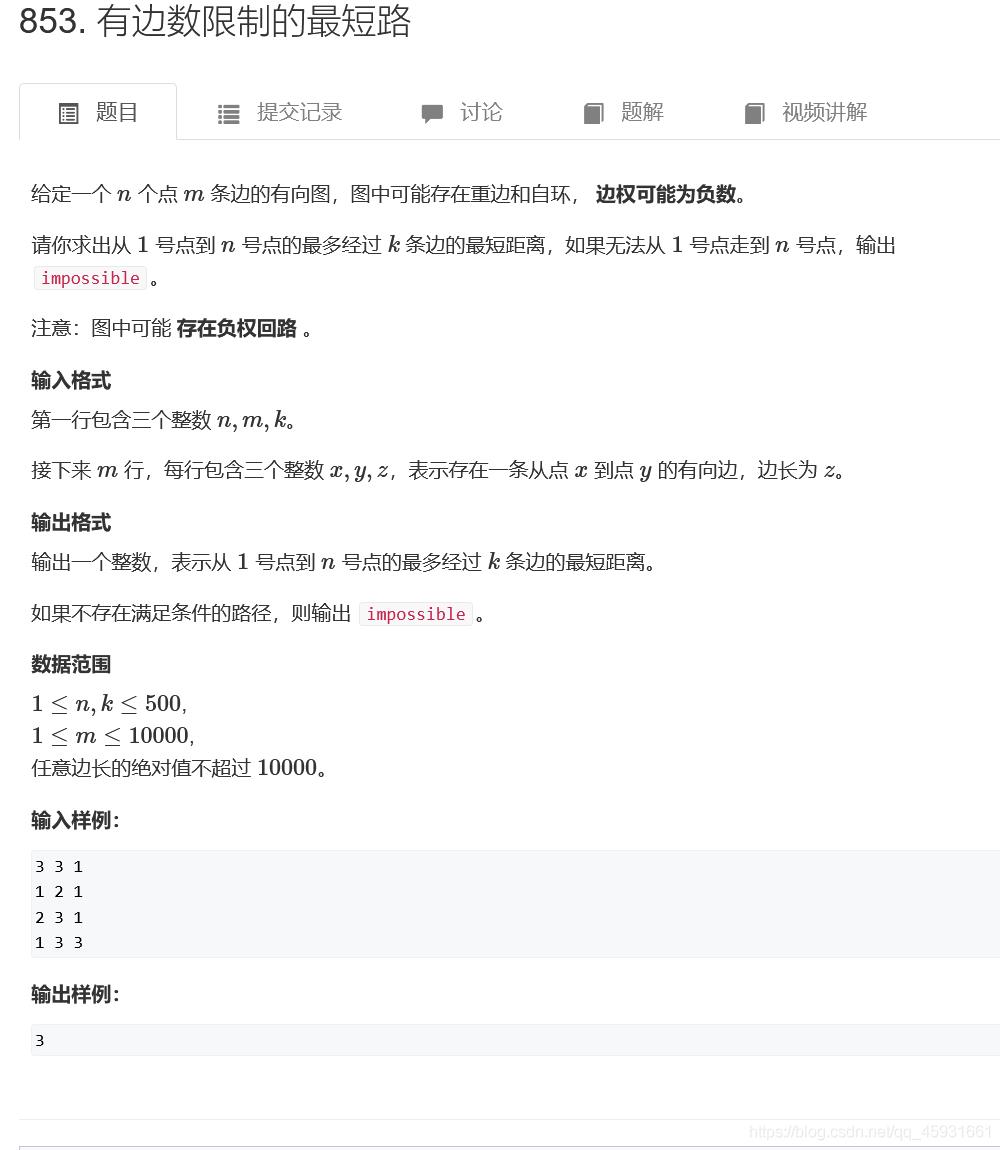
代码：

#include<iostream>
#include<cstring>

using namespace std;

const int N = 10005;

struct node {
	int a, b, w;
}edge[N];

int dis[505], backup[505];
int n, m, k;

int bellman_ford() {
	memset(dis, 0x3f, sizeof dis);
	//给定单源最短路的起点
	dis[1] = 0;
	for (int i = 0; i < k; i++) {
		//i表示从1出发，经过i条边的最短路
		memcpy(backup, dis, sizeof dis);
		for (int j = 0; j < m; j++) {
			int a, b, w;
			a = edge[j].a;
			b = edge[j].b;
			w = edge[j].w;
			dis[b] = min(dis[b], backup[a] + w);
		}
	}
	//除以2为了防止最大值在连边时减去数的问题
	if (dis[n] > 0x3f3f3f3f / 2) return -1;
	return dis[n];
}

int main() {
	cin >> n >> m >> k;
	for (int i = 0; i < m; i++) {
		int a, b, w;
		cin >> a >> b >> w;
		edge[i] = { a,b,w };
	}
	int k = bellman_ford();
	if (k == -1) {
		cout << "impossible" << endl;
	}
	else {
		cout << k << endl;
	}
	return 0;
}