Bellman_Ford和SPFA：带负边权的单源最短路算法

Posted 2021-08-02 清水寺扫地僧

文章目录

• • Bellman_Ford算法
  • SPFA算法

yxc的图最短路问题算法图镇楼：

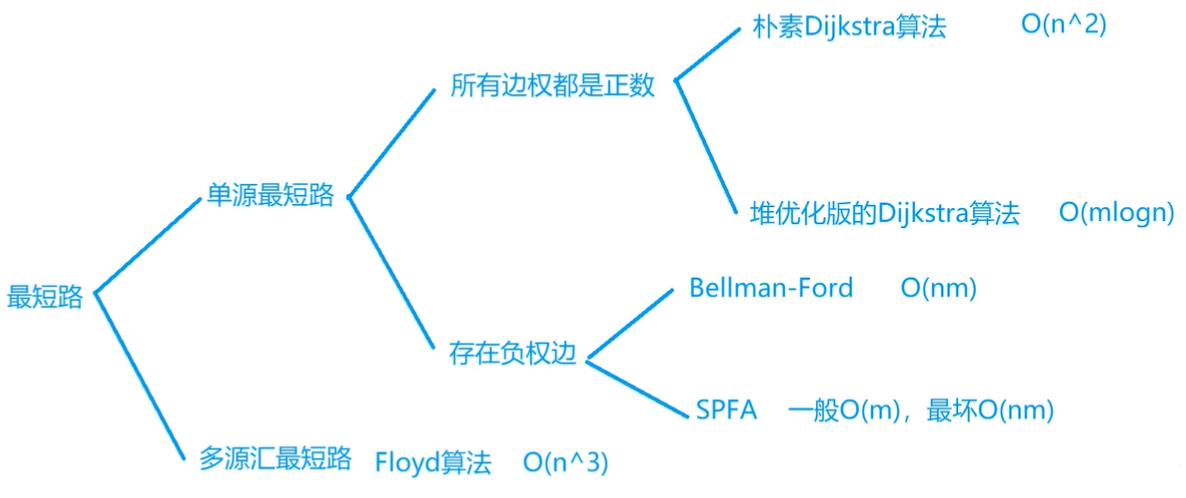
单源最短路所有边权为正：Dijkstra：正边权单源最短路算法；
单源最短路存在负权边：Bellman_Ford和SPFA：带负边权的单源最短路算法；
多源汇最短路：Floyd算法：多源汇最短路；

---

---

Bellman_Ford算法

• 初始化所有点到源点的距离为$\infty$,把源点到自己的距离设置为 $0$；
• 不管三七二十一遍历 $n$ 次;每次遍历 $m$ 条边，用每一条边去更新各点到源点的距离；
• 由以上的算法实现思路，可得出Bellman_Ford算法的时间复杂度为 $O(mn)$；

需要注意的点：

• 需要把dist数组进行一个备份backup，这样防止每次更新的时候出现串联；
• 由于存在负权边，因此return -1的条件就要改成dist[n]>0x3f3f3f3f >> 1;
• 上面所谓的 $n$ 次遍历的实际含义是当前的最短路径最多有 $n-1$ 条边，这也就解释了为啥要 $i$ 遍历到 $n$ 的时候退出循环了，因为只有 $n$ 个点,最短路径无环最多就存在 $n-1$ 条边（抽屉原理）。
• 这里无需对重边和自环做单独的处理：
  1）重边：由于遍历了所有的边，总会遍历到较短的那一条；
  2）自环: 有自环就有自环啊，反正又不会死循环;
• 该算法无非就是循环 $n$ 次然后遍历所有的边，因此不需要做什么特别的存储，只要把所有的边的信息存下来能够遍历就行；
• Bellman_Ford算法可以存在负权回路，因为它求得的最短路是有限制的，是限制了边数的，不会永久地走下去，会得到一个解；
• SPFA算法各方面优于该算法，但是碰到限制了最短路径上边的长度时就只能用Bellman_Ford了，此时直接把n重循环改成k次循环即可。

---

题目：853. 有边数限制的最短路
给定一个 $n$ 个点 $m$ 条边的有向图，图中可能存在重边和自环， 边权可能为负数。请你求出从 $1$ 号点到 $n$ 号点的最多经过 $k$ 条边的最短距离，如果无法从 $1$ 号点走到 $n$ 号点，输出 impossible。

注意：图中可能存在负权回路 。

输入格式
第一行包含三个整数 $n,m,k$。接下来 $m$ 行，每行包含三个整数 $x,y,z$，表示存在一条从点 $x$ 到点 $y$ 的有向边，边长为 $z$。

输出格式
输出一个整数，表示从 $1$ 号点到 $n$ 号点的最多经过 $k$ 条边的最短距离。如果不存在满足条件的路径，则输出 impossible。

数据范围
$1\le n,k\le 500,$
$1\le m\le 10000,$
任意边长的绝对值不超过 $10000$。

输入样例：

3 3 1
1 2 1
2 3 1
1 3 3

输出样例：

3

---

题目代码实现如下：

#include <iostream>
#include <cstring>

using namespace std;

const int N = 510, M = 10010;

struct Edge {
    int a;
    int b;
    int w;
} e[M]; //边数组，用来存储图中的边，a->b且权值为w
int dist[N]; //dist[i]记录节点1到节点i的距离，其中dist[1]=0
int backup[N]; //做备份，防止前面第1步进行边迭代后造成dist[i]的改变，导致一次步进实际上是两次的步进结果，具体情形见下面说明
int n, m, k; //k表示的是最短路径的长度

int bellman_ford() {
    memset(dist, 0x3f, sizeof(dist)); //将距离数组赋值为无限大
    dist[1] = 0; //将dist[1]赋值为0
    for(int i = 0; i < k; ++i) { //总共遍历k次，表明路径的长度为k
        memcpy(backup, dist, sizeof(dist)); //遍历边前进行dist的备份
        for(int j = 0; j < m; ++j) { //遍历所有的边
            int a = e[j].a, b = e[j].b, w = e[j].w;
            dist[b] = min(dist[b], backup[a] + w); //对点距离进行松弛操作，
            //使用backup:避免给a更新后立马更新b, 这样b一次性最短路径就多了两条边出来
        }
    }
    
    return dist[n];
}

int main() {
    scanf("%d%d%d", &n, &m, &k);
    for(int i = 0; i <= m; ++i) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        e[i] = {a, b, w};
    }
    int ret = bellman_ford();
    if(ret > 0x3f3f3f3f >> 1) puts("impossible");
    else cout << ret << endl;
    
    return 0;
}

注意：为什么需要backup[N]数组

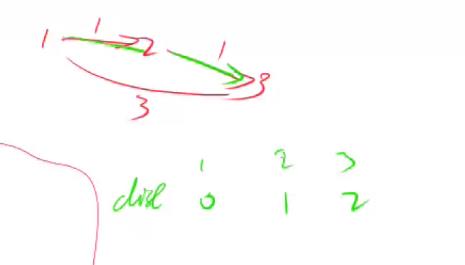
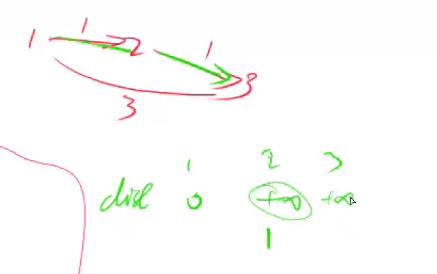
为了避免如左下的串联情况， 在边数限制为一条的情况下，节点3的距离应该是3，但是由于串联情况，利用本轮更新的节点2更新了节点3的距离，所以现在节点3的距离是2。造成了遍历一次，但是路径的长度(即路径通过点的个数)为 $2$，而不是 $1$，会造成错误。

正确做法是用上轮节点2更新的距离--无穷大，来更新节点3， 再取最小值，所以节点3离起点的距离是3。

造成串联的情况，当前边遍历过程更改了dist[i]中的数值

进行备份后，不再发生串联的情况

---

---

SPFA算法

SPFA算法是对Bellman_Ford算法的改进，在Bellman_Ford算法当中，我们注意到，Bellman_ford算法会遍历所有的边，但是有很多的边遍历了其实没有什么意义，我们只用遍历那些到源点距离变小的点所连接的边即可，只有当一个点的前驱结点更新了，该节点才会得到更新；因此考虑到这一点，我们将创建一个队列每一次加入距离被更新的结点。即值遍历需要进行松弛操作的，换句话说，每次遍历边时都是遍历的有效操作。

需要注意的点：

• st数组的作用：判断当前的点是否已经加入到队列当中了；已经加入队列的结点就不需要反复的把该点加入到队列中了，就算此次还是会更新到源点的距离，那只用更新一下数值而不用加入到队列当中。即便不使用st数组最终也没有什么关系，但是使用的好处在于可以提升效率。
• SPFA算法看上去和Dijstra算法长得有一些像但是其中的意义还是相差甚远的:
  （1）Dijkstra算法中的st数组保存的是当前确定了到源点距离最小的点，且一旦确定了最小那么就不可逆了(不可标记为true后改变为false)；SPFA算法中的st数组仅仅只是表示的当前发生过更新的点，且spfa中的st数组可逆(可以在标记为true之后又标记为false)。顺带一提的是BFS中的st数组记录的是当前已经被遍历过的点。
  （2） Dijkstra算法里使用的是优先队列保存的是当前未确定最小距离的点，目的是快速的取出当前到源点距离最小的点；SPFA算法中使用的是队列(你也可以使用别的数据结构),目的只是记录一下当前发生过更新的点。
• ⭐️Bellman_ford算法里最后return-1的判断条件写的是dist[n]>0x3f3f3f3f >> 1;而spfa算法写的是dist[n]==0x3f3f3f3f：
  其原因在于Bellman_ford算法会遍历所有的边，因此不管是不是和源点连通的边它都会得到更新；但是SPFA算法不一样，它相当于采用了BFS，因此遍历到的结点都是与源点连通的，因此如果你要求的n和源点不连通，它不会得到更新，还是保持的0x3f3f3f3f。
• ⭐️ Bellman_ford算法可以存在负权回路，是因为其循环的次数是有限制的因此最终不会发生死循环；但是SPFA算法不可以，由于用了队列来存储，只要发生了更新就会不断的入队，因此假如有负权回路请你不要用SPFA否则会死循环。
• ⭐️由于SPFA算法是由Bellman_ford算法优化而来，在最坏的情况下时间复杂度和它一样即时间复杂度为 $O(nm)$ ，假如题目时间允许可以直接用SPFA算法去解Dijkstra算法的题目。(好像SPFA有点小小万能的感觉?)
• ⭐️求负环一般使用SPFA算法，方法是用一个cnt数组记录每个点到源点的边数，一个点被更新一次就+1，一旦有点的边数达到了n那就证明存在了负环。

---

题目：851. spfa求最短路
给定一个 $n$ 个点 $m$ 条边的有向图，图中可能存在重边和自环， 边权可能为负数。请你求出 1 号点到 n 号点的最短距离，如果无法从 $1$ 号点走到 $n$ 号点，则输出 impossible。

数据保证不存在负权回路。

输入格式
第一行包含整数 $n$ 和 $m$。接下来 $m$ 行每行包含三个整数 $x,y,z$，表示存在一条从点 $x$ 到点 $y$ 的有向边，边长为 $z$。

输出格式
输出一个整数，表示 $1$ 号点到 $n$ 号点的最短距离。如果路径不存在，则输出 impossible。

数据范围
$1\le n,m\le 105,$
图中涉及边长绝对值均不超过 $10000$。

输入样例：

3 3
1 2 5
2 3 -3
1 3 4

输出样例：

2

---

题目代码实现如下：

#include <iostream>
#include <cstring>

using namespace std;

const int N = 100010;
int h[N], e[N], ne[N], w[N], idx;
int n, m;
int dist[N];
bool st[N]; //st[i]记录节点i当前是否在队列当中，即是否在等待进行新的松弛操作
int q[N], tt, hh;

void add(int a, int b, int c) {
    e[idx] = b;
    ne[idx] = h[a];
    w[idx] = c;
    h[a] = idx++;
}

//这里的代码和小根堆优化的Dijkstra算法有些类似，只不过优化的Dijkstra不可以不使用
//st[N]数组，这里可以，因为是为了记录节点是否在已经更新的队列当中，作为是否加入队列的依据
//加入st为了可以提高算法的运行效率，因为重复加入到队列当中并无多大意义
int spfa() {
    q[++tt] = 1;
    st[1] = true;
    
    while(hh <= tt) {
        int t = q[hh++];
        st[t] = false; 
        //从队列中取出来之后该节点st被标记为false,
        //代表之后该节点如果发生更新可再次入队
        for(int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            dist[j] = min(dist[j], dist[t] + w[i]);
            if(dist[j] == dist[t] + w[i] && !st[j]) {
            //当前已经加入队列的结点，无需再次加入队列，
            //即便发生了更新也只用更新数值即可，重复添加降低效率
                q[++tt] = j; st[j] = true;
            }
        }
    }
    
    return dist[n];
}

int main() {
    memset(h, -1, sizeof(h));
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    
    scanf("%d%d", &n, &m);
    for(int i = 0; i < m; ++i) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        add(a, b, w);
    }
    
    int ret = spfa();
    
    if(ret > 0x3f3f3f3f >> 1) puts("impossible");
    else printf("%d", ret);
    
    return 0;
}