下一代通信的野心:超奈奎斯特!超香农?
Posted 边缘计算社区
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了下一代通信的野心:超奈奎斯特!超香农?相关的知识,希望对你有一定的参考价值。
FTN,Faster-than-Nyquist,即超奈奎斯特,是一种可追溯到20世纪70年代的“古老的”、“新型”的传输技术。是什么让FTN历经半个世纪的发展依然历(争)久(议)弥(不)新(断),能在一波又一波的通信代际更迭中成为弄潮儿?下一代移动通信是谁家之天下,FTN厉兵秣马能否给出答案?由小编带你一探究竟。
先定个小目标,超他个奈奎斯特
要想解释什么是Faster-than-Nyquist,先得搞清楚什么是“Nyquist”——奈奎斯特第一准则。
在理想带限信道中(带宽为B),无码间干扰基带传输的最大符号速率为2B;要达到最高传输速率(奈奎斯特速率),必须使用带宽为B的理想低通滤波器进行滤波。


Harry Nyquist (1889-1976),1924年在“Certain Topics in Telegraph Transmission Theory”[1]上提出了无噪声信道下无码间干扰准则——奈奎斯特第一准则
这个……好像越解释越糊涂,梦回“通原”,瑟瑟发抖,还是举个例子吧。
有这么一串二进制序列——11010,经过2阶脉冲幅度调制进行基带传输。

理想低通滤波器又叫砖墙滤波器,它的冲击响应就是著名的“sinc”函数。这个函数的妙处在于从原点开始,相邻的两个零点之间是等间隔的。如果恰好后一个信号的sinc峰值对应前一个信号的零点,那么在采样时刻(注意!是采样时刻,不是处处!)就不存在码间干扰,这也可以看作是一种信号之间的“正交性”。这个“刚刚好”的发送间隔就是T=Tn=1/2B(这里把可以达到奈奎斯特速率的符号间隔设为Tn),可以达到奈奎斯特速率2B。

那么,要是发得更快一点行不行呢?试试以T=Tn/2=1/4B。虽然有望获得4B的速率,但是接收端在对应的采样时刻,就是一派“乱花渐欲迷人眼”的景象了,码间干扰严重,符号间的正交性被破坏。

看似码元速率是超了奈奎斯特了,但是带来了不可接受的码间干扰。难道“超奈奎斯特”传输就这?不,不,不,这么问,就格局小了!
1975年James Mazo发现,以二进制sinc脉冲发送信号,时间间隔为T=τTn,τ在[0.802,1]范围内,非正交性带来的码间干扰并不影响误码率性能(取决于符号之间的最小二乘欧式距离d2min)。在给定的调制方式下,可以多发送25%的比特——Mazo门限[2]。也就是说,当传输速率:
超过奈奎斯特门限时,脉冲信号开始失去正交性
进一步地,超过Mazo门限时,误码率开始下降
基于上述思想,FTN传输技术包含了对信号带宽、能量和误差性能的整体考量——信号的功率谱密度(PSD),提出了具有一定符号间干扰(以满足一定频谱形状)的非正交传输方案。FTN频谱效率提升的代价就是需要更为复杂的检测方法来缓解符号间的干扰问题。
各路英豪勃勃野心,香农容量岌岌可危?
FTN传输通过在单天线上进行多重数据流的移位重叠,可以实现媲美MIMO的传输效果。这“惊为天人”的技术引无数英雄竞折腰,各种衍生技术纷纷崛起,江湖上高举“OvXDM”[4]、“SE-FDM”[5]和“虚拟MIMO”[6]旗帜的各路英豪齐聚6G,风光无量。“FTN可以超越香农容量限”、“FTN可以用单天线实现多路独立并行传输”的观点一时间也甚嚣尘上。


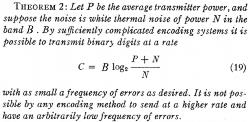
Claude Elwood Shannon (1916-2001),1949年发表“Communication in the Presence of Noise”[7],基于Harry Nyquist的研究成果,从随机过程的角度,提出了白噪声条件下的系统可达的最大传输速率——信道容量
香农容量界一直以来是通信人孜孜以求的目标,一直被逼近,从未被超越。故而,FTN传输技术备受争议。
超?还是不超?这是个问题。
要想回答这个问题必须清楚“FTN超经典香农容量”有哪些前提假设?这样的比较是否公平合理?上面提到的经典香农容量的证明是基于sinc脉冲波形的。而FTN整体考虑带宽、能量和误码率性能,采用非正交波形进行传输,而且由于sinc滤波器过于理想,并不能应用于实际系统中。所以为了进行公平合理的比较,需要对香农容量公式进行修订,引入PSD的影响,即

其中,|H(f)|2为频谱分布。利用该公式可以得到以下结论:当使用sinc脉冲时,FTN的容量与经典香农容量相等;当使用非sinc脉冲时,FTN的容量大于经典香农容量。
但是,当对实际带宽归一化后(即频谱效率),会发现:随着信噪比的提升,FTN的频谱效率与经典香农频谱效率渐进相等,即频谱效率并没有超越香农限
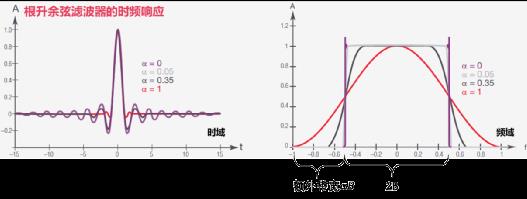
那么,FTN增加的容量来自于哪里呢?以实际常用的非sinc滤波器——根升余弦滤波器(时频响应见下图)为例,α为滚降系数,该值越大,意味着超出的额外带宽越大,FTN系统容量越高(见仿真图)。而FTN的高效传输正是利用了这部分带宽。
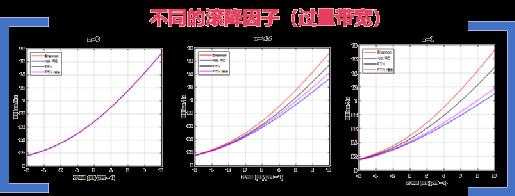
超不超的问题解决了,FTN真的可以用单天线实现多天线的独立并行传输吗?
还记得之前举的例子中FTN带来的码间干扰吗?那是在无噪声的情况下。对于一般的加性高斯白噪声的信道,噪声在接收端的各个采样点上的“码间干扰”就是噪声采样点之间有了相关性。并行可以,但是不独立!这就导致FTN并不能像MIMO那样实现频谱效率的成倍提升?

“5”里看花,群雄逐“6”
FTN的容量增益是靠额外的带宽换来的,虽然没有超过香农限,但依然对未来通信技术的发展提供了非常有益的新思路。
FTN是一种在高信噪比下逼近香农界的可行解决方案,其实质是以复杂度为代价换取频谱效率的提升。
FTN为滤波器的设计提供了新思路。传统滤波器以无码间干扰为设计目标,既然FTN允许存在码间干扰,可以按照频谱框架设计发送脉冲,充分利用频谱资源。
FTN能否在下一代通信技术中大展拳脚,还有很多实际问题需要解决:
低复杂度接收机的设计对该系统的实用化发展至关重要。
FTN如何与OFDM、MIMO、编码技术相融合有待进一步研究。
立足5G,展望6G,通信场上风云际会,雄关漫道真如铁,而今迈步从头越。
参考文献
[1] Nyquist, H. (1928). Certain Topics in Telegraph Transmission Theory. Transactions of the American Institute of Electrical Engineers, 47(2), 617-644. doi:10.1109/T-AIEE.1928.5055024
[2] Mazo, J.E. (1975), Faster-Than-Nyquist Signaling. Bell System Technical Journal, 54: 1451-1462. https://doi.org/10.1002/j.1538-7305.1975.tb02043.x
[3] Liveris, A. D., & Georghiades, C. N. (2003). Exploiting faster-than-Nyquist signaling. IEEE Transactions on Communications, 51(9), 1502-1511. doi:10.1109/TCOMM.2003.816943
[4] 李道本. (2016). 重叠复用原理下加性白高斯噪声信道的容量. 北京邮电大学学报, 39(006), 1-10.
[5] Darwazeh, I. , Xu, T. , Gui, T. , Bao, Y. , & Li, Z. . (2014). Optical sefdm system; bandwidth saving using non-orthogonal sub-carriers. IEEE Photonics Technology Letters, 26(4), 352-355.
[6] Wang, Q. , Chang, Y. , & Yang, D. . (2007). Deliberately designed asynchronous transmission scheme for mimo systems. IEEE Signal Processing Letters, 14(12), 920-923.
[7] Shannon, C. E. (1998). Communication In The Presence Of Noise. Proceedings of the IEEE, 86(2), 447-457. doi:10.1109/JPROC.1998.659497
作者 | 中国移动研究院 :苏鑫、金婧、王森、王启星、赵殊伦、楼梦婷
感谢阅读,欢迎扩散传播!感谢!
边缘计算社区:促进边缘计算领域知识传播,中立,客观,如果您关注边缘计算、5G、物联网、云原生等领域请关注我们。

以上是关于下一代通信的野心:超奈奎斯特!超香农?的主要内容,如果未能解决你的问题,请参考以下文章
计算机网络学习笔记——物理层奈奎斯特/香农定理物理接口传输介质交换电信网络无线网络