❤️死磕排序系列之 「 选择排序 」 ❤️ (建议排序)

Posted 2021-08-29 英雄哪里出来

• 本文已收录于专栏《数据结构入门》

文章目录

• 零、📃前言
• 一、🎯简单释义
• 二、🧡核心思想
• 三、🔆动图演示
• 四、🌳算法前置
• 五、🥦算法描述
• 六、🧶算法分析
• 七、🧢优化方案
• 八、💙源码详解
• 九、💗代码验证

零、📃前言

  这个系列的文章中，我会着重讲解一些常见的 「算法和数据结构」 的设计思想，并且配上动图。希望读者能够带上自己的 「思考」，主要针对面试中常见的问题和新手朋友们比较难理解的点进行解析。当然，这个系列的文章，后面也会给出面向算法竞赛的提纲，如果有兴趣深入学习的欢迎在「评论区留言，一起成长交流」 。
  零基础学算法的最好方法，莫过于刷题了。当然，刷题是不够的，刷的过程中也要多多总结，多多思考，养成 「经常思考」 的习惯，这就是所谓的 「 流水不腐，户枢不蠹 」，任何事情都是需要坚持的，刷题也一样，没有刷够足够的题，就很难做出系统性的总结。所以上大学的时候，我花了三年的时间来刷题， 工作以后还是会抽点时间出来刷题。
  千万不要用工作忙来找借口，时间挤一挤总是有的。当然，每天不需要花太多时间在这个上面，把这个事情做成一个规划，按照长期去推进。反正也没有 KPI 压力，就当成是工作之余的一种消遣，还能够提升思维能力。
  所以，无论你是 小学生，中学生，高中OIer，大学ACMer，职场人士，只要想开始，一切都不会太晚！
  今天要讲的主要内容是：「 选择排序 」，希望读者朋友给个面子，帮我完成阅读，不能完读，我可就完犊子了 🤣，当然，如果你觉得还可以，给我个「 赞 」 和 「 收藏 」，这个对我很重要，谢谢了！

  「 选择排序 」 是比较直观且编码简单的排序算法，虽然效率不是很高，但一般也出现在各种 「数据结构」 的教科书上。于是，我来了。我会尽量做到「深入浅出」，让 90% 的 「零基础小白 」 也都能理解，真正做到 「让天下没有难学的算法」 。我知道这很难，但是我愿意尝试！我会尽量把文章写得有趣。

🙉饭不食，水不饮，题必须刷🙉
C语言免费动漫教程，和我一起打卡！ 🌞《光天化日学C语言》🌞
LeetCode 太难？先看简单题！ 🧡《C语言入门100例》🧡
数据结构难？不存在的！ 🌳《数据结构入门》🌳
LeetCode 太简单？算法学起来！ 🌌《夜深人静写算法》🌌
究极算法奥义！深度学习！ 🟣《深度学习100例》🟣

那么，我的教程和别人的教程有什么不同的地方呢？
  「第一步」简单释义： 我会简单解释一下这个算法的目的、思想、以及为什么叫这个名字以帮助记忆。
  「第二步」核心思想： 我会大致介绍一下这个算法的核心思想。
  「第三步」动图演示： 我会引入一个动图，并且用一个切实的例子展示一下算法执行的全过程。
  「第四步」算法前置： 在学习这个算法之前，我们需要学习的前置内容有哪些？这些内容是需要事先去攻克的。
  「第五步」算法描述： 细致的讲解整个算法的执行流程。
  「第六步」算法分析： 对算法的时间复杂度和空间复杂度进行一个详细的分析。
  「第七步」优化方案： 介绍一些可以优化的点。
  「第八步」代码实践： 用 C/C++ 来实现上述算法。
  「第九步」代码验证： 最后，我会推荐一些比较好用的在线评测系统来验证我们实现的算法的正确性。

一、🎯简单释义

1、算法目的

  将原本乱序的数组变成有序，可以是 「升序」 或者 「降序」 （为了描述统一，本文一律只讨论 「 升序」 的情况）。

2、算法思想

  通过不断从未排序的元素中，「比较」 和 「交换」，从而 「选择」 出一个最小的， 直到最后变成一个「升序」 序列，则算法结束。

3、命名由来

  每次都是「选择」 出一个最小的元素，故此命名 「 选择排序 」 。

二、🧡核心思想

• 「迭代」：类似的事情，不停地做。
• 「比较」：关系运算符 小于($<$) 的运用。
• 「交换」：变量或者对象的值的互换。

三、🔆动图演示

1、样例

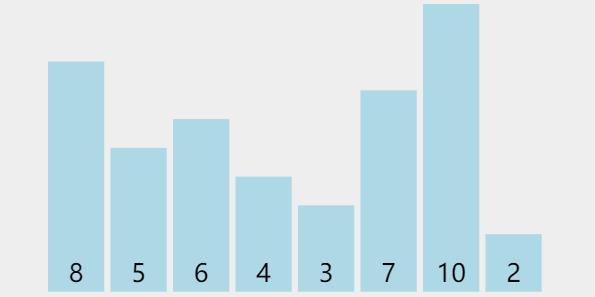
8	5	6	4	3	7	10	2

• 初始情况下的数据如 图二-1-1 所示，基本属于乱序，纯随机出来的数据。

图二-1-1

2、算法演示

• 接下来，我们来看下排序过程的动画演示。如 图二-2-1 所示：

图二-2-1

3、样例说明

图示	含义
■ 的柱形	代表尚未排好序的数
■ 的柱形	代表正在执行 比较 的数
■ 的柱形	代表已经排好序的数
■ 的柱形	有两种：1、记录最小元素 2、执行交换的元素

  我们发现，首先从 「第一个元素」 到 「最后一个元素」 中选择出一个 「最小的元素」，和 「第一个元素」 进行 「交换」；
  然后，从 「第二个元素」 到 「最后一个元素」 中选择出一个 「最小的元素」，和 「第二个元素」 进行 「交换」。
  最后，一定可以保证所有元素都是 「升序」 排列的。

四、🌳算法前置

1、循环的实现

• 这个算法本身需要做一些「 循环 」进行迭代计算，所以你至少需要知道「 循环 」 的含义，这里以 「 c++ 」 为例，来看下一个简单的「 循环 」是怎么写的。代码如下：

int n = 5201314;
for(int i = 0; i < n; ++i) {
    // TODO ： 。。。
}

• 这个语句就是一个最简单的循环语句，它会将循环体内的语句执行 $n$ 次，而这里的 $n$ 等于 $5201314$，也就是会执行 $5201314$ 次。

2、比较的实现

• 「比较」两个元素的大小，可以采用关系运算符，本文我们需要排序的数组是按照 「升序」 排列的，所以用到的关系运算符是 「小于运算符（即 <）」 。
• 我们可以将两个数的「比较」写成一个函数smallerThan，以 「 c++ 」 为例，实现如下：

#define Type int
bool smallerThan(Type a, Type b) {
    return a < b;
}

• 其中Type代表数组元素的类型，可以是整数，也可以是浮点数，也可以是一个类的实例，这里我们统一用int来讲解，即 32位有符号整型。

3、交换的实现

• 所谓「交换」，就是对于两个变量，将它们的值进行互换。
• 在 「Python」 中，我们可以直接写出下面这样的代码就实现了变量的交换。

a, b = b, a

• 在 「 c++ 」 里，这个语法是错误的。
• 我们可以这么理解，你有两个杯子 $a$ 和 $b$，两个杯子里都盛满了水，现在想把两个杯子里的水「交换」一下，那么第一个想到的方法是什么？

当然是再找来一个临时杯子：
  1）先把 $a$ 杯子的水倒进这个临时的杯子里；
  2）再把 $b$ 杯子的水倒进 $a$ 杯子里；
  3）最后把临时杯子里的水倒进 $b$ 杯子；

• 这种就是临时变量法。以 「 c++ 」 为例，实现如下：

#define Type int
void swap(Type* a, Type* b) {
    Type tmp = *a;     // 把 a 杯子的水倒进临时杯子
    *a = *b;           // 把 b 杯子的水倒进 a 杯子
    *b = tmp;          // 把 临时杯子 的水 倒进 b 杯子
}

• 这里*涉及到的「指针」相关知识，属于语法层面，请自行学习。

五、🥦算法描述

1、问题描述

  给定一个 $n$ 个元素的数组，数组下标从 $0$ 开始，采用「 选择排序 」将数组按照 「升序」排列。

2、算法过程

整个算法的执行过程分以下几步：
  1） 循环迭代变量 $i=0\to n-1$；
  2） 每次迭代，令 $min=i$，$j=i+1$；
  3） 循环执行比较 $a[j]$ 和 $a[min]$，如果产生 $a[j]<a[min]$ 则执行 $min=j$。执行 $j=j+1$，继续执行这一步，直到 $j==n$；
  4） 交换 $a[i]$ 和 $a[min]$，回到 1）。

六、🧶算法分析

1、时间复杂度

• 我们假设 「比较」 和 「交换」 的时间复杂度为 $O(1)$。
• 「 选择排序 」 中有两个嵌套循环。

外循环正好运行 $n-1$ 次迭代。 但内部循环运行变得越来越短：
  当 $i=0$，内层循环 $n-1$ 次「比较」操作。
  当 $i=1$，内层循环 $n-2$ 次「比较」操作。
  当 $i=2$，内层循环 $n-3$ 次「比较」操作。
  ……
  当 $i=n-3$，内层循环 $2$ 次「比较」操作。
  当 $i=n-2$，内层循环 $1$ 次「比较」操作。

• 因此，总「比较」次数如下：
• $$(n-1)+...+2+1=\frac{n(n-1)}{2}$$
• 总的时间复杂度为：$O(n^2)$

2、空间复杂度

• 由于算法在执行过程中，只有「选择最小元素」的时候，需要事先将最小元素的下标存入临时变量min，而其它没有采用任何的额外空间，所以空间复杂度为 $O(1)$。

七、🧢优化方案

  「 选择排序 」在众多排序算法中效率较低，时间复杂度为 $O(n^2)$ 。
   想象一下，当有 $n=10^5$ 个数字。 即使我们的计算机速度超快，并且可以在 1 秒内计算 $10^8$ 次操作，但冒泡排序仍需要大约一百秒才能完成。
  考虑一下，每一个内层循环是从一个区间中找到一个最小值，并且更新这个最小值。是一个「 动态区间最值 」问题，所以这一步，我们是可以通过「 线段树 」 来优化的。这样就能将内层循环的时间复杂度优化成 $O(lo{g}_{2}n)$ 了，总的时间复杂度就变成了 $O(nlo{g}_{2}n)$。
  由于「 线段树 」不是本文讨论的重点，有兴趣了解「 线段树 」相关内容的读者，可以参考以下这篇文章：夜深人静写算法（三十九）- 线段树。

八、💙源码详解

#include <stdio.h>

int a[1010];

void input(int n, int *a) {
    for(int i = 0; i < n; ++i) {
        scanf("%d", &a[i]);
    }
}

void output(int n, int *a) {
    for(int i = 0; i < n; ++i) {
        if(i)
            printf(" ");
        printf("%d", a[i]);
    }
    puts("");
}

void swap(int *a, int *b) {
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

void SelectionSort(int n, int *a) {  // (1)
    int i, j;
    for(i = 0; i < n - 1; ++i) {     // (2)
        int min = i;                 // (3)
        for(j = i+1; j < n; ++j) {   // (4)
            if(a[j] < a[min]) {
                min = j;             // (5)
            }
        }
        swap(&a[i], &a[min]);        // (6) 
    }
}

int main() {
    int n;
    while(scanf("%d", &n) != EOF) {
        input(n, a);
        SelectionSort(n, a);
        以上是关于❤️死磕排序系列之 「 选择排序 」 ❤️ (建议排序)的主要内容，如果未能解决你的问题，请参考以下文章
 
 ❤️五万字《十大排序算法》动图讲解❤️(建议收藏)
 Python数据结构系列☀️《查找排序-基础知识》——知识点讲解+代码实现☀️
 ❤️数据结构入门❤️（4 - 2）- 选择排序
 万字整理❤️8大排序算法❤️建议收藏
 JavaScript之算法设计思想
 ❤️「 选择排序 」❤️