void bubbleSort(int g[], int n) {
    bool flag = true; //检查数组是否有序
    for(int i = 0;i < n-1; ++i){
        flag = false;
        for(int j = 0; j < n-i-1; ++j){//n-i-1 已经有序的元素不再比较
            if(g[j] > g[j+1]){
                swap(g[j], g[j+1]);
                flag = true;
            }
        }
        if(!flag) break; // flag = false 表示没有交换元素，数组已经有序
    }
}

4. 算法复杂度

空间复杂度：除了本身的数组不需要额外的存储空间，故空间复杂度为 O(1)。

时间复杂度：有两层 for 循环，排序次数的时间复杂度为 O(n)，交换次数的时间复杂度为O(n)，因为是嵌套的，故总的复杂度为O(n^2)。

二、选择排序

1. 算法思想

选择排序是一个比较简单的排序，是一种基于选择的排序算法，但并不是一个稳定的排序算法。

基本思想（从小到大排序）：选择数组最小的元素，与数组第一个元素交换，然后选择剩余的数组元素中最小的元素，与数组第二个元素交换，一直重复上述操作，直到数组有序。

2. 实例演示

下面以数组 [7, 9, 5 , 3, 1] 为例进行从小到大排序的演示：

第一趟排序：

遍历一遍数组，最小的元素是1，与第一个元素 7 交换。

第一趟排序的结果为：

[1, 9, 5, 3, 7]

第一趟排序后，元素 1 已经在最终排序位置上。

第二趟排序：

遍历一遍数组剩余元素，最小元素是3，3 与 9 交换。

第二趟排序的结果为：

[1, 3, 5, 9, 7]

经过第三趟排序后，将 3 放置到最终排序位置（其实 5 也已经在最终位置了）

第三趟排序：

遍历一遍数组剩余元素，最小元素是 5，已经在最终排序位置，不用交换。

第三趟排序的结果为：

[1, 3, 5, 9, 7]

第四趟排序：

遍历一遍数组剩余元素，最小元素是 7，将 7 与 9 交换。

第四趟排序结果为：

[1, 3, 5, 7, 9]

第四趟排序后，全部元素已经有序。

3. 代码实现

void selectSort(int a[], int n){
    int Min;
    for(int i = 0;i < n-1; ++i){//选择 n-1 次
        Min = i;
        for(int j = i+1; j < n; ++j){//从 i-n之间选择一个最小值放在i处。
            if(a[j] < a[Min]){
                Min = j;
            }
        }
        if(Min != i){
            swap(a[i], a[Min]);
        }
    }
}

4. 算法复杂度

空间复杂度：除了本身的数组不需要额外的存储空间，故空间复杂度为 O(1)。

时间复杂度：两层嵌套的 for 循环，每个的时间复杂度为O(n)，故总的时间复杂度为O(n^2)

三、快速排序

1. 算法思想

快速排序是一种更优的排序算法，是一种不稳定的排序算法。它采用分而治之的思想，每次排序选择待排序序列的一个值，该值作为枢纽值，以该值为基点，小于该值的交换到左边，大于该值的交换到右边。然后，重复上述操作，排序左右两边待排序的序列。一直分解到单个元素，每次分解都会确定一个元素的最终位置。

那么，交换的规则是什么呢？

以左边第一个是枢纽值为例，枢纽值首先从右向左找到一个小于枢纽值的元素，将这个元素与枢纽值交换位置，交换后再从左到右与枢纽值进行比较，找到一个比枢纽值大的元素，与枢纽值交换，然后重复上述过程，直到枢纽值左边元素不大于枢纽值，枢纽值右边不小于枢纽值为止。

2. 实例演示

下面以数组 [5, 7, 9 , 3, 1] 为例进行从小到大排序的演示：

枢纽值的选择以待排序序列的第一个为例。

首先，选取 5 为枢纽值，先从右向左找到一个小于枢纽值 5 的值，并与之交换位置，很明显，

5 与 1 交换，交换后数组变为：

[1, 7, 9, 3, 5]

然后，从左向右找到一个比枢纽值大的元素，并与之交换位置，这个元素是7，与5交换位置后，数组变为：

[1, 5, 9, 3, 7]

然后，从右向左找到一个比枢纽值小的元素，并与之交换位置，这个元素是3，与5交换位置后，数组变为：

[1, 3, 9, 5, 7]

然后，从左向右找到一个比枢纽值大的元素，并与之交换位置，这个元素是 9，与5交换位置后，数组变为：

[1, 3, 5, 9, 7]

然后重复上述操作，排序[1, 3] 和 [9, 7]两个序列。

序列[1, 3]， 1为枢纽值，从右向左找到一个比枢纽值1 小的元素，序列已经有序了，1 的右边值比1大，左边没有值。因为1右边序列[3] 只有一个元素，故不用排序。

序列[9, 7]，9 为枢纽值，从右向左找到一个比枢纽值9小的元素，这个元素是 7,7与9交换位置，交换后为：

[7, 9]，序列已经有序，枢纽值左边序列[7] 只有一个元素，故不用排序。

最后，得到有序序列 [1, 3, 5, 7, 9]。

3. 代码实现

递归版本：

/*快速排序算法
 * l ----- 序列左边下标
 * t ----- 序列右边下标
 * a[] --- 排序数组
 */
int Partition(int a[], int l, int t){//使用枢纽值划分待排序序列
    int idx = l + rand()%(t - l + 1);//枢纽值是随机选取的
    swap(a[l], a[idx]);
    int i = l;
    int j = t;
    int x = a[i];
    while(i < j){
        while(i < j && a[j] > x)
            j--;
        if(i < j)
            a[i++] = a[j];
        while(i < j && a[i] < x)
            i++;
        if(i < j)
            a[j--] = a[i];
    }
    a[i] = x;
    return i;
}
//递归进行划分
void Quick_Sort(int a[], int l, int t){
    if(l < t){
        int mid = Partition(a, l, t);//划分，返回基准值下标
        Quick_Sort(a, l, mid-1);//枢纽值左边待排序序列
        Quick_Sort(a, mid+1, t);//枢纽值右边待排序序列
    }
}

非递归版本：

//Pair存储待排序序列的第一个和最后一个坐标，
//这样就可以确定一个序列。
typedef pair<int, int> Pair;
int Partition(int a[], int lt, int rt){//以枢纽值划分待排序序列
    int i = lt;
    int j = rt;
    int rm = i + rand()%(j - i + 1);//枢纽值随机选取
    swap(a[i], a[rm]);
    int x = a[i];
    while(i < j){
        while(i < j && a[j] > x)
            j--;
        if(i < j)
            a[i++] = a[j];
        while(i < j && a[i] < x)
            i++;
        if(i < j)
            a[j--] = a[i];
    }
    a[i] = x;
    return i;
}

//以栈的形式模拟递归
void Quick_Sort(int a[], int l, int t){
    stack<Pair>S;
    S.push(Pair(l, t));
    while(!S.empty()){//使用栈模拟
        int lt = S.top().first;
        int rt = S.top().second;
        S.pop();
        int mid = Partition(a, lt, rt);
        if(mid+1 < rt)
            S.push(Pair(mid+1, rt));
        if(lt < mid-1)
            S.push(Pair(lt, mid-1));
    }
}

4. 算法复杂度

空间复杂度：不管是递归版本，还是非递归版本，都会占用空间，复杂度为O(log2n) ~ O(n)，最好的情况是每次都是2分序列，复杂度为 O(log2n)，最差的情况是每次的枢纽值是最大值或最小值，复杂度为O(n)。

时间复杂度：平均情况下，有n个元素，栈的深度为 log2n，故总的时间复杂度为O(nlog2n)。

四、归并排序

1. 算法思想

归并排序是一种比较快的排序算法，是一种稳定排序算法。它也是采用分而治之的思想，归并排序是先划分排序元素，每次都是二分，先不进行比较，直到划分为单个元素后。回溯的时候进行比较，作归并。

如果还不懂，没关系！接下来看一下实例演示就懂了。

2. 实例演示

下面以数组 [5, 7, 9 , 3, 1, 8，6,2] 为例进行从小到大排序的演示：

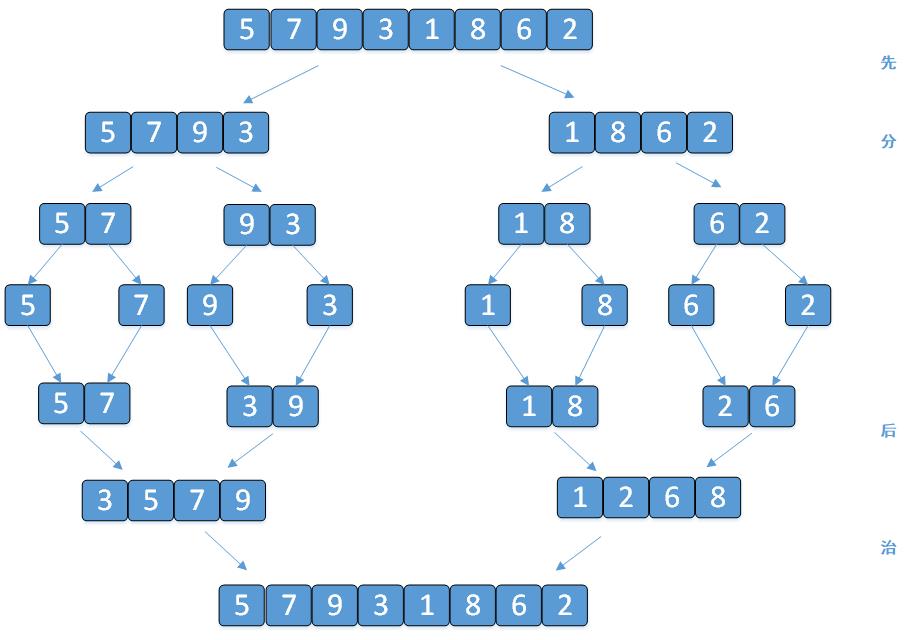
3. 代码演示

//归并排序的合并操作
void Merge(int a[], int lt, int rt, int p[]){//p是合并用的临时数组
    int mid = (rt - lt)/2 + lt;
    int i = lt, j = mid + 1;
    int k = 0;
    while(i <= mid && j <= rt){
        if(a[i] <= a[j]){
            p[k++] = a[i++];
        }else {
            p[k++] = a[j++];
        }
    }
    while(i <= mid){
        p[k++] = a[i++];
    }
    while(j <= rt){
        p[k++] = a[j++];
    }
    for(i = 0; i < k; ++i){
        a[lt+i] = p[i];
    }
}
//划分函数，递归划分
void MergeSort(int a[], int lt, int rt, int p[]){
    if(lt < rt){
        int mid = (rt - lt)/2 + lt;
        MergeSort(a, lt, mid, p);
        MergeSort(a, mid+1, rt, p);
        Merge(a, lt, rt, p);
    }
}

4. 算法复杂度

空间复杂度：在作合并的时候，需要一个辅助数组，故空间复杂度为O(n)；

时间复杂度：划分时，栈的深度为 log2n，时间复杂度为 O(log2n)，合并时，每次合并的时间复杂度为 O(n)，故总的时间复杂度为 O(nlog2n)。

五、堆排序

1. 算法思想

堆排序是一种不稳定的排序算法，适合于求第k大的数。

主要思想：以从小到大排序为例，先建立大顶堆，然后取出堆顶元素（堆顶元素一定是当前堆中的最大值），将堆的最后一个元素放置到堆顶。这时，并不是一个大顶堆，然后调整堆使其成为大顶堆，然后将堆顶元素取出，重复上述过程，一直到最后一个元素。

2. 实例演示

下面以数组 [5, 7, 9 , 3, 1, 8，6,2] 为例进行从小到大排序的演示：

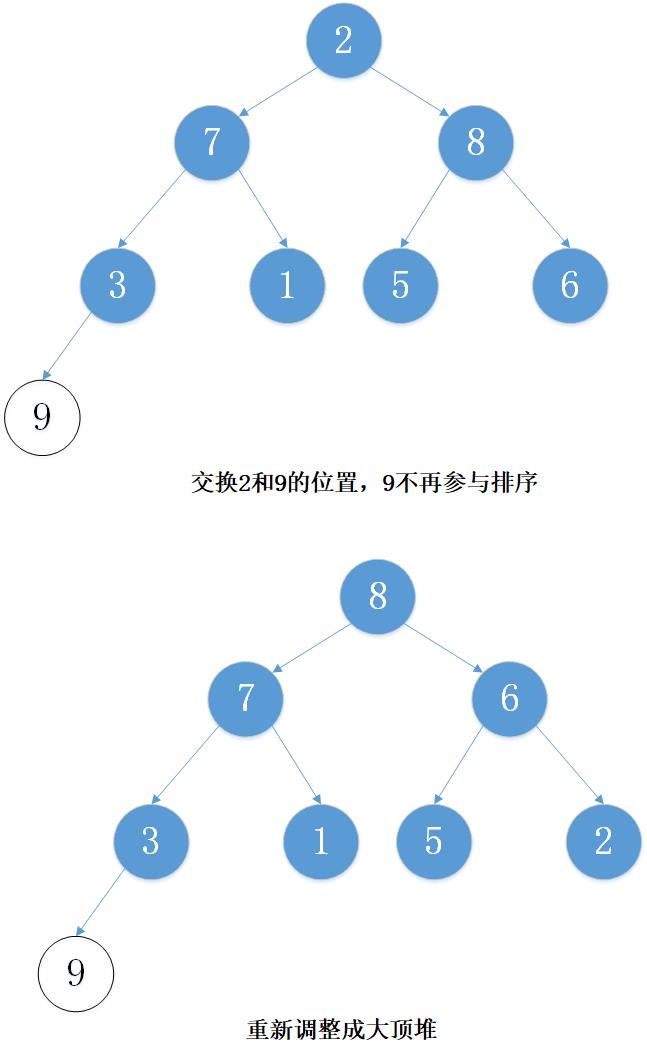
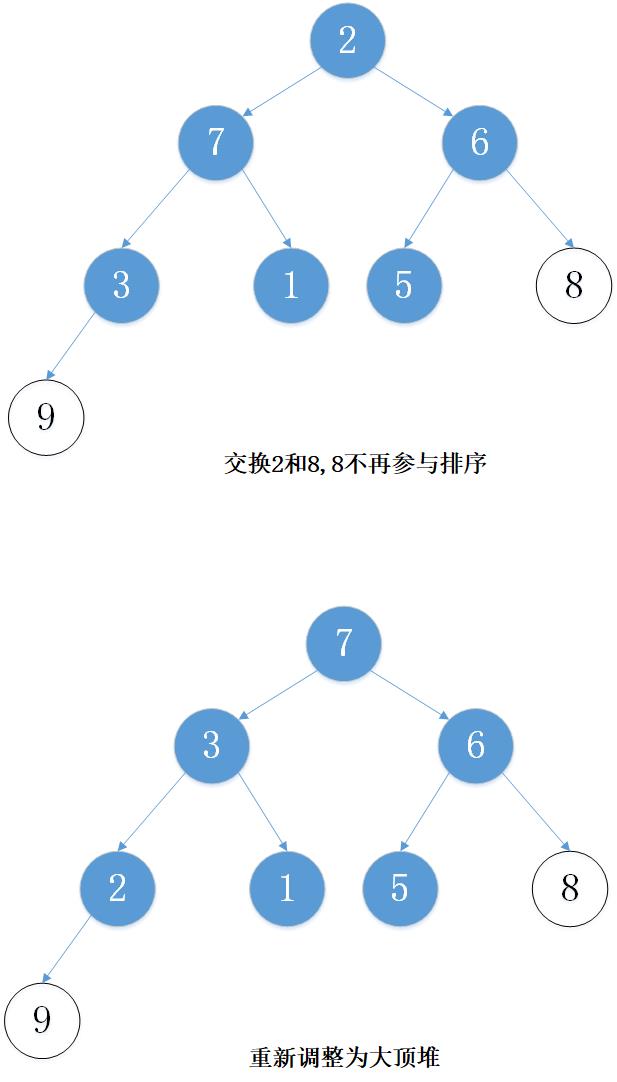
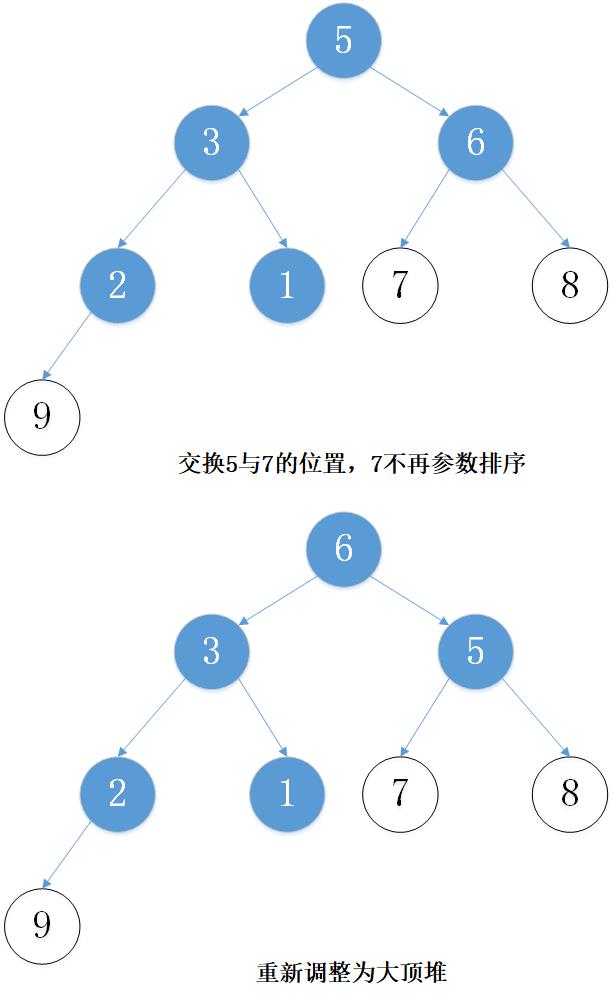
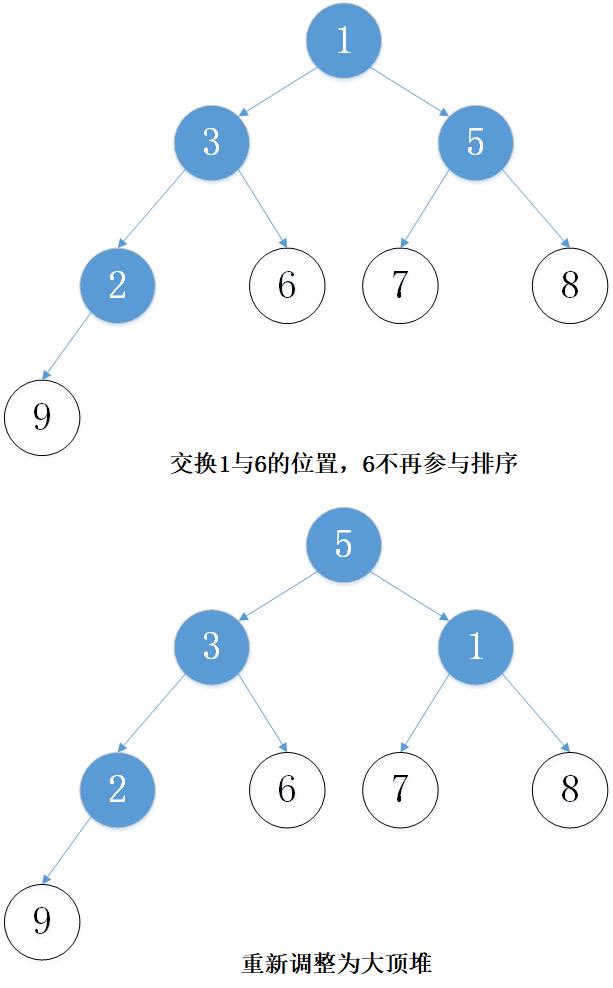
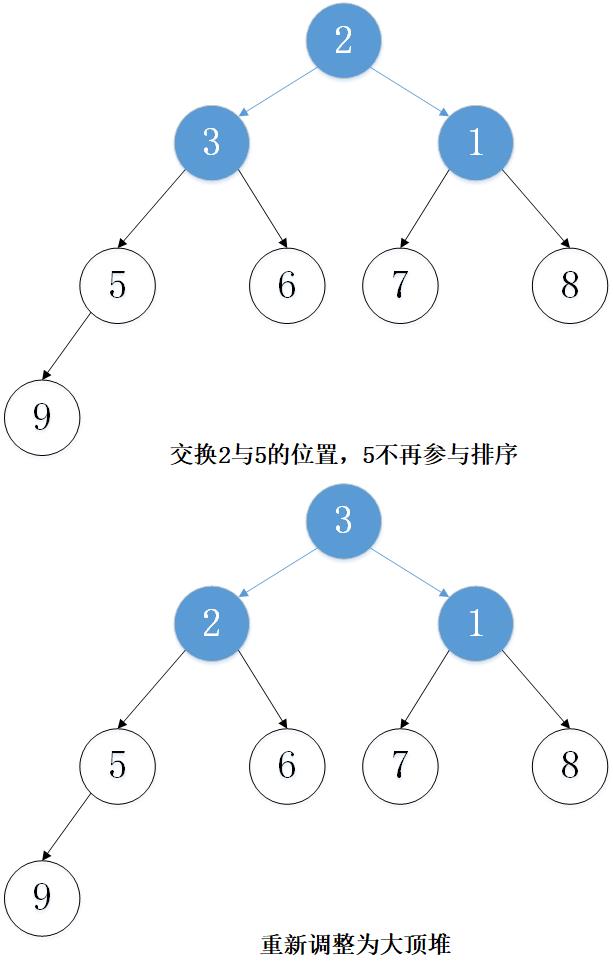
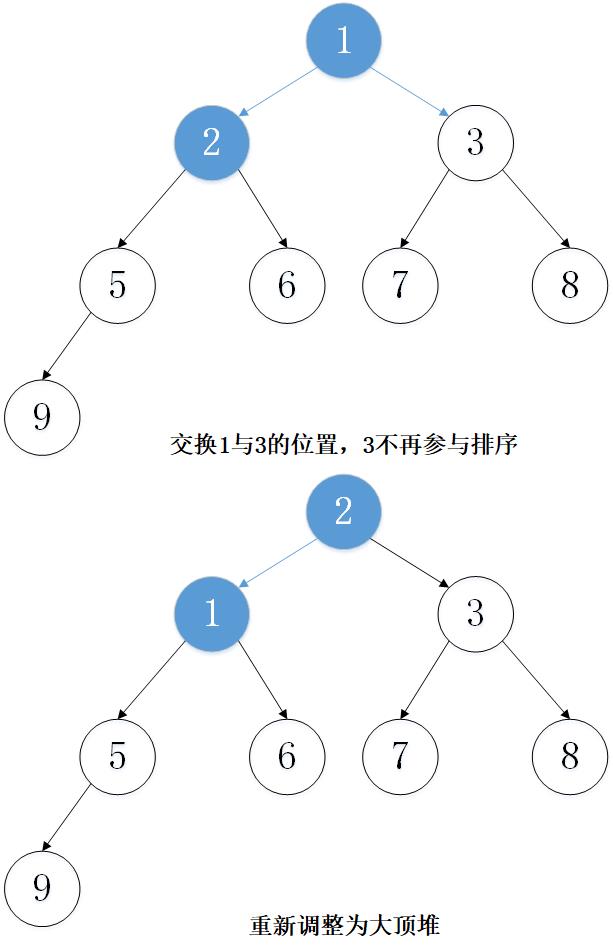
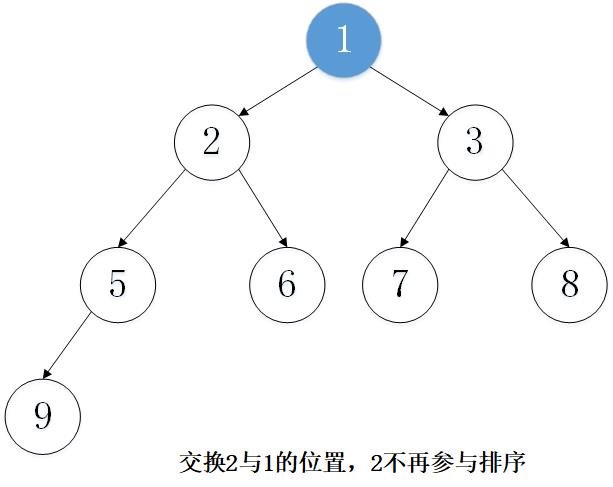
3. 代码实现

#include <iostream>

using namespace std;

//向下调整堆
void adjustHeap(int a[], int idx, int Len){
    while(idx*2+1 < Len){
        int temp = idx*2+1;
        if(temp+1 < Len && a[temp+1] > a[temp]){
            temp++;
        }
        if(a[idx] < a[temp]){
            swap(a[idx], a[temp]);
            idx = temp;
        }else break;
    }
}

/*
 * 堆排序
 * g[] : 待排序数组
 * n   : 元素个数
 */
void heapSort(int g[], int n){
    //先建立大顶堆
    for(int i = (n-1)/2; i >= 0; --i){
        adjustHeap(g, i, n);
    }
    //排序
    for(int i = 0;i < n; ++i){
        swap(g[0], g[n-i-1]);
        adjustHeap(g, 0, n-i-1);
    }
}

int main()
{
    int n = 8;
    int g[] = {5, 7, 9, 3, 1, 8, 6, 2};
    heapSort(g, n);
    for(int i = 0; i < n; ++i) {
        cout<<g[i]<<" ";
    }
    cout<<endl;
    return 0;
}

4. 算法复杂度

空间复杂度：在上述代码中，没有使用到额外的辅助空间，故空间复杂度为O(1)。

时间复杂度：在上述代码中，建立大顶堆的时间复杂度为O(n)，进行排序的时间复杂度为O(nlog2n)，故总的时间复杂度为O(nlog2n)。

六、直接插入排序

1. 算法思想

直接插入排序是一种很好理解的排序算法，是一种稳定的排序算法。

假设元素存储在数组 g 中，共有 n 个元素，依次遍历每一个元素，将元素 g[i] 按大小顺序插入到 0 ~ i 的位置。一直重复插入，直到第n个元素。

2. 实例演示

下面以数组 [7, 9, 5 , 3, 1] 为例进行从小到大排序的演示：

从第2个元素开始插入。

第2个元素插入：

9 比 7 大，所以 9 不需要移动位置，数组元素位置没有变化。

第3个元素插入：

经过比较，5 需要插入到 7 的前面，插入后的数组为：

[5, 7, 9, 3, 1]

第4个元素插入：

经过比较，3 需要插入到 5 的前面，插入后的数组为：

[3, 5, 7, 9, 1]

第5个元素插入：

经过比较，1 需要插入到 3 的前面，插入后的数组为：

[1, 3, 5, 7, 9]

数组已经有序了。

3. 代码实现

/*
 * 直接插入排序算法：
 * g ：待排序的数组
 * n ：数组的长度
 */
void directInsertSort(int g[], int n)
{
    for(int i = 1; i < n; ++i) { //依次遍历所有元素
        int j = i-1;
        int tmp = g[i];
        while(j >= 0 && g[j] > tmp) {
            g[j+1] = g[j];
            j--;
        }
        g[j+1] = tmp;
    }
}

4. 算法复杂度

空间复杂度：除了本身的数组不需要额外的存储空间，故空间复杂度为 O(1)。

时间复杂度：需要排序的元素的时间复杂度为 O(n)，对应第一层 for 循环，每插入一个元素的时间复杂度为O(n)，对应while循环，故总的时间复杂度为 O(n^2)。

七、希尔排序

1. 算法思想

希尔排序是将元素进行分组插入排序的算法，是一种不稳定的排序算法。

主要思想：间隔以数组长度每次除以2为例。数组中的元素先以n/2为间隔分组，每个分组使用插入排序算法的思想进行排序，排序后每个分组中的元素是有序的，然后，将间隔设为 n/2/2 进行分组，每个分组使用插入排序算法思想进行排序，后面重复上述过程，直到间隔为1。间隔为1时和插入排序算法一样了。

2. 实例演示

下面以数组 [35, 51, 20, 0, 231, 100, 92, 27, 789, 9] 为例进行从小到大排序的演示：

我们以数组长度每次除2为间隔（step），上述数组 n = 10。

第一次，step = 10/2 = 5

那么，会分成如下几组：

(35, 100), (51, 92), (20, 27), (0, 789), (231, 9)

每组经过插入排序后，结果为：

(35, 100), (51, 92), (20, 27), (0, 789), (9, 231)

排序后的数组为：

[35, 51, 20, 0, 9, 100, 92, 27, 789, 231]

第二次，step = 5/2 = 2

那么，会分成如下几组：

(35, 20, 9, 92, 789), (51, 0, 100, 27, 231)

每组经过插入排序后，结果为：

(9, 20, 35, 92, 789), (0, 27, 51, 100, 231)

排序后的数组为:

[9, 0, 20, 27, 35, 51, 92, 100, 789, 231]

第三次，step = 2/2 = 1

那么，整个数组就是一个分组，直接进行插入排序了，排序后的结果为：

[0, 9, 20, 27, 35, 51, 92, 100, 231, 789]

3. 代码实现

#include <iostream>
using namespace std;

void shellSort(int g[], int n) {
    //每次排序间隔的步数
    for(int step = n >> 1; step > 0; step = step >> 1) {
        for(int i = step; i < n; ++i) {//对间隔为 step 的各个分组进行插入排序
            if(g[i] < g[i-step]) {//小于分组中前一个元素的情况下才排序，否则已有序
                int j = i;
                int tmp = g[j];
                while(j-step >= 0 && g[j] < g[j-step]) {
                    g[j] = g[j-step];
                    j -= step;
                }
                g[j] = tmp;
            }
        }
    }
}


int main()
{
    int n = 10;
    int g[] = {35, 51, 20, 0, 231, 100, 92, 27, 789, 9};
    shellSort(g, n);
    for(int i = 0; i < n; ++i) {
        cout<<g[i]<<" ";
    }
    cout<<endl;
    return 0;
}

4. 算法复杂度

空间复杂度：在上述代码中，没有使用到额外的空间，空间复杂度为O(1)。

时间复杂度：希尔排序的时间复杂度为O(n^(1.3 - 2))。

八、基数排序

1. 算法思想

基数排序是一种比较容易理解的排序，是一种稳定的排序算法。

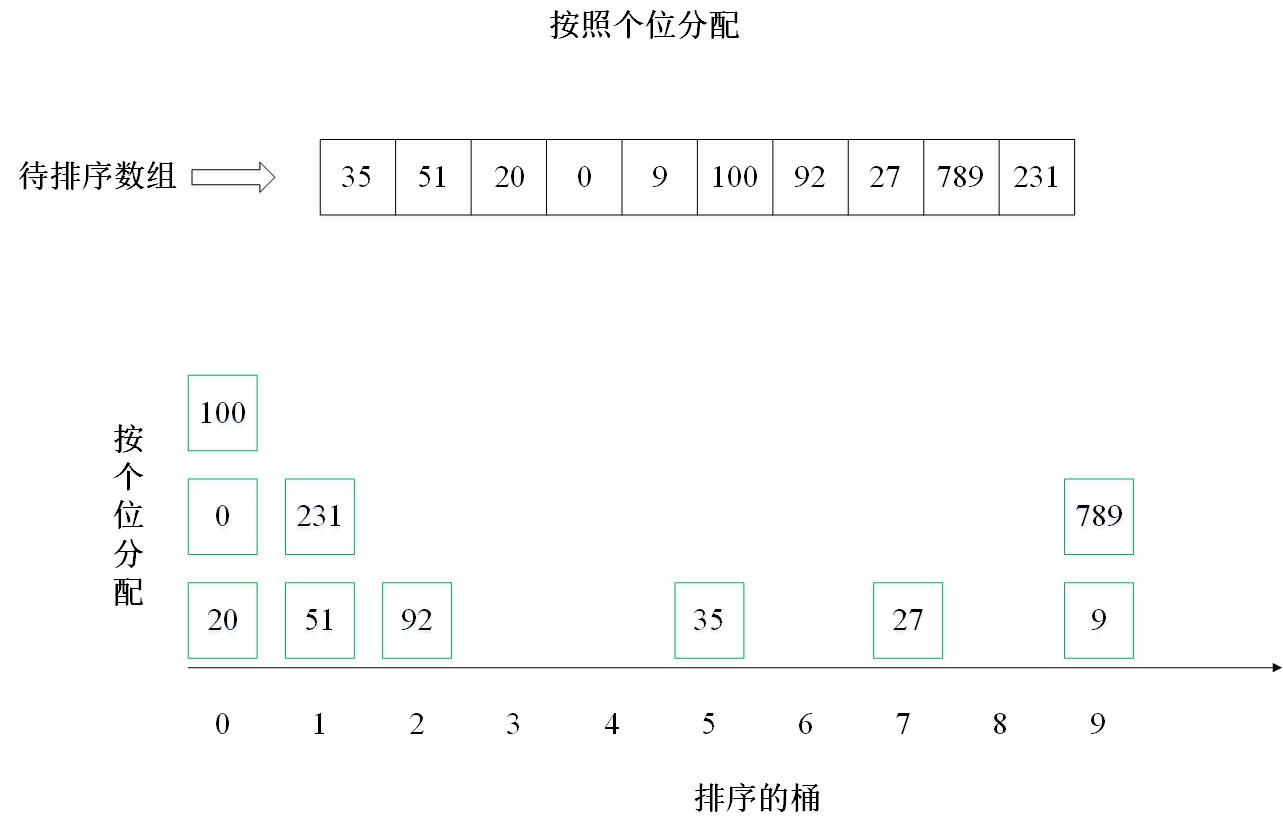
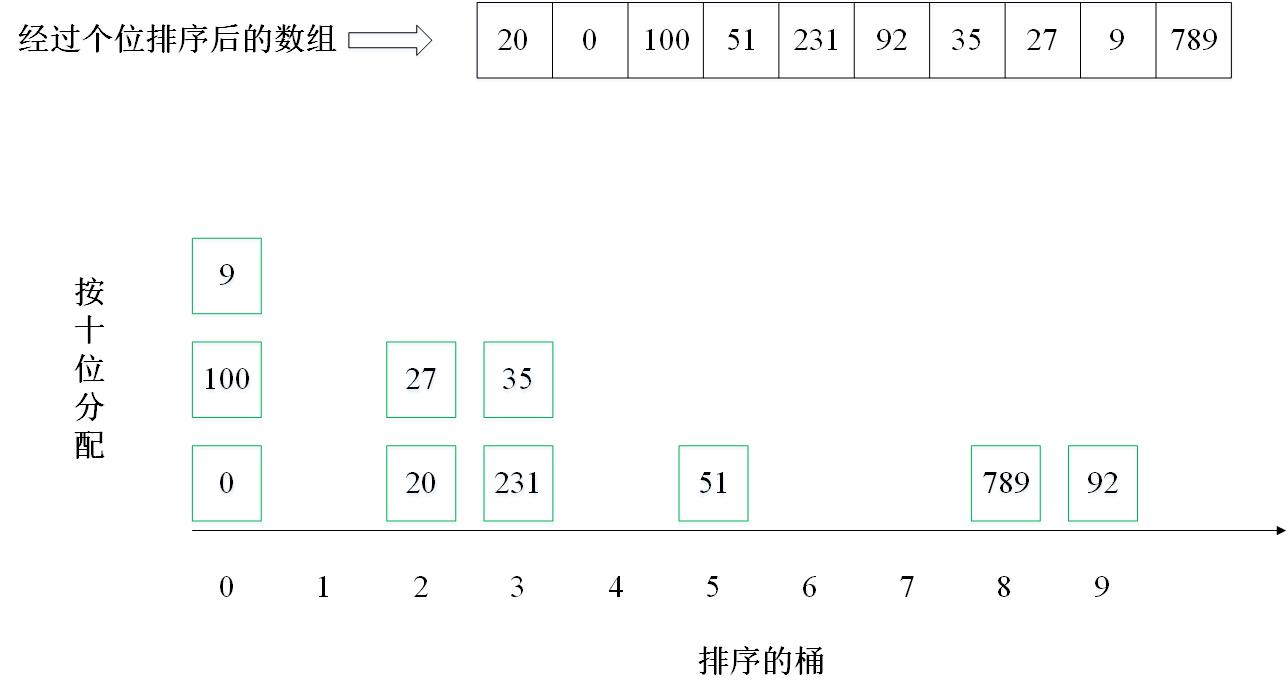
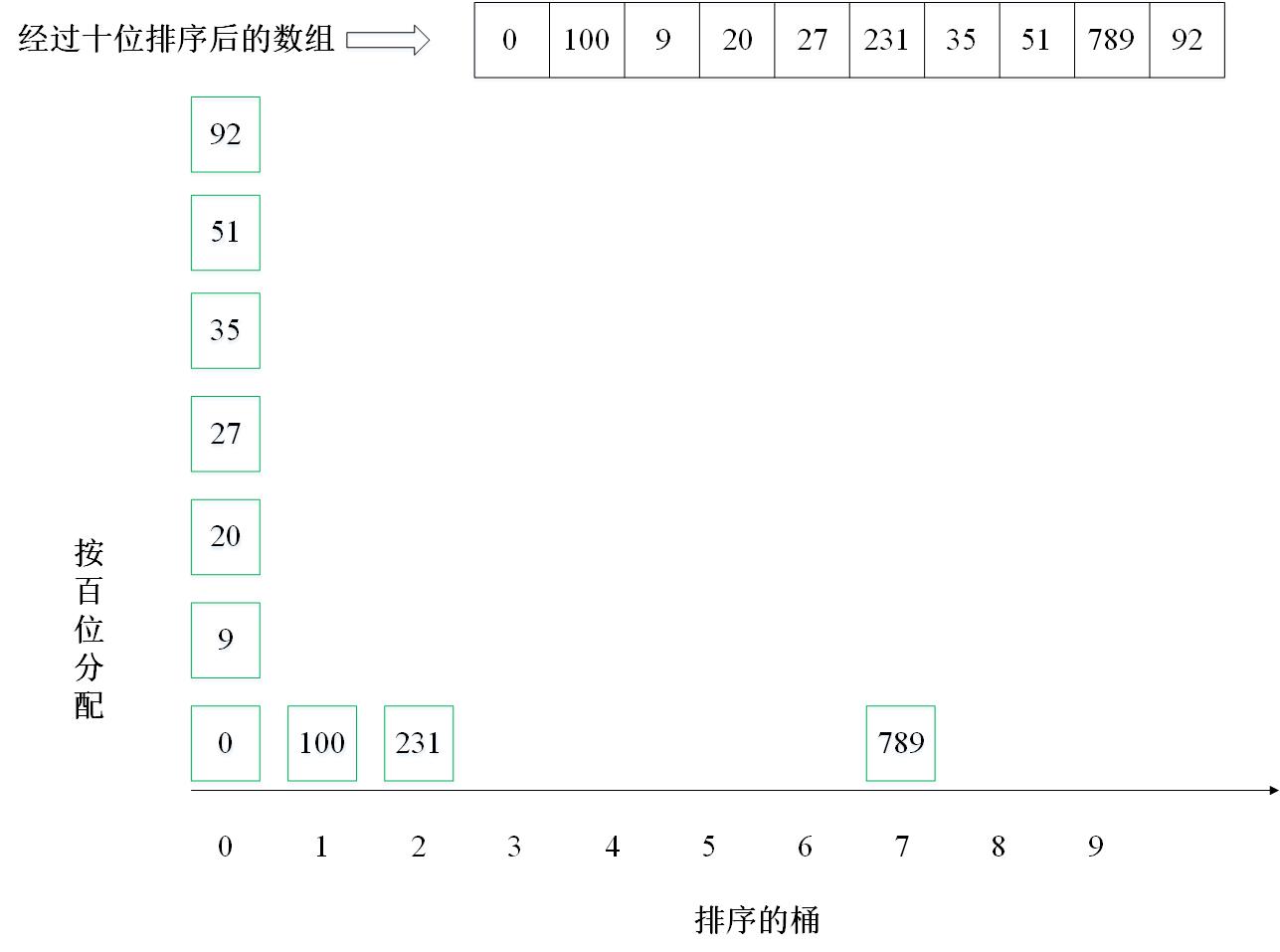
主要思想：按照数字的位数进行排序，即：先排个位，再排十位，再排百位……。有10个桶，标号为0~9。排序个位时，按照个位值的不同，分配到10个桶中（0分配到0号桶，1分配到1号桶，以此类推），然后将分配后的结果收集，这时候数组是按照个位排序的。继续按照十位重复上述排序过程，一直排序完所有的位数（取决于数组中最大数的位数）。

2. 实例演示

下面以数组 [35, 51, 20, 0, 9, 100, 92, 27, 789, 231] 为例进行从小到大排序的演示：

3. 代码实现

#include <iostream>
#include <vector>
using namespace std;

//求数组中值的最大位数
int maxBit(int g[], int n)
{
    //找出最大数
    int maxVal = g[0];
    for (int i = 1; i < n; ++i){
        maxVal = max(maxVal, g[i]);
    }

    //计算最大数的位数
    int num = 0;
    while(maxVal) {
        ++num;
        maxVal /= 10;
    }
    return num ? num : 1;
}

void radixSort(int g[], int n) //基数排序
{
    int p = 1;
    int d = maxBit(g, n);
    vector<int>bucket[10];
    for(int i = 0; i < d; ++i) {
        //清空存储值的桶
        for(int j = 0; j < 10; j++) {
            bucket[j].clear();
        }
        //将每个元素分到对应桶里
        for(int j = 0; j < n; ++j) {
            int k = (g[j]/p)%10;
            bucket[k].push_back(g[j]);
        }
        //将桶里的数依次取出
        int idx = 0;
        for(int j = 0; j < 10; ++j) {
            for(int k = 0; k < (int)bucket[j].size(); ++k) {
                g[idx++] = bucket[j][k];
            }
        }
        p *= 10;
    }
}

int main()
{
    int n = 10;
    int g[] = {35, 51, 20, 0, 9, 100, 92, 27, 789, 231};
    radixSort(g, n);

    for(int i = 0; i < n; ++i) {
        cout<<g[i]<<" ";
    }
    cout<<endl;
    return 0;
}

4. 算法复杂度

空间复杂度：在上述代码中，使用到了一个vector数组来辅助排序，故空间复杂度为O(d+n)；

时间复杂度：在上述代码中，要遍历最大位数 d（第一层 for 循环），每次遍历次数需要遍历整个排序数组，因为两者是嵌套的关系，故总的时间复杂度为O(dn)。

🎈 欢迎小伙伴们点赞👍、收藏⭐、留言💬

以上是关于万字整理❤️8大排序算法❤️建议收藏的主要内容，如果未能解决你的问题，请参考以下文章

❤️五万字《十大排序算法》动图讲解❤️(建议收藏)

❤️❤️新生代农民工爆肝8万字，整理Python编程从入门到实践(建议收藏)已码：8万字❤️❤️

❤️❤️爆肝3万字整理小白入门与提升分布式版本管理软件：Git，图文并茂(建议收藏)--已码一万字❤️❤️

苏州程序大白用2万字解析数据结构和八大排序算法☀️《❤️记得收藏❤️》

七万字❤️零基础学算法 LeetCode 热题 HOT 100（附题解，强烈建议收藏）

❤️爆肝万字整理的综合架构web服务之nginx详解❤️，附建议收藏