二维数组5：矩阵置零的三种解法

Posted 2021-08-27 纵横千里，捭阖四方

 leetcode73，给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。

进阶：

一个直观的解决方案是使用  O(mn) 的额外空间，但这并不是一个好的解决方案。

一个简单的改进方案是使用 O(m + n) 的额外空间，但这仍然不是最好的解决方案。

你能想出一个仅使用常量空间的解决方案吗？

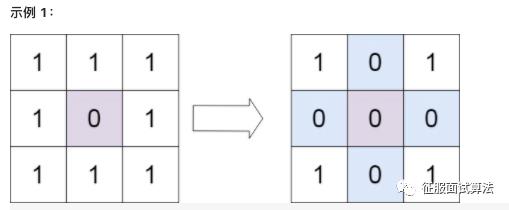
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]输出：[[1,0,1],[0,0,0],[1,0,1]]

输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

 这个题目可以说比较明显的是三种思路：使用数组标记，使用一个变量标记和使用两个变量标记。

一.使用数组标记

最笨的方式是使用一个相同大小的二维数组来标记，但是已经被题目要求毙了。我们先看一下如何用两个标记数组分别记录每一行和每一列是否有零出现。

具体地，我们首先遍历该数组一次，如果某个元素为 0，那么就将该元素所在的行和列所对应标记数组的位置置为 true。最后我们再次遍历该数组，用标记数组更新原数组即可。

class Solution {    public void setZeroes(int[][] matrix) {        int m = matrix.length, n = matrix[0].length;        boolean[] row = new boolean[m];        boolean[] col = new boolean[n];        for (int i = 0; i < m; i++) {            for (int j = 0; j < n; j++) {                if (matrix[i][j] == 0) {                    row[i] = col[j] = true;                }            }        }        for (int i = 0; i < m; i++) {            for (int j = 0; j < n; j++) {                if (row[i] || col[j]) {                    matrix[i][j] = 0;                }            }        }    }}

二.使用两个标记变量

上面的方法在题目要求里说不是最优的，那我们考虑一下是否进一步降低开辟空间的大小。

我们可以用矩阵的第一行和第一列代替方法一中的两个标记数组，以达到 O(1)的额外空间。但这样会导致原数组的第一行和第一列被修改，无法记录它们是否原本包含 0。因此我们需要额外使用两个标记变量分别记录第一行和第一列是否原本包含 0。

在代码中，我们首先预处理出两个标记变量，接着使用其他行与列去处理第一行与第一列，然后反过来使用第一行与第一列去更新其他行与列，最后使用两个标记变量更新第一行与第一列即可。

class Solution {    public void setZeroes(int[][] matrix) {        int m = matrix.length, n = matrix[0].length;        boolean flagCol0 = false, flagRow0 = false;        //检查第一列有没有0        for (int i = 0; i < m; i++) {        //第一列有0，就标记一下            if (matrix[i][0] == 0) {                flagCol0 = true;            }        }        //检查第一行有没有0        for (int j = 0; j < n; j++) {         //第一列有0，就标记一下            if (matrix[0][j] == 0) {                flagRow0 = true;            }        }        //标记之后，第一行和第一列的原有元素就不重要了，能被覆盖        //可以用来代替上一种方法里的row和col数组        //接下来的逻辑与方法一种的是一样的了        for (int i = 1; i < m; i++) {            for (int j = 1; j < n; j++) {                if (matrix[i][j] == 0) {                    matrix[i][0] = matrix[0][j] = 0;                }            }        }        for (int i = 1; i < m; i++) {            for (int j = 1; j < n; j++) {                if (matrix[i][0] == 0 || matrix[0][j] == 0) {                    matrix[i][j] = 0;                }            }        }        //最后再根据两个标记决定是否将第一行或第一列也清空，        if (flagCol0) {            for (int i = 0; i < m; i++) {                matrix[i][0] = 0;            }        }        if (flagRow0) {            for (int j = 0; j < n; j++) {                matrix[0][j] = 0;            }        }    }}

如果能做到这种程度，面试基本就能过关了。我还找到只使用一个变量的方法，但是为了省一个变量牺牲了很多脑细胞，真不知道值不值，至少工程里不要这么干，会被同事骂。

  三.使用一个标记变量

这个方法感觉会前面两个就足够了，这个理解有点难。

我们可以对方法二进一步优化，只使用一个标记变量记录第一列是否原本存在 0。

我们上面介绍的方式用了两个变量，分别表示第一行和第一列是否出现了0。如果采用一个变量的话，我们用该变量表示第一列是否出现0，而第一行是否出现怎么办呢？我们用matrix[0][0]来表示。这里的问题就是如何保证该位置不被提前覆盖了呢?方法就是从最后一行开始，倒序地处理矩阵元素。

class Solution {    public void setZeroes(int[][] matrix) {        int m = matrix.length, n = matrix[0].length;        boolean flagCol0 = false;        //这里主要处理第一列的情况        for (int i = 0; i < m; i++) {        //只要第一列中某个位置出现了0，则第一列最后就会被置0            if (matrix[i][0] == 0) {                flagCol0 = true;            }            //判断每一行是否出现了0，有则将该该元素对应的行和列位置设置为0            for (int j = 1; j < n; j++) {                if (matrix[i][j] == 0) {                //将第一行是否有0存到matrx[0][0]里了                    matrix[i][0] = matrix[0][j] = 0;//①                }            }        }        //②这里开始根据第一样和第一列的标记清理数组        for (int i = m - 1; i >= 0; i--) {            for (int j = 1; j < n; j++) {                if (matrix[i][0] == 0 || matrix[0][j] == 0) {                    matrix[i][j] = 0;//③                }            }            if (flagCol0) {                matrix[i][0] = 0;            }        }    }}

在上面的代码中，大部分过程与前面的类似，我们重点关注i=0时的情况，

在①处，很明显是。

对于②之后的部分，为了方便，当i=0时，代码可以简化成这样：

 for (int j = 1; j < n; j++) {     if (matrix[0][0] == 0 || matrix[0][j] == 0) {         matrix[0][j] = 0;//③     }    }    if (flagCol0) {       matrix[0][0] = 0;      } }

这里的点睛之笔是判断条件的前部分：

if (matrix[0][0] == 0 || matrix[0][j] == 0)

 如果matrix[0][0]是0，不管matrix[0][j]是啥，第一行都变成0了，反之则不受影响。这其实就是用matrx[0][0]来标记第一行是否为0，有则清理，从而实现用matrx[0][0]来代替标记第一行是否为0的变量。

这个方法非常巧妙，但是除了面试时装(A+C)/2，不知道有啥用。