凑零钱问题的三种解法(Java)

Posted 2021-10-09 结构化思维wz

文章目录

• • 问题描述：
  • 1.递归解法
  • 2.带备忘录的递归解法
  • 3.dp数组动态规划解法

问题描述：

    给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。
你可以认为每种硬币的数量是无限的。

示例 1：
输入：coins = [1, 2, 5], amount = 11
输出：3 
解释：11 = 5 + 5 + 1

示例 2：
输入：coins = [2], amount = 3
输出：-1

1.递归解法

/**
 * @author 王泽
 * 凑硬币的核心思路，把所有可以凑的方案穷举出来，然后找使用硬币最少的。
 * 动态规划问题，要符合最优子结构，子问题间必须互相独立。
 */

public class CoinChange1 {

    /**
     * 暴力递归
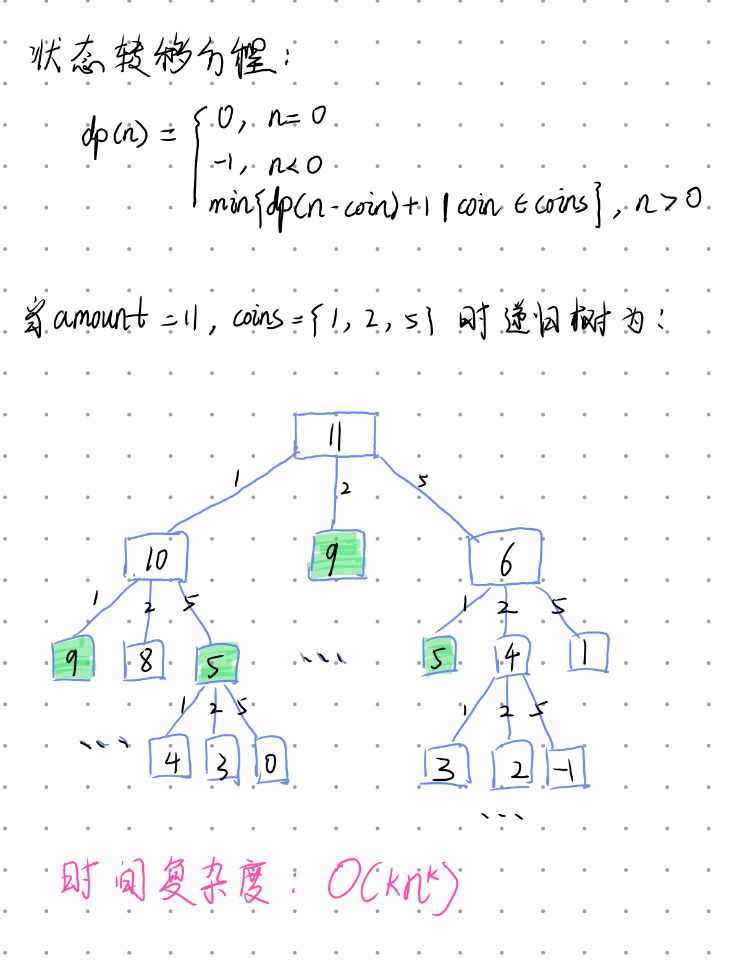
     * 列出正确的状态转移方程
     * 1.确定base case：amount为0，返回0.
     * 2.确定状态，也就是原问题和子问题中的变量：amount
     * 3.确定选择：也就是导致“状态”产生变化的行为。（硬币的选择就是导致状态变化的行为）
     * 4.明确dp函数/数组的定义
     * @param coins
     * @param amount
     *
     * 伪代码思路：
     *      public int coinChange(int[] coins, int amount){
     *          return dp(coins,amount);
     *      }
     *      int dp(int[] coins, int amount){
     *          for(int coin : coins){
     *              res = min(res,1+dp(amount-coin));
     *          }
     *          return res;
     *      }
     */


    public int coinChange(int[] coins, int amount) {
        // 题目要求的最终结果是 dp(amount)
        return dp(coins, amount);
    }

    private int dp(int[] coins, int amount) {
        // base case
        if (amount == 0) {
            return 0;
        }
        if (amount < 0) {
            return -1;
        }

        //初始化res为Integer中最大值
        int res = Integer.MAX_VALUE;
        for (int coin : coins) {
            // 计算子问题的结果
            int subProblem = dp(coins, amount - coin);
            // 子问题无解则跳过
            if (subProblem == -1) {
                continue;
            }
            // 在子问题中选择最优解，然后加一
            res = Math.min(res, subProblem + 1);
        }

        // 没有最优解，返回-1
        return res == Integer.MAX_VALUE ? -1 : res;
    }

}

2.带备忘录的递归解法

import java.util.Arrays;

/**
 * @author 王泽
 * 带备忘录的递归
 * 时间复杂度O(kn)
 */

public class CoinChange2 {
     //定义备忘录数组
    int[] memo;

    public int coinChange(int[] coins, int amount) {
        memo = new int[amount + 1];
        // dp 数组全都初始化为特殊值，将array数组的所有数值都赋值为value -666
        Arrays.fill(memo, -666);
        return dp(coins, amount);
    }

    private int dp(int[] coins, int amount) {
        if (amount == 0) {
            return 0;
        }
        if (amount < 0) {
            return -1;
        }
        // 查备忘录，防止重复计算
        if (memo[amount] != -666) {
            return memo[amount];
        }

        int res = Integer.MAX_VALUE;
        for (int coin : coins) {
            // 计算子问题的结果
            int subProblem = dp(coins, amount - coin);
            // 子问题无解则跳过
            if (subProblem == -1) {
                continue;
            }
            // 在子问题中选择最优解，然后加一
            res = Math.min(res, subProblem + 1);
        }
        // 把计算结果存入备忘录
        memo[amount] = (res == Integer.MAX_VALUE) ? -1 : res;
        return memo[amount];
    }


}

3.dp数组动态规划解法

import java.util.Arrays;

/**
 * @author 王泽
 * 动态规划解法.
 * 把目标金额作为变量，体现在数组索引上。
 * dp数组的定义：当目标金额为 amount时，需要dp[amount]枚硬币才能凑出。
 */

public class CoinChange3 {

    public int coinChange(int[] coins, int amount) {
        // 凑成amount最多用amount(全用1元的硬币)枚硬币，所以初始化为amount+1 就相当于初始化为正无穷，方便以后选小的。
        int[] dp = new int[amount + 1];
        // 数组大小为 amount + 1，初始值也为 amount + 1
        Arrays.fill(dp, amount + 1);

        // base case
        dp[0] = 0;
        // 外层 for 循环在遍历所有状态的所有取值
        for (int i = 0; i < dp.length; i++) {
            // 内层 for 循环在求所有选择的最小值
            for (int coin : coins) {
                // 子问题无解，跳过
                if (i - coin < 0) {
                    continue;
                }
                dp[i] = Math.min(dp[i], 1 + dp[i - coin]);
            }
        }
        return (dp[amount] == amount + 1) ? -1 : dp[amount];
    }


}