机器学习EM算法
Posted ZSYL
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习EM算法相关的知识,希望对你有一定的参考价值。
EM算法
1. 初识EM算法
EM算法也称期望最大化(Expectation-Maximum,简称EM)算法。
它是⼀个基础算法,是很多机器学习领域算法的基础,⽐如隐式⻢尔科夫算法(HMM)等等。
EM算法是⼀种迭代优化策略,由于它的计算⽅法中每⼀次迭代都分两步,
- 其中⼀个为期望步(E步),
- 另⼀个为极大步(M步),
所以算法被称为EM算法(Expectation-Maximization Algorithm)。
EM算法受到缺失思想影响,最初是为了解决数据缺失情况下的参数估计问题,其算法基础和收敛有效性等问题在Dempster、Laird和Rubin三⼈于1977年所做的⽂章《Maximum likelihood from incomplete data via the EM algorithm》 中给出了详细的阐述。其基本思想是:
- ⾸先根据⼰经给出的观测数据,估计出模型参数的值;
- 然后再依据上⼀步估计出的参数值估计缺失数据的值,再根据估计出的缺失数据加上之前⼰经观测到的数据重新再 对参数值进⾏估计;
- 然后反复迭代,直⾄最后收敛,迭代结束。
EM算法计算流程:
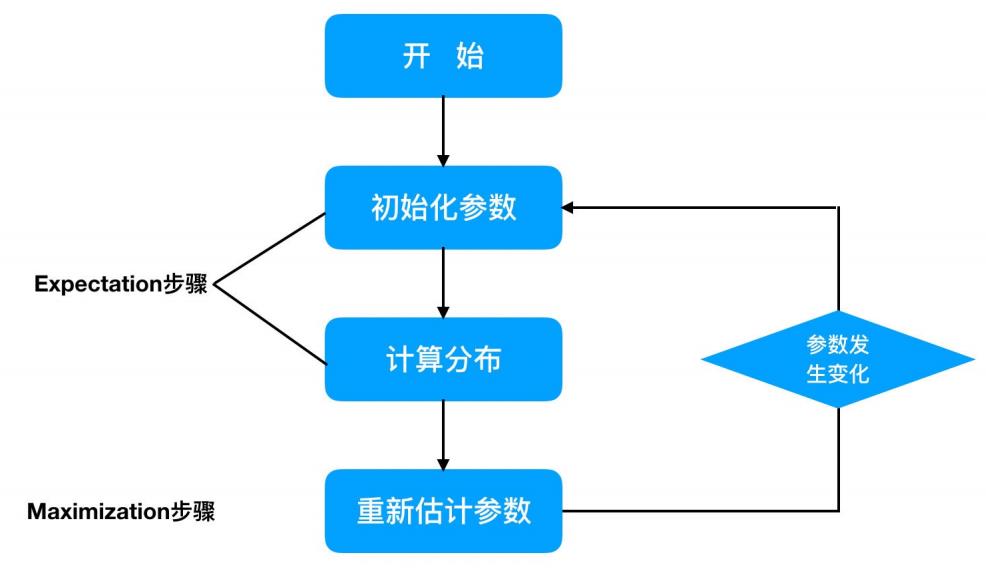
小结
- EM算法是⼀种迭代优化策略,由于它的计算⽅法中每⼀次迭代都分两步:
- 其中⼀个为期望步(E步)
- 另⼀个为极⼤步(M步)
2. EM算法介绍
想清晰的了解EM算法,我们需要知道⼀个基础知识:
- “极⼤似然估计”
2.1 极大似然估计
2.1.1 问题描述
假如我们需要调查学校的男⽣和⼥⽣的身⾼分布 ,我们抽取100个男⽣和100个⼥⽣,将他们按照性别划分为两组。
然后,统计抽样得到100个男⽣的身⾼数据和100个⼥⽣的身⾼数据。
如果我们知道他们的身⾼服从正态分布,但是这个分布的均值μ 和⽅差δ 是不知道,这两个参数就是我们需要估计的。
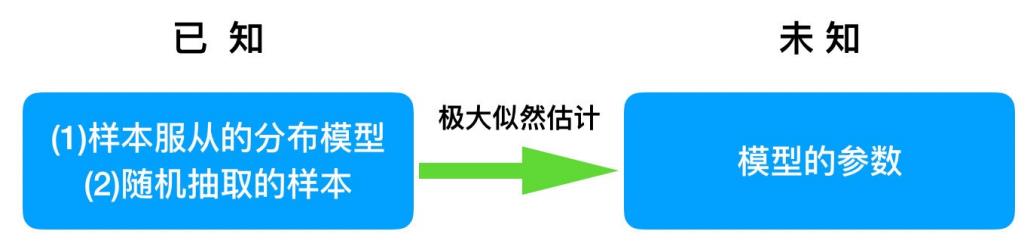
问题:我们知道样本所服从的概率分布模型和⼀些样本,我们需要求解该模型的参数.
-
我们已知的条件有两个:
- 样本服从的分布模型
- 随机抽取的样本。
-
我们需要求解模型的参数。
根据已知条件,通过极大似然估计,求出未知参数。
总的来说:极大似然估计就是用来估计模型参数的统计学方法。
2.1.2 用数学知识解决现实问题
问题数学化:
-
样本集
-
概率密度是:P(xi|si)抽到第i个男生身高的概率。
-
由于100个样本之间独立同分布,所以同时抽到这100个男⽣的概率是它们各⾃概率的乘积,也就是样本集X中各个 样本的联合概率,用下式表示:
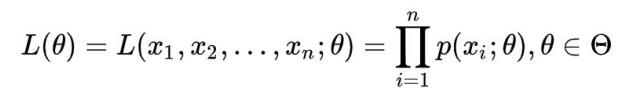
- 这个概率反映了在概率密度函数的参数是θ时,得到X这组样本的概率。
- 我们需要找到⼀个参数θ,使得抽到X这组样本的概率最大,也就是说需要其对应的似然函数L(θ)最大。
- 满足条件的θ叫做θ的最大似然估计值,记为:
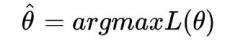
- 满足条件的θ叫做θ的最大似然估计值,记为:
2.1.3 最大似然函数估计值的求解步骤

多数情况下,我们是根据已知条件来推算结果,而极大似然估计是已知结果,寻求使该结果出现的可能性最大的条件, 以此作为估计值。
2.2 EM算法实例描述
我们⽬前有100个男⽣和100个⼥⽣的身⾼,但是我们不知道这200个数据中哪个是男⽣的身⾼,哪个是⼥⽣的身⾼,即 抽取得到的每个样本都不知道是从哪个分布中抽取的。
这个时候,对于每个样本,就有两个未知量需要估计:
(1)这个身⾼数据是来⾃于男⽣数据集合还是来⾃于⼥⽣?
(2)男⽣、⼥⽣身⾼数据集的正态分布的参数分别是多少?
具体问题如下图:
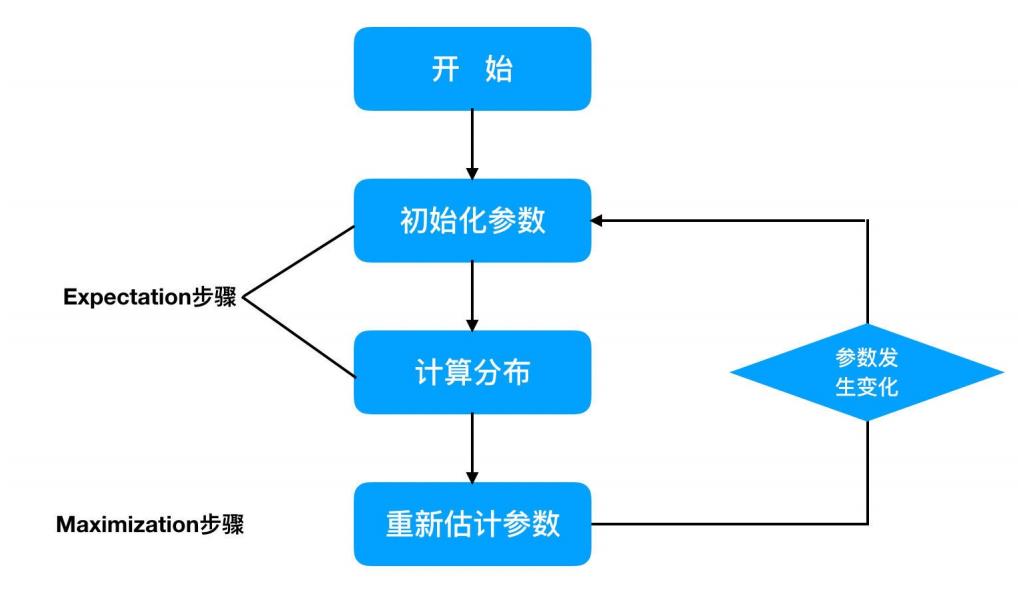
(1)初始化参数:先初始化男⽣身⾼的正态分布的参数:如均值=1.65,⽅差=0.15;
(2)计算分布:计算每⼀个⼈更可能属于男⽣分布或者⼥⽣分布;
(3)重新估计参数:通过分为男⽣的n个⼈来重新估计男⽣身⾼分布的参数(最⼤似然估计),⼥⽣分布也按照相同的 ⽅式估计出来,更新分布。
(4)这时候两个分布的概率也变了,然后重复步骤(1)⾄(3),直到参数不发⽣变化为⽌。
3. EM算法实例
3.1 ⼀个超级简单的案例
假设现在有两枚硬币1和2,,随机抛掷后正⾯朝上概率分别为P1,P2。为了估计这两个概率,做实验,每次取⼀枚硬 币,连掷5下,记录下结果,如下:
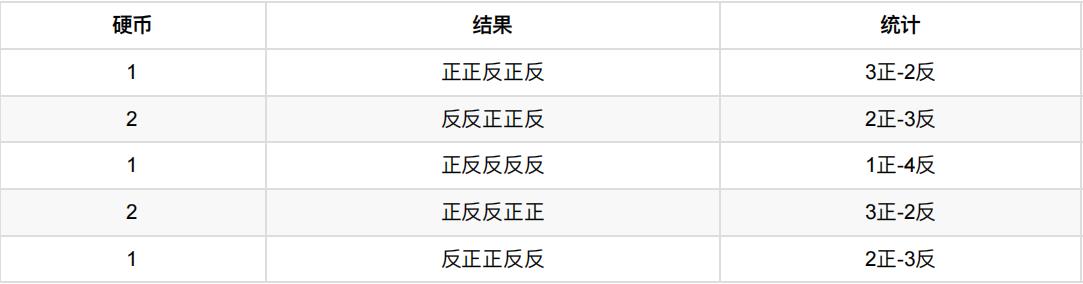
可以很容易地估计出P1和P2,如下:
P1 = (3+1+2)/ 15 = 0.4 P2= (2+3)/10 = 0.5
到这⾥,⼀切似乎很美好,下⾯我们加⼤难度。
3.2 加入隐变量z后的求解
还是上⾯的问题,现在我们抹去每轮投掷时使⽤的硬币标记,如下:
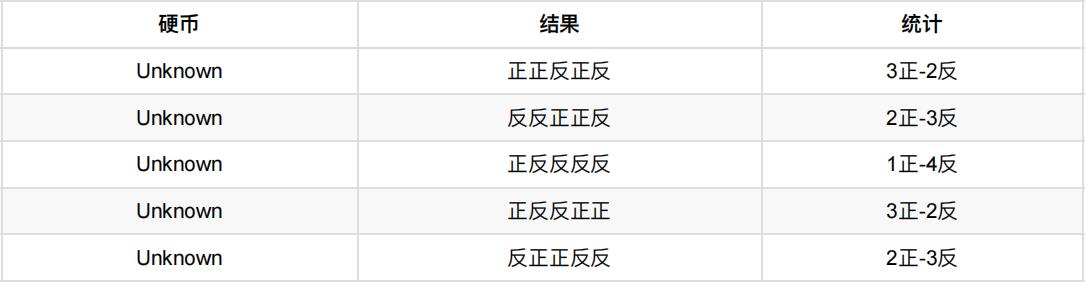
好了,现在我们的⽬标没变,还是估计P1和P2,要怎么做呢?
显然,此时我们多了⼀个隐变量z,可以把它认为是⼀个5维的向量(z1,z2,z3,z4,z5),代表每次投掷时所使⽤的硬币, ⽐如z1,就代表第⼀轮投掷时使⽤的硬币是1还是2。但是,这个变量z不知道,就⽆法去估计P1和P2,所以,我们必须 先估计出z,然后才能进⼀步估计P1和P2。
但要估计z,我们⼜得知道P1和P2,这样我们才能⽤最⼤似然概率法则去估计z,这不是鸡⽣蛋和蛋⽣鸡的问题吗,如何破?
答案就是先随机初始化⼀个P1和P2,⽤它来估计z,然后基于z,还是按照最⼤似然概率法则去估计新的P1和P2,如果 新的P1和P2和我们初始化的P1和P2⼀样,请问这说明了什么?(此处思考1分钟)
这说明我们初始化的P1和P2是⼀个相当靠谱的估计!
就是说,我们初始化的P1和P2,按照最⼤似然概率就可以估计出z,然后基于z,按照最⼤似然概率可以反过来估计出 P1和P2,当与我们初始化的P1和P2⼀样时,说明是P1和P2很有可能就是真实的值。这⾥⾯包含了两个交互的最⼤似然估计。
如果新估计出来的P1和P2和我们初始化的值差别很⼤,怎么办呢?就是继续⽤新的P1和P2迭代,直⾄收敛。
这就是下⾯的EM初级版。
3.2.1 EM初级版
我们不妨这样,先随便给P1和P2赋⼀个值,⽐如:
- P1 = 0.2
- P2 = 0.7
然后,我们看看第⼀轮抛掷最可能是哪个硬币。
- 如果是硬币1,得出3正2反的概率为 0.2 ∗ 0.2 ∗ 0.2 ∗ 0.8 ∗ 0.8 = 0.00512
- 如果是硬币2,得出3正2反的概率为0.7 ∗ 0.7 ∗ 0.7 ∗ 0.3 ∗ 0.3 = 0.03087
然后依次求出其他4轮中的相应概率。做成表格如下:
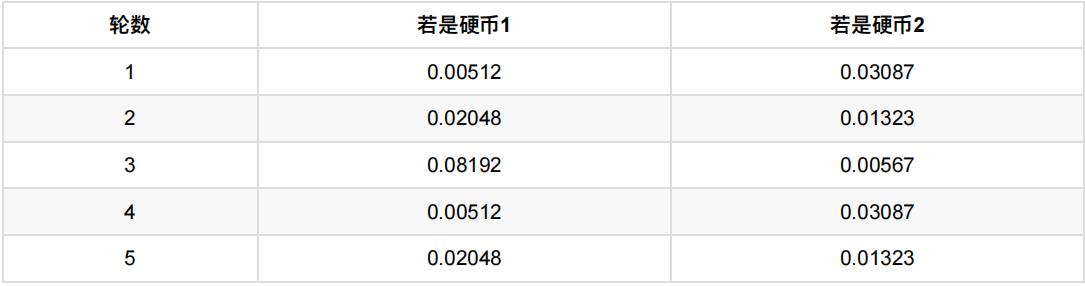
按照最⼤似然法则:
- 第1轮中最有可能的是硬币2
- 第2轮中最有可能的是硬币1
- 第3轮中最有可能的是硬币1
- 第4轮中最有可能的是硬币2
- 第5轮中最有可能的是硬币1
我们就把上面的值作为z的估计值。然后按照最大似然概率法则来估计新的P1和P2。
- P1 = (2+1+2)/15 = 0.33
- P2=(3+3)/10 = 0.6
设想我们是全知的神,知道每轮抛掷时的硬币就是如本⽂第001部分标示的那样,那么,P1和P2的最⼤似然估计就是 0.4和0.5(下⽂中将这两个值称为P1和P2的真实值)。那么对⽐下我们初始化的P1和P2和新估计出的P1和P2:

看到没?我们估计的P1和P2相⽐于它们的初始值,更接近它们的真实值了!
可以期待,我们继续按照上⾯的思路,⽤估计出的P1和P2再来估计z,再⽤z来估计新的P1和P2,反复迭代下去,就可 以最终得到P1 = 0.4,P2=0.5,此时⽆论怎样迭代,P1和P2的值都会保持0.4和0.5不变,于是乎,我们就找到了P1和 P2的最大似然估计。
这⾥有两个问题:
-
1、新估计出的P1和P2⼀定会更接近真实的P1和P2?
- 答案是:没错,⼀定会更接近真实的P1和P2,数学可以证明,但这超出了本⽂的主题,请参阅其他书籍或文章。
-
2、迭代⼀定会收敛到真实的P1和P2吗?
- 答案是:不⼀定,取决于P1和P2的初始化值,上⾯我们之所以能收敛到P1和P2,是因为我们幸运地找到了好的初始化值。
3.2.2 EM进阶版
下⾯,我们思考下,上⾯的⽅法还有没有改进的余地?
我们是⽤最⼤似然概率法则估计出的z值,然后再⽤z值按照最⼤似然概率法则估计新的P1和P2。也就是说,我们使用了⼀个最可能的z值,⽽不是所有可能的z值。
如果考虑所有可能的z值,对每⼀个z值都估计出⼀个新的P1和P2,将每⼀个z值概率大小作为权重,将所有新的P1和 P2分别加权相加,这样的P1和P2应该会更好⼀些。
所有的z值有多少个呢?
显然,有2^5 = 32种,需要我们进⾏32次估值?
不需要,我们可以⽤期望来简化运算。
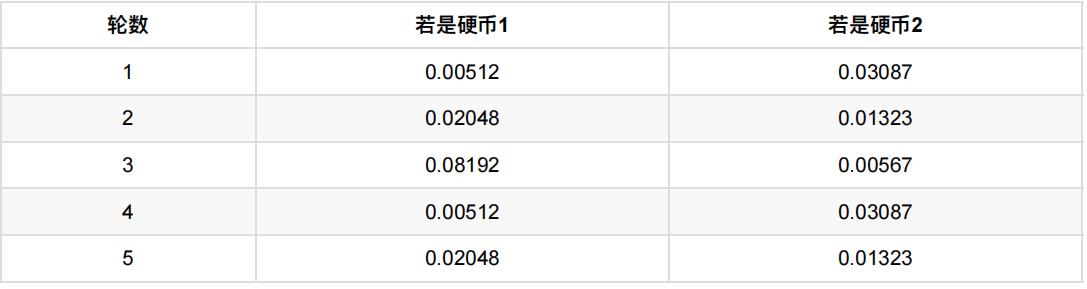
利⽤上⾯这个表,我们可以算出每轮抛掷中使⽤硬币1或者使⽤硬币2的概率。
⽐如第1轮,使⽤硬币1的概率是:
- 0.00512/(0.00512 + 0.03087) = 0.14
使⽤硬币2的概率是1-0.14=0.86
依次可以算出其他4轮的概率,如下:
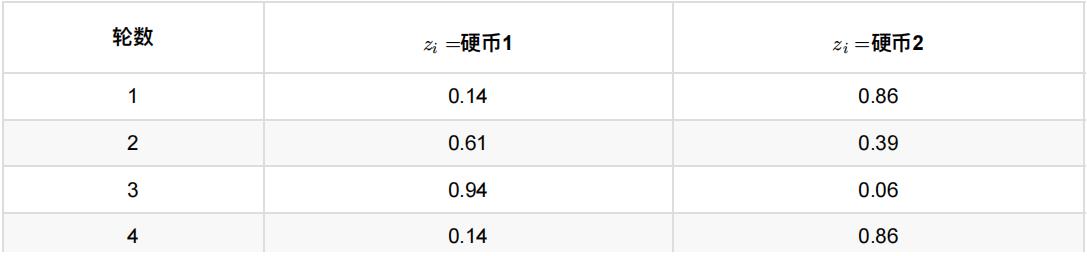

上表中的右两列表示期望值。看第⼀⾏,0.86表示,从期望的⻆度看,这轮抛掷使⽤硬币2的概率是0.86。相⽐于前⾯ 的⽅法,我们按照最⼤似然概率,直接将第1轮估计为⽤的硬币2,此时的我们更加谨慎,我们只说,有0.14的概率是硬 币1,有0.86的概率是硬币2,不再是⾮此即彼。这样我们在估计P1或者P2时,就可以⽤上全部的数据,⽽不是部分的 数据,显然这样会更好⼀些。
这⼀步,我们实际上是估计出了z的概率分布,这步被称作E步。
结合下表:
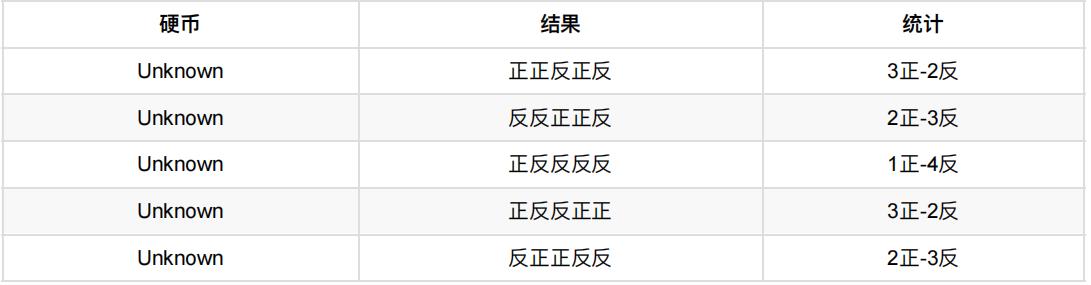
我们按照期望最⼤似然概率的法则来估计新的P1和P2:
以P1估计为例,第1轮的3正2反相当于
- 0.14*3=0.42正
- 0.14*2=0.28反
依次算出其他四轮,列表如下:
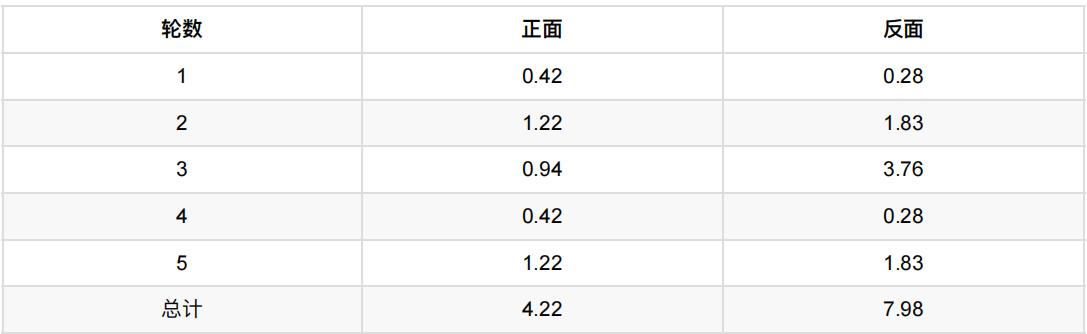
P1=4.22/(4.22+7.98)=0.35
可以看到,改变了z值的估计方法后,新估计出的P1要更加接近0.4。原因就是我们使⽤了所有抛掷的数据,而不是之前 只使⽤了部分的数据。
这步中,我们根据E步中求出的z的概率分布,依据最⼤似然概率法则去估计P1和P2,被称作M步。
3.3 小结
- EM算法的实现思路:
- ⾸先根据⼰经给出的观测数据,估计出模型参数的值;
- 然后再依据上⼀步估计出的参数值估计缺失数据的值,再根据估计出的缺失数据加上之前⼰经观测到的数据重 新再对参数值进⾏估计;
- 然后反复迭代,直⾄最后收敛,迭代结束。
加油!
感谢!
努力!
以上是关于机器学习EM算法的主要内容,如果未能解决你的问题,请参考以下文章
EM算法(Expectation Maximization Algorithm)详解(附代码)---大道至简之机器学习系列---通俗理解EM算法。