九大排序算法（C语言）

Posted 2021-08-26 是渣渣呀

九大排序算法

文章目录

• 九大排序算法
• • 直接插入排序（插入排序）
  • 折半插入排序（插入排序）
  • 希尔排序
  • 冒泡排序（交换排序）
  • 快速排序（交换排序）
  • 简单选择排序（选择排序）
  • 堆排序（选择排序）
  • 归并排序
  • 基数排序

直接插入排序（插入排序）

算法思想

算法思想：每次将⼀个待排序的记录按其关键字⼤⼩插⼊到前⾯已排好序的⼦序列中，直到全部记录插⼊完成。

算法实现

#include<stdio.h>
//升序排列（小-->大） 
void InsertSort(int A[],int n){
	int i,j,temp;
	for(i = 1; i < n; i++)
		if(A[i] < A[i-1]){ 
			temp = A[i];		//先将当前要插入的元素保存 
			for(j = i - 1; j >= 0 && A[j] > temp; j--)
				A[j+1] = A[j];	//将i前面比它大的元素依次后移一位 
			A[j+1] = temp;		//复制到插入位置 
		}
}
int main(){
	int A[10] = {32,21,55,32,23,42,87,57,91,23};
	printf("初始序列：");
	for(int i = 0; i < 10; i++)
		printf("%d ",A[i]);
	printf("\\n排序后序列：");
	InsertSort(A,10);
	for(int i = 0; i < 10; i++)
		printf("%d ",A[i]); 
} 

运行结果

效率分析

1. 最好情况：共n-1趟处理，每⼀趟只需要对⽐关键字1次，不⽤移动元素

   最好时间复杂度—— O(n)

2. 最坏情况：

   第1趟：对⽐关键字2次，移动元素3次

   第2趟：对⽐关键字3次，移动元素4次

   …

   第 i 趟：对⽐关键字 i+1次，移动元素 i+2 次

   第n-1趟：对⽐关键字 n 次，移动元素 n+1 次

   最坏时间复杂度——O(n^2)

3. 平均时间复杂度：O(n^2)

4. 算法稳定性：稳定

折半插入排序（插入排序）

算法思想

思路：先⽤折半查找找到应该插⼊的位置，再移动元素

算法实现

当 low>high 时折半查找停⽌，应将 [low, i-1] 内的元素全部右移，并将 A[0] 复制到 low 所指位置

当 A[mid]==A[0] 时，为了保证算法的“稳定性”，应继续在 mid 所指位置右边寻找插⼊位置

#include<stdio.h>
//升序排列（小-->大） 
void InsertSort(int A[],int n){
	int i,j,low,high,mid,temp;
	for(i = 1; i < n; i++){
		if(A[i] < A[i-1]){
			temp = A[i];		//先将当前要插入的元素保存 
			low = 0, high = i - 1;
			while(low <= high){	//折半查找（之前是有序序列） 
				mid = (low + high) / 2;
				if(A[mid] > temp) high = mid - 1;   //查找右半子表 
				else low = mid + 1;					//查找左半子表 
			}
			for(j = i - 1; j >= high + 1; j--)
				A[j+1] = A[j];	//将i前面比它大的元素依次后移一位
			A[high+1] = temp;		//复制到插入位置 
		}
	}
}
int main(){
	int A[10] = {32,21,55,32,23,42,87,57,91,23};
	printf("初始序列：");
	for(int i = 0; i < 10; i++)
		printf("%d ",A[i]);
	printf("\\n排序后序列：");
	InsertSort(A,10);
	for(int i = 0; i < 10; i++)
		printf("%d ",A[i]); 
} 

运行结果

效率分析

移动元素的次数变少了，但是关键字对⽐的次数依然是O(n^2) 数量级，整体来看时间复杂度依然是O(n^2)

希尔排序

算法思想

先追求表中元素部分有序，再逐渐逼近全局有序

希尔排序：先将待排序表分割成若⼲形如 L[i, i + d, i + 2d,…, i + kd] 的“特殊”⼦表，对各个⼦表分别进⾏直接插⼊排序。缩⼩增量d，重复上述过程，直到d=1为⽌。

算法实现

#include<stdio.h>
//升序排列（小-->大） 
void ShellSort(int A[],int n){
	int i,j,d,temp;
	for(d = n / 2; d >= 1; d /= 2)
		for(i = d; i < n; i++)		//从增量d的下标开始往后遍历 
			if(A[i] < A[i-d]){		//对每个元素所属的增量序列 进行直接插入排序 
				temp = A[i];
				for(j = i - d; j >= 0 && A[j] > temp; j-=d)
					A[j+d] = A[j];	//记录后移，查找插入的位置 
				A[j+d] = temp;		//插入 
			}
}
int main(){
	int A[10] = {32,21,55,32,23,42,87,57,91,23};
	printf("初始序列：");
	for(int i = 0; i < 10; i++)
		printf("%d ",A[i]);
	printf("\\n希尔排序后：");
	ShellSort(A,10);
	for(int i = 0; i < 10; i++)
		printf("%d ",A[i]); 
} 

运行结果

效率分析

1. 时间复杂度：和增量序列 d1, d2, d3… 的选择有关，⽬前⽆法⽤数学⼿段证明确切的时间复杂度 最坏时间复杂度为 O(n^2)，

   当n在某个范围内时，可达O(n^1.3)

2. 空间复杂度：O(1)

3. 稳定性：不稳定！

4. 适⽤性：仅适⽤于顺序表，不适⽤于链表

冒泡排序（交换排序）

算法思想

从后往前（或从前往后）两两⽐较相邻元素的值，若为逆序（即A[i-1]>A[i]），则交换它们，直到序

列⽐较完。称这样过程为“⼀趟”冒泡排序。

算法实现

#include<stdio.h>
//升序排列（小-->大） 
void BubbleSort(int A[],int n){
	int i,j,temp;
	for(i = 0; i < n - 1; i++){
		bool flag = false;			//标记本趟是否排序 
		for(j = n - 1; j > i; j--)	//一趟冒泡过程 
			if(A[j] < A[j-1]){		
				temp = A[j];		//交换 
				A[j] = A[j-1];
				A[j-1] = temp;
				flag = true;
			}		
		if(flag == false) return;	//本趟遍历后没有发生变化，说明表已经有序 
	}
}
int main(){
	int A[10] = {32,21,55,32,23,42,87,57,91,23};
	printf("初始序列：");
	for(int i = 0; i < 10; i++)
		printf("%d ",A[i]);
	printf("\\n排序后序列：");
	BubbleSort(A,10);
	for(int i = 0; i < 10; i++)
		printf("%d ",A[i]); 
} 

运行结果

效率分析

1. 空间复杂度：O(1)

2. 最好时间复杂度=O(n)-------⽐较次数=n-1；交换次数=0

3. 最坏时间复杂度=O(n^2)--------⽐较次数=(n-1)+(n-2)+…+1 = n(n-1) / 2 = 交换次数

4. 平均时间复杂度=O(n^2)

快速排序（交换排序）

算法思想

在待排序表L[1…n]中任取⼀个元素pivot作为枢轴（或基准，通常取⾸元素），通过⼀趟排序将待排序表划分为独⽴的两部分L[1…k-1]和L[k+1…n]，使得L[1…k-1]中的所有元素⼩于pivot，L[k+1…n]中的所有元素⼤于等于pivot，则pivot放在了其最终位置L(k)上，这个过程称为⼀次“划分”。然后分别递归地对两个⼦表重复上述过程，直⾄每部分内只有⼀个元素或空为⽌，即所有元素放在了其最终位置上。

算法实现

#include<stdio.h>
//升序排列（小-->大） 
int Partition(int A[],int low,int high){
	int pivot = A[low];		//一轮分区中把low位置的元素作为枢轴
	while(low < high){
		while(low < high && A[high] >= pivot) high--;	//从high往前找第一个小于枢轴的元素 
		A[low] = A[high];								//出来的一定是比枢轴小的，则放到low
		while(low < high && A[low] <= pivot) low++;		//从low往后找第一个大于枢轴的元素 
		A[high] = A[low];								//出来的一定是比枢轴大的，则放到high 
	} 
	A[low] = pivot;			//最终low的位置就是要枢轴元素的最终位置 
	return low;
}

void QuickSort(int A[],int low,int high){
	if(low < high){		//递归跳出的条件 
		int pivotpos = Partition(A,low,high);	//划分（可确定枢轴最终位置） 
		QuickSort(A,low,pivotpos-1);			//划分左子表 
		QuickSort(A,pivotpos+1,high);			//划分右子表
	}	
}

int main(){
	int A[10] = {32,21,55,32,23,42,87,57,91,23};
	printf("初始序列：");
	for(int i = 0; i < 10; i++)
		printf("%d ",A[i]);
	printf("\\n快速排序后：");
	QuickSort(A,0,9);
	for(int i = 0; i < 10; i++)
		printf("%d ",A[i]); 
} 

运行结果

效率分析

1. 时间复杂度=O(n*递归层数)

   最好时间复杂度=O(nlog2n)

   最坏时间复杂度=O(n2)

2. 空间复杂度=O(递归层数)

   最好空间复杂度=O(log2n)

   最坏空间复杂度=O(n)

3. 把n个元素组织成⼆叉树，⼆叉树的层数就是递归调⽤的层数n个结点的⼆叉树

   最⼩⾼度 = ⌊log2n⌋ + 1

   最⼤⾼度 = n

4. 稳定性：不稳定！

简单选择排序（选择排序）

算法思想

每⼀趟在待排序元素中选取关键字最⼩的元素加⼊有序⼦序列

算法实现

#include<stdio.h>
//升序排列（小-->大） 
void SelectSort(int A[],int n){
	int i,j,minIndex,temp;
	for(i = 0; i < n - 1; i++){
		minIndex = i; 				//记录最小元素位置 
		for(j = i + 1; j < n; j++)	
			if(A[j] < A[minIndex]) //只要找到比当前minIndex所指元素小的位置就更新minIndex 
				minIndex = j;
		if(minIndex != i){			//交换最小元素到 A[i] 
			temp = A[i]; 
			A[i] = A[minIndex];
			A[minIndex] = temp;
		}
	}
}
int main(){
	int A[10] = {32,21,55,32,23,42,87,57,91,23};
	printf("初始序列：");
	for(int i = 0; i < 10; i++)
		printf("%d ",A[i]);
	printf("\\n简单选择排序后：");
	SelectSort(A,10);
	for(int i = 0; i < 10; i++)
		printf("%d ",A[i]); 
} 

运行结果

效率分析

1. ⽆论有序、逆序、还是乱序，⼀定需要 n-1 趟处理 总共需要对⽐关键字 (n-1)+(n-2)+…+1 = n(n-1) / 2次

   元素交换次数 < n-1

2. 稳定性：不稳定

3. 适⽤性：既可以⽤于顺序表，也可⽤于链表

4. 空间复杂度：O(1)

5. 时间复杂度=O(n^2)

堆排序（选择排序）

完全二叉树的顺序存储

1. i 的左孩子 --2i

   i 的右孩子 --2i

   i 的父节点 – ⌊n/2⌋

   i 所在的层次 --log2(n + 1)或log2n向上取整 + 1

2. 若完全二叉树中共有n个结点，则

   判断 i 是否有左孩子？ --2i ≤ n ?

   判断 i 是否有右孩子？ --2i+1 ≤ n ?

   判断 i 是否是叶子/分支结点？-- i > ⌊n/2⌋ ?

堆的概念

若n个关键字序列L[1…n] 满⾜下⾯某⼀条性质，则称为堆（Heap）：

① 若满⾜：L(i)≥L(2i)且L(i)≥L(2i+1) （1 ≤ i ≤n/2）—— ⼤根堆（⼤顶堆）

② 若满⾜：L(i)≤L(2i)且L(i)≤L(2i+1) （1 ≤ i ≤n/2）—— ⼩根堆（⼩顶堆）

⼤根堆：完全⼆叉树中，根≥左、右

算法思想

1. 选择排序：每⼀趟在待排序元素中选取关键字最⼩（或最⼤）的元素加⼊有序⼦序列

2. 建立大（小）根堆

   1. 思路：把所有⾮终端结点都检查⼀遍，是否满⾜⼤（小）根堆的要求，如果不满⾜，则进⾏调整
   2. 在顺序存储的完全⼆叉树中，⾮终端结点编号 i≤⌊n/2⌋
   3. 检查当前结点是否满⾜ 根≥（≤）左、右 ，若不满⾜，将当前结点与更⼤（小）的⼀个孩⼦互换

3. 堆排序：每⼀趟将堆顶元素加⼊有序⼦序列 (与待排序序列中的最后⼀个元素交换）,

   并将待排序元素序列再次调整为⼤根堆（⼩元素不断“下坠”）

4. 注意：基于“大根堆”的堆排序得到“递增序列”，基于“⼩根堆”的堆排序得到“递减序列”

算法实现

注：根据树的顺序存储规则，要从下标为1的位置开始存储（这样才能通过下标找到孩子，父亲节点）, 代码中的0元素不参与排序！

#include<stdio.h>

//升序排列（小-->大） 
//将以 k 为子根的子树调整为大根堆（确定k的最终位置） 
void HeadAdjust(int A[],int k,int len){
	A[0] = A[k];						  //A[0]暂存子树的根节点 
	for(int i = 2*k; i <= len; i *= 2){   //沿key值较大的子节点向下筛选 
		if(i < len && A[i] < A[i+1])
			i++;						  //取左右孩子中key较大的孩子节点的下标 
		if(A[0] >= A[i]) break;			  //如果堆顶已经最大，该子树就满足大根堆了！ 
		else{
			A[k] = A[i];				  //将A[i]（较大的那个）调整到双亲节点上 
			k = i;					      //修改k值，以便继续筛选下面的子树节点 
		}
	}
	A[k] = A[0];						  //被筛选的节点值放入最终位置 
}

//建立大根堆 
void BuildMaxHeap(int A[],int len){
	for(int i = len/2;i > 0; i--){	 //从最后一个非终端（叶子）节点往前调整 
		HeadAdjust(A,i,len);
	}
}

void swap(int A[],int a,int b){
	int temp = A[a];
	A[a] = A[b];
	A[b] = temp;
}

void HeapSort(int A[],int len){
	BuildMaxHeap(A,len);			//初始建堆 
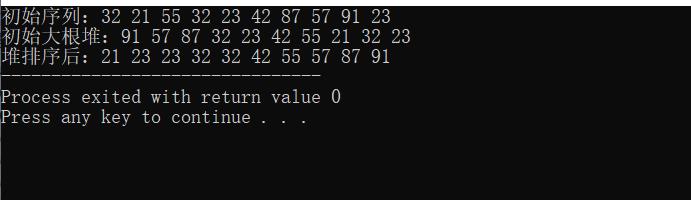
	printf("\\n初始大根堆：");
	for(int i = 1; i <= 10; i++)
		printf("%d ",A[i]); 
	for(int i = len;i > 1;i--){		//n-1趟的交换和建堆过程
		swap(A,i,1);				//堆顶元素和堆底元素交换（堆底用于存放有序序列） 
		HeadAdjust(A,1,i-1);		//把剩余的待排序元素整理成堆（注意剩余长度要减1） 
	}  	
}

int main(){
	int A[11] = {0,32,21,55,32,23,42,87,57,91,23};
	printf("初始序列：");
	for(int i = 1; i <= 10; i++)
		printf("%d ",A[i]);
	HeapSort(A,10);
	printf("\\n堆排序后：");
	for(int i = 1; i <= 10; i++)
		printf("%d ",A[i]); 
} 

运行结果

效率分析

1. 时间复杂度 = O(n) + O(nlog2n) = O(nlog2n)
2. 空间复杂度 = O(1)
3. 稳定性：不稳定！

归并排序

算法思想

归并：把两个或多个已经有序的序列合并成⼀个

算法实现

注：虽然归并和快速排序都是对数组递归排序，但处理左半部分、右半部分和处理当前层的顺序不同！！

​ 快速排序是在处理左和右半部分之前就要确定枢轴元素的最终位置，才能处理左右部分，所以一进递归就要处理当前层！

​ 归并排序是要把左右两部分有序块合并为一个有序块，则要先确定左右部分有序，所以对当前层的处理要在对左右部分处理之后进行！

#include<stdio.h>
#include<stdlib.h>
#define n 10
//辅助数组tmp
int *tmp = (int *)malloc(n*sizeof(int)); 

//升序排列（小-->大） 
void Merge(int A[],int low,int mid,int high){
	int i,j,k; 						// i：左半部分下界  j：右半部分下界  k：初始数组下标 
	for(k = low; k <= high; k++){
		tmp[k] = A[k];				//将A中所有元素复制到tmp中 
	}
	for(i = low,j = mid+1,k = i;i <= mid && j <= high;k++){ 
		if(tmp[i] < tmp[j])			//将较小值放入A中 
			A[k] = tmp[i++];
		else
			A[k] = tmp[j++];
	}
	while(i <= mid) A[k++] = tmp[i++];	//将左半部分剩余的元素放入A 
	while(j <= high) A[k++] = tmp[j++];	//将右半部分剩余的元素放入A
}

void MergeSort(int A[],int low,int high){
	if(low < high){		  
		int mid = (low + high) / 2;
		MergeSort(A,low,mid);			//划分左部分 
		MergeSort(A,mid + 1,high);			//划分右部分 
		Merge(A,low,mid,high);				//归并左右两个有序块 
	}	
}

int main(){
	int A[10] = {32,21,55,32,23,42,87,57,91,23};
	printf("初始序列：");
	for(int i = 0; i < 10; i++)
		printf("%d ",A[i]);
	printf("\\n归并排序后：");
	MergeSort(A,0,9);
	for(int i = 0; i < 10; i++)
		printf("%d ",A[i]); 
} 

运行结果

效率分析

2路归并的归并树——形态上就是⼀棵倒⽴的⼆叉树

⼆叉树的第h层最多有 2^(h−1) 个结点

若树⾼为h，则应满⾜ n ≤ 2^(h−1) , 即 h − 1 = ⌈log2n⌉

结论：

1. n个元素进⾏2路归并排序，归并趟数=⌈log2n⌉
2. 每趟归并时间复杂度 =O(n) ，则算法时间复杂度= O*(nlog2*n)
3. 空间复杂度 =O(n)，来⾃于辅助数组B

基数排序