九大排序算法（Python 语言实现）

Posted 2021-05-21 Amo Xiang

目录

• 一、选择排序法
• 二、冒泡排序法
• 三、直接插入排序法
• 四、合并排序法
• 五、希尔排序法
• 六、快速排序法
• 七、堆排序法
• • 7.1 树的概念
  • 7.2 树的表示
  • 7.3 树的相关术语
  • 7.4 什么是二叉树
  • 7.5 二叉树类别
  • 7.6 堆的概念
  • 7.7 使用堆进行排序
• 八、计数排序法
• 九、基数排序法
• 十、Python 各种排序算法的比较
• • 10.1 走进算法的世界
  • • 10.1.1 什么是算法
    • 10.1.2 算法的作用
    • 10.1.3 算法的基础
    • 10.1.4 大 O 表示法
  • 10.2 各种排序算法的比较

文章内容

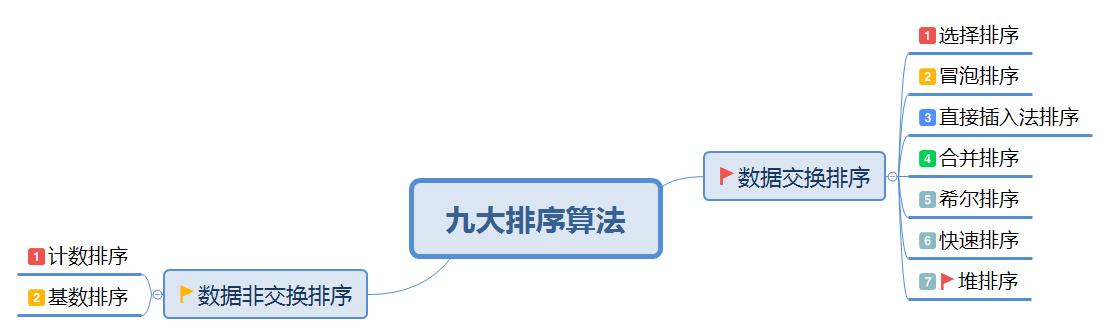
一、选择排序法

选择排序法就是反复从未排序的数列中取出最小(或最大)的数据，将其存放在序列的起始位置，然后，再从未排序的元素中继续寻找最小(或最大)的数据，存放在已排序序列的末尾，以此类推。最后的结果即为已排序好的数列。选择排序法最后的结果有两种形式，即递增数列和递减数列，下面就对于两种结果形式的具体排序流程进行描述。

1. 结果为递增排序：首先在未排序数列中取最小值，与数列第一个位置交换；然后再从未排序的数列中取最小值，与数列的第二个位置交换。如此重复，直到排序数列中的数据按照从小到大的顺序排序完成。
2. 结果为递减排序：首先在未排序数列中取最大值，与数列第一个位置交换；然后再从未排序的数列中取最大值，与数列的第二个位置交换。如此重复，直到排序数列中的数据按照从大到小的顺序排序完成。

接下来用一组数据来详细讲解选择排序法。例如，有这样一组数据：56，18，49，84，72，如下图所示：

按照递增顺序进行排序，步骤如下：

步骤1：找到所示数列中的最小值18与此数列中的第一个元素56交换，如下图所示：

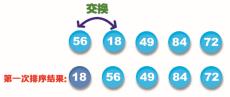
步骤2：从第二个值开始，找到此数列中（不包含第一个值）的最小值49，再和第二个值 56 交换，如下图所示：

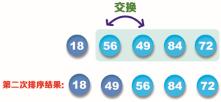
步骤3：从第三个值开始，找到此数列中（不包含第一、第二个值）的最小值56，由于它本来就是在第三个位置，故不需要进行交换。

步骤4：从第四个值开始，找到此数列中（不包含第一、第二、第三个值）的最小值72，再和第四个值84交换，如下图所示：

步骤5：数列递增顺序排序完毕，结果如下图所示：

【实例1】使用选择排序法进行递增排序。使用选择排序法为列表：56，18，49，84，72，进行递增排序。具体代码如下：

def choose(data, data_len):  # 自定义一个选择排序法函数
    for m in range(data_len - 1):  # 遍历新数据
        for n in range(m + 1, data_len):
            if data[n] < data[m]:  # 如果数据小于原来的数据
                data[m], data[n] = data[n], data[m]  # 需要交换位置
        print('第 %d 次排序之后的结果是' % (m + 1), end='')  # 提示
        for n in range(data_len):  # 遍历每次排序的结果
            print('%3d' % data[n], end='')  # 输出结果
        print()  # 输出空行


num_list = [56, 18, 49, 84, 72]  # 创建数列并初始化
length = len(num_list)
print("原始数据为：")  # 提示
for i in range(length):  # 遍历原有数据
    print('%3d' % num_list[i], end='')  # 输出结果
print('\\n---------------------------')  # 输出分界符
choose(num_list, length)  # 调用选择排序法函数
print('\\n---------------------------')  # 输出分界符
print("排序之后的数据为：")  # 提示
for j in range(length):  # 遍历排序好的新数列的数据
    print('%3d' % num_list[j], end='')  # 输出结果
print('')  # 输出空行

程序运行结果如下图所示：

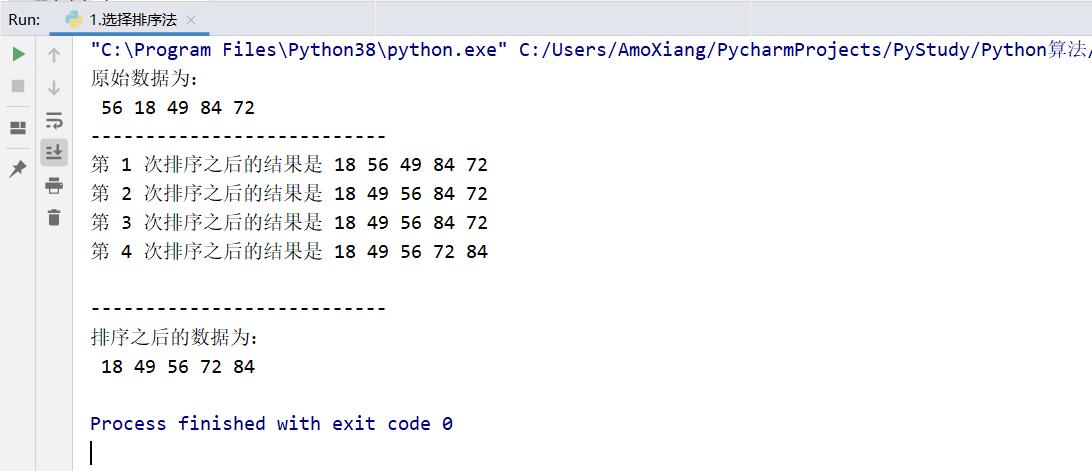
二、冒泡排序法

冒泡排序法是观察水中气泡变化而创造的排序方法，它的基本原理是从第一个数据开始，比较相邻数据的大小，如果大小顺序有误，则对调之后再与下一个数据进行比较，就像气泡逐渐从水底上升到水面上的情况。经过这样不断交换之后，就可以找出最后一个数据的正确位置。接着逐步进行交换，直到完成所有数据的排序为止。

冒泡排序法最后的结果也有两种形式，即递增数列和递减数列。接下来用一组数据来详细讲解冒泡排序法的基本原理。

例如，有这样一组数据：56、20、84、66、13，如下图所示：

按照递增顺序进行排序，步骤如下：

步骤1：首先用第一个位置的数据 56 与第二个位置的数据 20 进行比较，因为 20 小于 56，所以进行交换；然后再用第二个位置的数据 56 与第三个位置的数据 84 进行比较，因为 56 小于 84，所以不用交换；再用第三个位置的数据 84 与第四个位置的数据 66 进行比较，因为 66 小于 84，所以进行交换；最后用第四个位置的数据 84 与第五个位置的数据 13 进行比较，因为 84 大于 13，所以进行交换。这样就完成了第一次的排序，排序过程如下图所示：

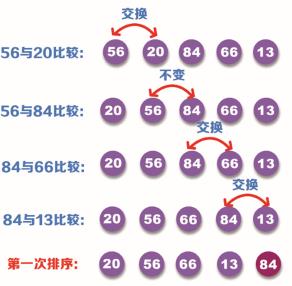
步骤2：经过第一次排序，已经将最大值 84 放在了对应的位置，因此在进行第二次排序时比较到 13 即可。

第二次排序依然从第一个位置开始比较，即比较数据 20 与 56 的大小，因为 20 小于 56，所以不需要交换；然后比较数据 56 与 66 的大小，因为 56 小于 66，所以不需要交换；最后比较数据 66 与 13 的大小，因为 66 大于 13，所以需要交换。这样就完成了第二次排序，排序过程如下图所示：

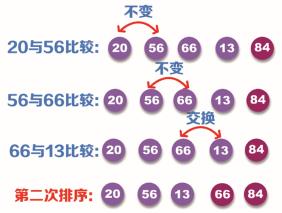
步骤3：经过第二次排序，已经将剩下数列 (除84以外) 的最大值 66 放在了对应的位置，因此在进行第三次排序时比较到 13 即可。

第三次排序依然从第一个位置开始进行比较，即比较数据 20 与 56 的大小，因为 20 小于 56，所以不需要交换位置；然后比较数据 56 与 13 的大小，因为 56 大于 13，所以需要交换位置。这样就完成了第三次排序，排序过程如下图所示：

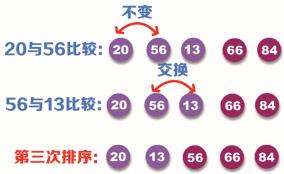
步骤4：经过第三次排序，已经将数列 84，66，56 放在了对应的位置，因此在进行第四次排序时比较到 13 即可。

第四次排序依然从第一个位置开始比较，比较数据 20 与 13 进行的大小，因为 20 大于 13，所以需要交换位置。这样就完成了第四次排序，排序过程如下图所示：

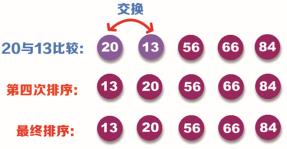
至此，排序完成。

【实例2】使用冒泡排序法进行递增排序。使用冒泡排序法为列表：56，20，84，66，13，进行递增排序。具体代码如下：

def bubble(data, data_len):  # 自定义一个冒泡排序法函数
    traversal_times = data_len - 1
    for m in range(traversal_times, 0, -1):  # 遍历排序次数
        for n in range(m):  # 遍历新数据
            if data[n + 1] < data[n]:  # 如果数据小于原来的数据
                data[n], data[n + 1] = data[n + 1], data[n]  # 需要交换位置
        print('第 %d 次排序之后的结果是' % (data_len - m), end='')  # 提示
        for n in range(data_len):  # 遍历每次排序的结果
            print('%3d' % data[n], end='')  # 输出结果
        print()  # 输出空行


num_list = [56, 20, 84, 66, 13]  # 创建数列并初始化
length = len(num_list)
print("原始数据为：")  # 提示
for i in range(length):  # 遍历原有数据
    print('%3d' % num_list[i], end='')  # 输出结果
print('\\n---------------------------')  # 输出分界符
bubble(num_list, length)  # 调用冒泡排序法函数
print('---------------------------')  # 输出分界符
print("排序之后的数据为：")  # 提示
for i in range(length):  # 遍历排序好的新数列的数据
    print('%3d' % num_list[i], end='')  # 输出结果
print('')  # 输出空行

程序运行结果如下图所示：

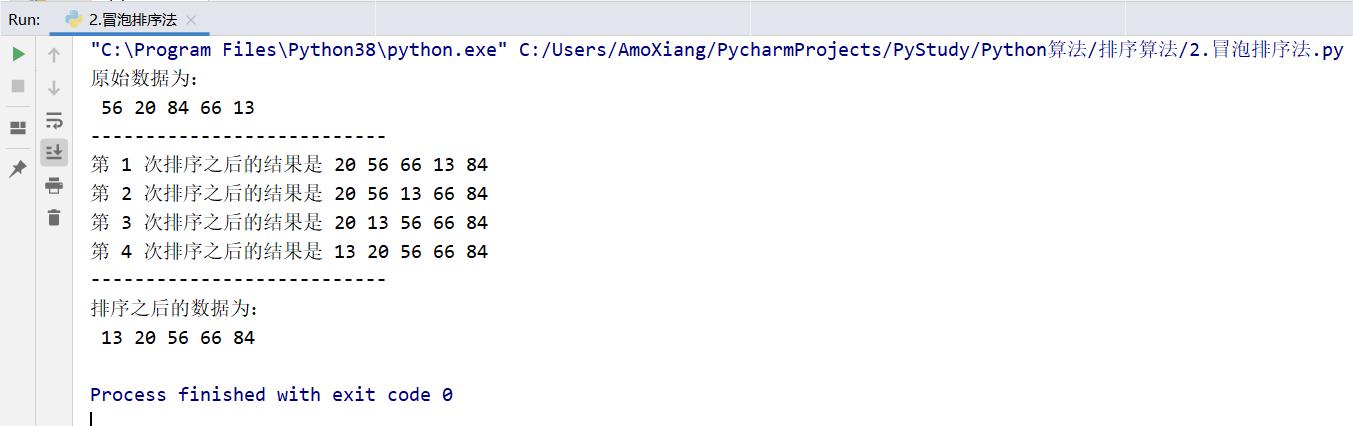
从上图所示的运行结果来看，排序的步骤和上述介绍的冒泡排序法步骤完全吻合。

【练习1】黄金档各个电视台综艺收视率排名。如今各个电视台在每周五的黄金档会有独播的综艺节目，某周的电视台黄金档综艺的收视率情况数据如下：14，27，28，04，21（省略其%），用冒泡排序法把此收视率按照从高到低的顺序排序，程序运行结果如下图所示：

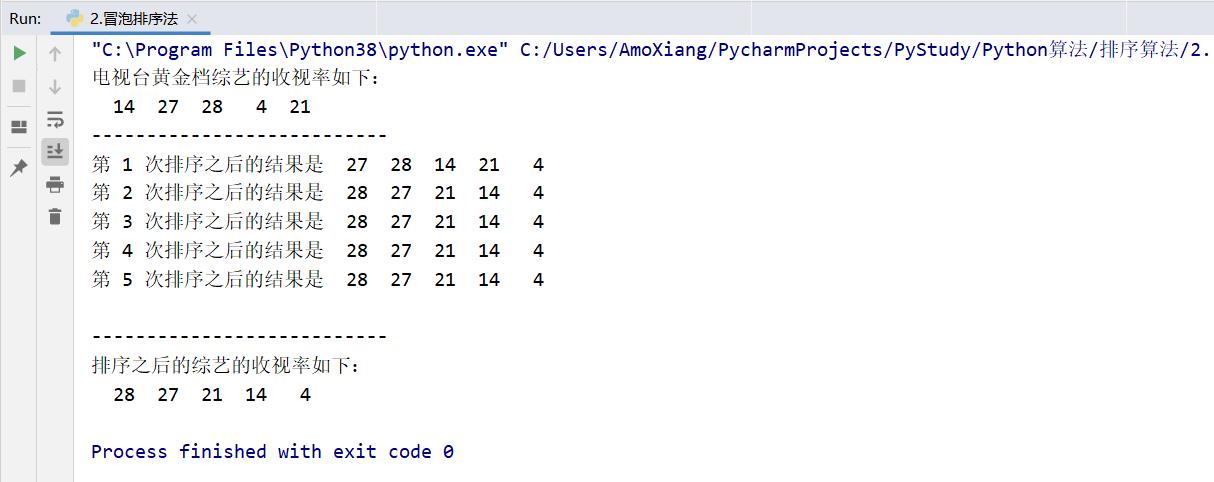
三、直接插入排序法

直接插入排序法是将数列中的数据，逐一与已排序好的数据进行比较。例如，在排好顺序的两个数据中插入第三个数据，就需要将其与排好的两个数据进行比较，通过比较结果将数据各自放在合适的位置。即在第三个数据插入数列时，这三个数据已然是排好顺序的。接着将第四个数据插入，以此类推，直到排序完成。

直接插入排序法最后的结果也有两种形式，即递增数列和递减数列。接下来通过一组数列具体来演示直接插入排序法的排序。例如，有这样一组数列：58，29，86，69，10，如下图所示：

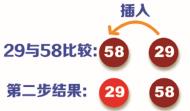
步骤3：将第三个位置上的数据 86 与 29 和 58 进行比较，因为 86 大于 29 和 58，所以直接将 86 放在第三个位置上，如下图所示：

步骤4：将第四个位置上的数据 69 与 29、58 和 86 进行比较，因为 69 大于 29 和 58，且 69 小于 86，所以直接将 69 插入到 86 前面的位置上，将 86 向后移一位，如下图所示：

步骤5：将第五个位置上的数据 10 分别与 29，58，69 和 86 进行比较，因为 10 小于 29，58，69 和 86，所以直接将 10 插入到 29 前面的位置上，将 29，58，69，86 依次向后移一位，如下图所示：

直接插入排序最终的排序结果如下图所示：

至此，排序完成。

【实例3】使用直接插入排序法进行递增排序。使用直接插入排序法对列表：58，29，86，69，10 进行递增排序。具体代码如下：

def insert(data):  # 自定义一个插入排序法函数
    for i in range(5):  # 遍历新数据
        temp = data[i]  # temp用来暂存数据
        j = i - 1
        # 循环排序，判断条件是数据的下标值要大于等于0且暂存数据小于原数据
        while j >= 0 and temp < data[j]:
            data[j + 1] = data[j]  # 把所有元素往后移一位
            j -= 1  # 下标减1
        data[j + 1] = temp  # 最小的数据插入最前一个位置
        print('第 %d 次排序之后的结果是' % (i + 1), end='')  # 提示
        for j in range(5):  # 遍历每次排序的结果
            print('%3d' % data[j], end='')  # 输出结果
        print()  # 输出空行


data = [58, 29, 86, 69, 10]  # 创建数列并初始化
print("原始数据为：")  # 提示
for i in range(5):  # 遍历原有数据
    print('%3d' % data[i], end='')  # 输出结果
print('\\n---------------------------')  # 输出分界符
insert(data)  # 调用直接插入排序法函数
print('\\n---------------------------')  # 输出分界符
print("排序之后的数据为：")  # 提示
for i in range(5):  # 遍历排序好的新数列的数据
    print('%3d' % data[i], end='')  # 输出结果
print('')  # 输出空行

程序运行结果如下图所示：

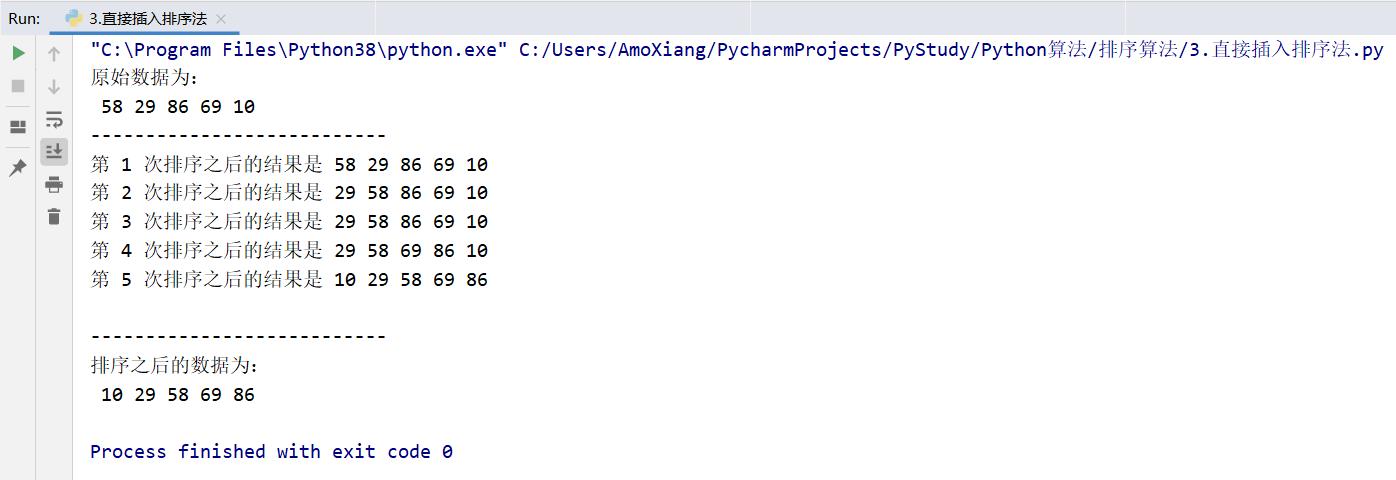
从上图所示的结果看，结果与上述介绍的直接插入排序法步骤完全吻合。

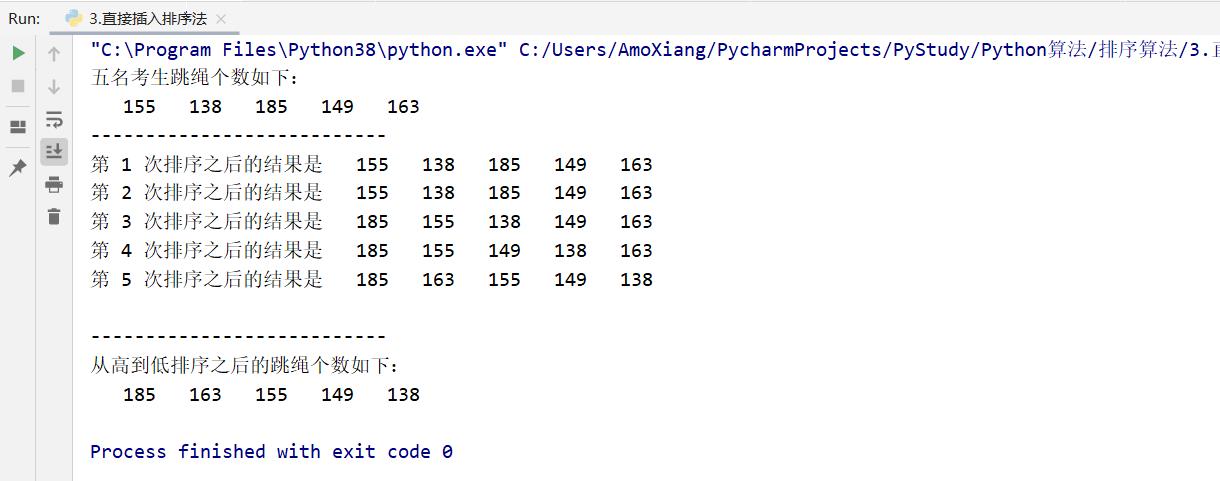
【练习2】输出跳绳成绩排名。身体是革命的本钱，体育锻炼是一件非常重要的事。因此，中考内容就加入了体育考试，跳绳就是其中一项考试内容。例如，某校中考的五名考生跳绳个数如下：155，138，185，149，163，利用直接插入法给这五位考生从高到低顺序排序，具体代码如下：

def insert(data):  # 自定义一个插入排序法函数
    for i in range(5):  # 遍历新数据
        temp = data[i]  # temp用来暂存数据
        j = i - 1
        # 循环排序，判断条件是数据的下标值要大于等于0且暂存数据大于原数据
        while j >= 0 and temp > data[j]:
            data[j + 1] = data[j]  # 把所有元素往后移一位
            j -= 1  # 下标减1
        data[j + 1] = temp  # 最小的数据插入最前一个位置
        print('第 %d 次排序之后的结果是' % (i + 1), end='')  # 提示
        for j in range(5):  # 遍历每次排序的结果
            print('%6d' % data[j], end='')  # 输出结果
        print()  # 输出空行


data = [155, 138, 185, 149, 163]  # 创建数列并初始化
print("五名考生跳绳个数如下：")  # 提示
for i in range(5):  # 遍历原有数据
    print('%6d' % data[i], end='')  # 输出结果
print('\\n---------------------------')  # 输出分界符
insert(data)  # 调用直接插入排序法函数
print('\\n---------------------------')  # 输出分界符
print("从高到低排序之后的跳绳个数如下：")  # 提示
for i in range(5):  # 遍历排序好的新数列的数据
    print('%6d' % data[i], end='')  # 输出结果
print('')

程序运行结果如下图所示：

四、合并排序法

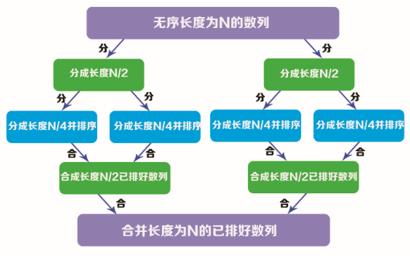
合并排序法是针对已经排序好的两个或两个以上的数列，通过合并的方式，将其组合成一个大的且排序好的数列。首先是将无序的数列分成若干小份，分若干份的规则就是 不断把每段长度除以2(对半分)，直到分到不能再分为止，然后对分好的数列进行排序，最后再逐步合并成一个排序好的大数列，如下图所示：

合并排序法最后的结果也有两种形式，即递增数列和递减数列。接下来通过一组数据来演示合并排序法的排序原理。例如，有这样一组数据：33，10，49，78，57，96，66，21，如下图所示：

按照递增进行排序，步骤如下：

步骤1：将原始数列一分为二，得到两个数列，即数列1和数列2，数列1为33，10，49，78；数列2为57，96，66，21，如下图所示：

步骤2：再分别将上图所示的数列1和数列2分别一分为二，得到数列a、数列b、数列c和数列d。此时每个数列中包含两个数据，并将每份中的两个数据进行排序，如下图所示：

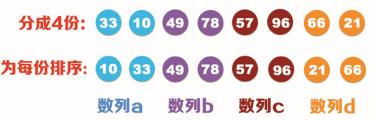
步骤3：将上图中排序好的数列元素进行合并，将数列a与数列b合并为数列A；将数列c与数列d合并为数列B。再对数列A和数列B中的数据元素进行排序，如下图所示：

步骤4：将上图中的数列A与数列B合并为一个数列，并将其内部的数据进行排序。最终的排序结果如下图所示：

至此，排序完成。

【实例4】使用合并排序法进行递增排序。使用合并排序法为列表：33，10，49，78，57，96，66，21进行排序。具体代码如下：

def merge_sort(data):  # 自定义合并排序法函数
    if len(data) <= 1:  # 判断列表元素是否小于或等于1
        return data  # 当列表元素只有一个的时候，直接返回
    mid = len(data) // 2  # 分隔长度计算，整个数据的长度除以2取整
    left = data[:mid]  # 左半边数据
    right = data[mid:]  # 右半边数据
    left = merge_sort(left)  # 调用merge_sort()函数继续对左半边分隔并排序
    right = merge_sort(right)  # 调用merge_sort()函数继续对右半边分隔并排序
    # 递归地进行排序
    result = []  # 用来存储结果值
    while left and right:  # 循环合并，判断条件是：左下标和右下标是否为真
        if left[0] <= right[0]:  # 判断左边数小于右边数
            result.append(left.pop(0))  # 结果增加left[0]的值
        else:
            result.append(right.pop(0))  # 结果增加right[0]的值
    if left:  # 如果left的值为真
        result += left  # 结果显示左侧数据
    if right:  # 如果right的值为真
        result += right  # 结果显示右侧数据
    return result  # 返回排序后的结果


data = [33, 10, 49, 78, 57, 96, 66, 21]  # 创建数列并初始化
print("原始数据为：", data)  # 输出原始数据
print('------------------------------------------------------')  # 输出分界符
print("排序之后的数据为：", merge_sort(data))  # 调用函数，输出排序好的数据
print('------------------------------------------------------')  # 输出分界符

程序运行结果如下图所示：

【练习3】“双十一”品牌手机销量排名。“双十一”是每年的购物狂欢节，参与的商家不尽其数，当然品牌手机也是“双十一”的热门销售商品之一。假设某五个品牌手机销售量（单位是万台）分别是：2750，3429，1632，4019，3698。利用合并排序法给销售量按照从高到低的顺序排序，具体代码如下：

def merge_sort(data):  # 自定义的合并排序法函数
    if len(data) <= 1:  # 判断列表元素是否小于或等于1
        return data  # 当列表元素只有一个的时候，直接返回
    mid = len(data) // 2  # 分隔长度计算，整个数据的长度除以2取整
    left = data[:mid]  # 左半边数据
    right = data[mid:]  # 右半边数据
    left = merge_sort(left)  # 调用merge_sort()函数继续对左半边分隔并排序
    right = merge_sort(right)  # 调用merge_sort()函数继续对右半边分隔并排序
    # 递归的进行排序
    result = []  # 用来存储结果值
    while left and right:  # 循环合并，判断条件是：左下标和右下标是否为真
        if left[0] >= right[0]:  # 判断左边数大于右边数
            result.append(left.pop(0))  # 结果增加left[0]的值
        else:
            result.append(right.pop(0))  # 结果增加right[0]的值
    if left:  # 如果left的值为真
        result += left  # 结果显示左侧数据
    if right:  # 如果right的值为真
        result += right  # 结果显示右侧数据
    return result  # 返回排序后的结果


data = [2750, 3429, 1632, 4019, 3698]  # 创建数列并初始化
print("五大品牌手机销售量如下：", data)  # 输出原始数据
print('＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝')  # 输出分界符
print("从高到低排序之后的销售量如下：", merge_sort(data))  # 调用函数，输出排序好的数据
print('＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝')  # 输出分界符

程序运行结果如下图所示：

五、希尔排序法

希尔排序法是插入排序法的一种，是直接插入排序算法的更高级的改进版本。希尔排序法可以减少插入排序法中数据移动的次数，加快排序的进行，因此它被称为缩小增量排序。希尔排序法排序的原则是将原始数据分成特定间隔的几组数据，然后使用插入排序法对每组数据进行排序，排序之后，再减小间隔距离，然后重复插入排序法对每组数据排序，直到所有数据完成排序为止。希尔排序法最后的结果有两种形式，即递增数列和递减数列。接下来通过一组数据来演示希尔排序法的排序原理。

例如，一组原始数据：60，82，17，35，52，73，54，9，如下图所示：

按照递增进行排序，步骤如下：

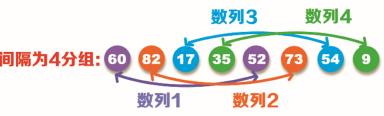
步骤1：从上图中可以看出，原始值中有 8 个数据，将间隔位数设置为 8/2=4，即将原始值分为四组数列，分别为：数列1（60，52）、数列2（82，73）、数列3（17，54）、数列4（35，9），如下图所示。将每个数列内的数据进行排序，按照左小右大的原则，将位置错误的数据进行交换，即数列1（52，60）、数列2（73，82）、数列3（17，54）和数列4（9，35）。

说明：间隔位数不一定必须除以 2，可以根据自己的需求而定。

步骤2：将步骤1排序后的数列进行插入放置，得出第一次排序结果，如下图所示：

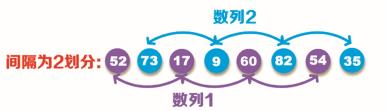
步骤3：接着缩小间隔[(8/2)/2=2]，即将原数列分为两组数列，分别为：数列1（52，17，60，54）、数列2（82，35，73，9），如下图所示，然后再对上图中的每个数列内的数据进行排序，按照从小到大的顺序，将位置错误的数据进行交换，即数列1（17，52，54，60）和数列2（9，35，73，82）。

步骤4：将步骤3排序后的数列进行插入放置，得出第二次排序结果，如下图所示：

步骤5：再以[（（8/2）/2）]2=1取间隔数，对第二次排序后的数列（如上图所示）中的每一个元素进行排序，得到最后的结果如下图所示：

至此，排序完成。

【实例5】使用希尔排序法进行递增排序。使用希尔排序法为列表：60，82，17，35，52，73，54，9进行递增排序。具体代码如下：

def hill(data):  C语言实现九大排序算法(建议收藏!)

 九大排序算法Java实现
 你需要知道的九大排序算法Python实现之快速排序
 你需要知道的九大排序算法Python实现之基数排序
 你需要知道的九大排序算法Python实现之堆排序
 九大排序算法（C语言）