Python小白的数学建模课-19.网络流优化问题

Posted youcans

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Python小白的数学建模课-19.网络流优化问题相关的知识，希望对你有一定的参考价值。


  • 流在生活中十分常见，例如交通系统中的人流、车流、物流，供水管网中的水流，金融系统中的现金流，网络中的信息流。网络流优化问题是基本的网络优化问题，应用非常广泛。
  • 网络流优化问题最重要的指标是边的成本和容量限制，既要考虑成本最低，又要满足容量限制，由此产生了网络最大流问题、最小费用流问题、最小费用最大流问题。
  • 本文基于 NetworkX 工具包，通过例程详细介绍网络最大流问题、最小费用流问题、最小费用最大流问题的建模和编程。
  • 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛达人。

1. 网络流优化

1.1 网络流

网络流优化问题是基本的网络优化问题，应用非常广泛，遍及通讯、运输、电力、工程规划、任务分派、设备更新以及计算机辅助设计等领域。

流从源点流出、通过路径输送、流入到汇点，从而将目标从源点输送到汇点。流在生活中十分常见，例如交通系统中的人流、车流、物流，供水管网中的水流，金融系统中的现金流，网络中的信息流。

现实中的任何路径都有最大流量（容量）的限制，在网络中也是如此，并以边的容量（Capacity）表示，一条边的流量不能超过它的容量。

把这些现实问题抽象为网络流问题，其特征是：（1）有向图上的每条边具有容量限制；（2）从源点流出的流量，等于汇点流入的流量；（3）源点和汇点之外的所有中间节点，流出的流量等于流入的流量。

注意在网络流问题中有几组概念容易混淆：

  • 源点/汇点，起点/终点，供应点/需求点：源点是只进不出的点，汇点是只出不进的点。源点/汇点 可以指定为问题的 起点/终点，但本质上源点/汇点是由网络结构特征决定的，而不是被指定的。供应点的供应量和需求点的需求量是固定/确定的，而源点/汇点的目标是发出/接收的流量最大，不是固定值。
  • 容量 与 流量：容量是路径（边、弧）允许的最大流通能力，用 c(i,j) 表示；流量则是路径（边、弧）上的实际流量，用 f(i,j) 表示。

1.2 典型的网络流优化问题

网络流优化问题最重要的指标是每条边的成本和容量限制，既要考虑成本最低（最短路径问题），又要满足容量限制（最大流问题），由此产生了网络最大流问题、最小费用流问题、最小费用最大流问题。

最大流问题（Maximun flow problem）：已知每条边的容量，研究如何充分利用网络能力，使从源点到汇点的总流量最大，也即在容量网络中求流量最大的可行流。

最小费用流问题（Minimum cost problem）：已知每条边的容量和单位流量的费用，对于给定的源点、汇点流量，研究如何分配流量和路径，使总费用最小，也即在容量费用网络中求成本最低的可行流。

最小费用最大流问题（Minimum cost maximum flow），已知每条边的容量和单位流量的费用，研究网络的流量最大的路径中，费用最小的路径。简单地说，就是满足最大流的路径可能有多条，需要从其中找到成本最低的路径。

Network 工具包求解网络流优化，包括最大流算法、最小割算法、最小费用流算法、最小费用最大流算法、容量缩放最小成本流算法。


2. 网络最大流问题（MFP）

2.1 网络最大流算法

网络最大流问题，是在容量网络 G(V,E) 中求流量 v(f) 达到最大的可行流 f。在最大流问题中，只能有一个源点和一个汇点。

求解网络最大流主要有增广路法和预流推进法两类方法。

增广路方法从一条可行流开始，用 BFS 或 DFS 从源到汇找到一条增广路，沿着该路径修改流量，不断重复这个过程，直到找不到增广路时停止，此时的流就是最大流。增广路方法有多种的实现算法，如 Ford Fulkerson 标号法的算法复杂度为 O ( E f ) O(E f) O(Ef)（不稳定），Edmonds Karp 算法的复杂度为 O ( V E 2 ) O(V E^2) O(VE2)，Dinic 算法的复杂度为 O ( V 2 E ) O(V^2 E) O(V2E)，ISAP 算法的复杂度也是 O ( V 2 E ) O(V^2 E) O(V2E)，但其速度是最快的。

预流推进方法也称压入与重标记方法，算法从源点开始向下推流，通过不断地寻找活结点，将流量推向以该点为起点的可推流边（压入过程）；如果在该点处找不到可推流边，则将该点的高度加 1，以实现将过大的流向后推进（重标记过程）。最高标号预流推进（HLPP）算法的复杂度为 O ( V 2 E ) O(V^2 E) O(V2E)，改进的 HLPP 算法的复杂度为 O ( V 2 ( E ) ) O(V^2 \\sqrt{(E)}) O(V2(E) ​)。


2.2 NetworkX 求解网络最大流问题

Network 工具包提供了多种求解网络最大流问题的算法和函数。其中 maximum_flow()、maximum_flow_value()、minimum_cut()、minimum_cut_value() 是集成了多种算法的通用函数，可以设置算法选项调用对应的算法；其它函数则是具体的算法实现函数。

函数功能
maximum_flow(flowG,s,t[, capacity,…])计算最大流
maximum_flow_value(flowG,s,t[,…])计算最大的单一目标流的值
minimum_cut(flowG,s,t[, capacity,flow_func])计算最小割的值和节点分区
minimum_cut_value(flowG,s,t[,capacity,…])计算最小割的值
edmonds_karp(G,s,t[,capacity,…])Edmonds-Karp 算法求最大流
shortest_augmenting_path(G,s,t[,…])SAP算法求最大流
dinitz(G,s,t[,capacity,…])Dinitz 算法求最大流
preflow_push(G,s,t[,capacity,…])HLPP 算法求最大流
boykov_kolmogorov(G,s,t[,capacity,…])Boykov-Kolmogorov 算法求最大流

2.3 maximum_flow() 函数说明

maximum_flow()、maximum_flow_value() 是求解网络最大流问题的通用方法，集成了多种算法可供选择。官网介绍详见：https://networkx.org/documentation/stable/reference/algorithms/flow.html 。

maximum_flow (flowG, _s, _t, capacity=‘capacity’, flow_func=None, *kwargs)
maximum_flow_value (flowG, _s, _t, capacity=‘capacity’, flow_func=None, *kwargs)

主要参数：

  • flowG(NetworkX graph)：有向图，边必须带有容量属性 capacity（不能用 ‘weight’ ）。
  • _s (node)：源点。
  • _t (node)：汇点。
  • capacity (string)：边的容量属性 capacity，缺省视为无限容量。
  • flow_func(function)：调用算法的函数名，如：‘edmonds_karp’, ‘shortest_augmenting_path’, ‘dinitz’, ‘preflow_push’, ‘boykov_kolmogorov’。缺省值 ‘None’ ，选择 ‘preflow_push’（HLPP 算法）。

返回值：

  • flow_value(integer, float)：网络最大流的流量值
  • flow_dict (dict)：字典类型，网络最大流的流经路径及各路径的分配流量

注意：如果要选择指定算法，需要写成以下形式 flow_func=nx.algorithms.flow.edmonds_karp，而不是 flow_func=edmonds_karp。也可以写成：

from networkx.algorithms.flow import edmonds_karp
flowValue, flowDict = nx.maximum_flow(G1, 's', 't', flow_func=edmonds_karp)

2.4 案例：输油管网的最大流量

问题描述：

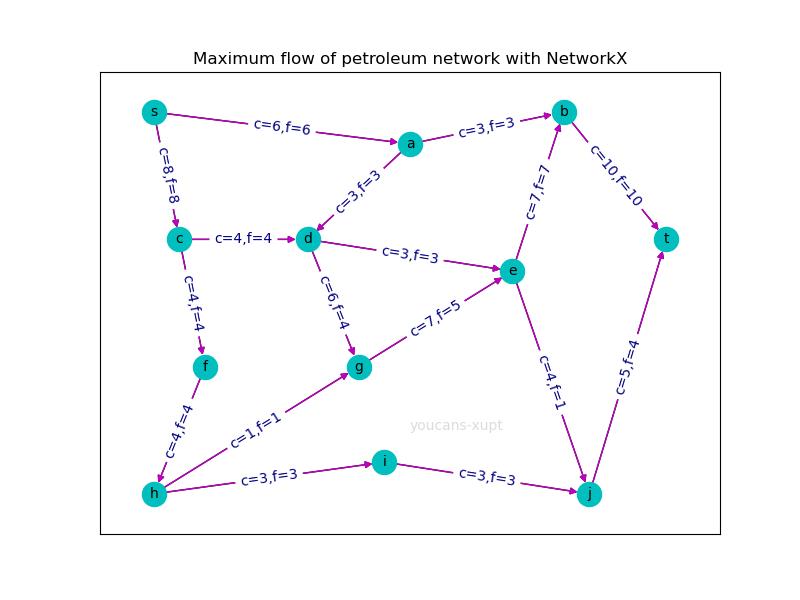
在输油管网中，通过输油管连接生产石油的油井、储存石油的油库和转运的中间泵站。各站点之间的连接及管路的容量如图（参见 2.6 程序运行结果图）所示，求从油井到油库的最大流量和具体方案。

问题分析：

这是一个网络最大流问题，可以用顶点表示油井、油库和泵站，其中油井为源点 s、油库为汇点 t，用有向边表示输油管，有向边的权 capacity 表示输油管的最大流量（容量）。

用 NetworkX 的 maximum_flow() 函数即可求出从从源点 s 到汇点 t 的最大流量。

程序说明：

  1. 图的输入。本例为稀疏有向图，使用 nx.DiGraph() 定义一个有向图。通过 add_edge(‘s’, ‘a’, capacity=6) 定义有向边和属性 capacity。注意必须以关键字 ‘capacity’ 表示容量，不能用权值 ‘weight’ 或其它关键字代替。

  2. nx.maximum_flow_value() 返回网络最大流的值，nx.maximum_flow() 可以同时返回网络最大流的值和网络最大流的路径及分配的流量。

  3. maxFlowDict 为字典类型，具体格式参加 2.6 程序运行结果。为了得到最大流所流经的边的列表edgeLists，要对 maxFlowDict 进行整理和格式转换。

  4. 在网络最大流图中，以边的标签显示了边的容量 c 和流量 f。


2.5 Python 例程

# mathmodel19_v1.py
# Demo19 of mathematical modeling algorithm
# Demo of network flow problem optimization with NetworkX
# Copyright 2021 YouCans, XUPT
# Crated：2021-07-15

import numpy as np
import matplotlib.pyplot as plt # 导入 Matplotlib 工具包
import networkx as nx  # 导入 NetworkX 工具包

# 1. 最大流问题 (Maximum Flow Problem，MFP)
# 创建有向图
G1 = nx.DiGraph()  # 创建一个有向图 DiGraph
G1.add_edge('s', 'a', capacity=6)  # 添加边的属性 "capacity"
G1.add_edge('s', 'c', capacity=8)
G1.add_edge('a', 'b', capacity=3)
G1.add_edge('a', 'd', capacity=3)
G1.add_edge('b', 't', capacity=10)
G1.add_edge('c', 'd', capacity=4)
G1.add_edge('c', 'f', capacity=4)
G1.add_edge('d', 'e', capacity=3)
G1.add_edge('d', 'g', capacity=6)
G1.add_edge('e', 'b', capacity=7)
G1.add_edge('e', 'j', capacity=4)
G1.add_edge('f', 'h', capacity=4)
G1.add_edge('g', 'e', capacity=7)
G1.add_edge('h', 'g', capacity=1)
G1.add_edge('h', 'i', capacity=3)
G1.add_edge('i', 'j', capacity=3)
G1.add_edge('j', 't', capacity=5)

# 求网络最大流
# maxFlowValue = nx.maximum_flow_value(G1, 's', 't')  # 求网络最大流的值
# maxFlowValue, maxFlowDict = nx.maximum_flow(G1, 's', 't')  # 求网络最大流
from networkx.algorithms.flow import edmonds_karp  # 导入 edmonds_karp 算法函数
maxFlowValue, maxFlowDict = nx.maximum_flow(G1, 's', 't', flow_func=edmonds_karp)  # 求网络最大流

# 数据格式转换
edgeCapacity = nx.get_edge_attributes(G1, 'capacity')
edgeLabel = {}  # 边的标签
for i in edgeCapacity.keys():  # 整理边的标签，用于绘图显示
    edgeLabel[i] = f'c={edgeCapacity[i]:}'  # 边的容量
edgeLists = []  # 最大流的边的 list
for i in maxFlowDict.keys():
    for j in maxFlowDict[i].keys():
        edgeLabel[(i, j)] += ',f=' + str(maxFlowDict[i][j])  # 取出每条边流量信息存入边显示值
        if maxFlowDict[i][j] > 0:  # 网络最大流的边（流量>0）
            edgeLists.append((i,j))

# 输出显示
print("最大流值: ", maxFlowValue)
print("最大流的途径及流量: ", maxFlowDict)  # 输出最大流的途径和各路径上的流量
print("最大流的路径：", edgeLists)  # 输出最大流的途径

# 绘制有向网络图
fig, ax = plt.subplots(figsize=(8, 6))
pos = {'s': (1, 8), 'a': (6, 7.5), 'b': (9, 8), 'c': (1.5, 6), 'd': (4, 6), 'e': (8, 5.5),  # 指定顶点绘图位置
       'f': (2, 4), 'g': (5, 4), 'h': (1, 2), 'i': (5.5, 2.5), 'j': (9.5, 2), 't': (11, 6)}
edge_labels = nx.get_edge_attributes(G1, 'capacity')
ax.set_title("Maximum flow of petroleum network with NetworkX")  # 设置标题
nx.draw(G1, pos, with_labels=True, node_color='c', node_size=300, font_size=10)  # 绘制有向图，显示顶点标签
nx.draw_networkx_edge_labels(G1, pos, edgeLabel, font_color='navy')  # 显示边的标签：'capacity' + maxFlow
nx.draw_networkx_edges(G1, pos, edgelist=edgeLists, edge_color='m')  # 设置指定边的颜色、宽度
plt.axis('on')  # Youcans@XUPT
plt.show()

2.6 程序运行结果

最大流值:  14
最大流的途径及流量:  {'s': {'a': 6, 'c': 8}, 'a': {'b': 3, 'd': 3}, 'c': {'d': 4, 'f': 4}, 'b': {'t': 10}, 'd': {'e': 3, 'g': 4}, 't': {}, 'f': {'h': 4}, 'e': {'b': 7, 'j': 1}, 'g': {'e': 5}, 'j': {'t': 4}, 'h': {'g': 1, 'i': 3}, 'i': {'j': 3}}
最大流的路径： [('s', 'a'), ('s', 'c'), ('a', 'b'), ('a', 'd'), ('c', 'd'), ('c', 'f'), ('b', 't'), ('d', 'e'), ('d', 'g'), ('f', 'h'), ('e', 'b'), ('e', 'j'), ('g', 'e'), ('j', 't'), ('h', 'g'), ('h', 'i'), ('i', 'j')]

在这里插入图片描述


3. 最小费用流问题（MCP）

3.1 最小费用流问题的算法

在实际问题中，我们总是希望在完成运输任务的同时，寻求运输费用最低的方案。最小费用流问题，就是要以最小费用从出发点（供应点）将一定的流量输送到接收点（需求点）。在最小流问题中，供应点、需求点的数量可以是一个或多个，但每个供应点的供应量和需求点的需求量是固定的。

最小费用流问题可以用如下的线性规划问题描述
KaTeX parse error: No such environment: align* at position 8: \\begin{̲a̲l̲i̲g̲n̲*̲}̲ & min\\;Cost=\\s…

求解最小费用流问题的方法很多，常见的如：连续最短路算法（Successive shortest path）、消圈算法（Cycle canceling）、原始对偶算法（Primal dual）、网络单纯性算法（Network simplex）和非均衡网络流算法（Out of Kilter法）等。

网络单纯形是单纯形算法的一个特殊应用，它使用生成树基来更有效地解决具有纯网络形式的线性规划问题。网络单纯性为最小费用流问题提供了标准的解决方法，可以解决数万个节点的大型问题。

最小费用流问题最重要的应用是配送网络的优化，如确定如何从出发地运送到中转站再转运到客户的配送方案。运输问题、指派问题、转运问题、最大流问题、最短路径问题，都是特殊情况下的最小费用流问题。例如，最短路径问题是流量 v=1 的最小费用流问题，最大流问题是最大流量下的最小费用流问题。只要选定合适的权重、容量、流量，解决最小费用流的方法就能用来解决上述问题。


3.2 NetworkX 求解最小费用流问题

Network 工具包提供了多个求解最小费用流问题的函数，所用的基本算法都是网络单纯性算法。

函数功能
network_simplex(G,[,demand,capacity,weight])单纯性法计算最小成本流
min_cost_flow_cost(G,[,demand,capacity,weight])计算最小成本流的成本
min_cost_flow(G,[,demand,capacity,weight])计算最小成本流
max_flow_min_cost(G,s,t[,capacity,weight])计算最小成本的最大流
capacity_scaling(G[,demand,capacity,…])计算容量缩放最小成本流

3.3 min_cost_flow() 函数说明

min_cost_flow()、min_cost_flow_cost() 是求解费用最小流问题的函数，通过调用网络单纯性算法函数 network_simplex() 求解。

min_cost_flow(G, demand=‘demand’, capacity=‘capacity’, weight=‘weight’)
min_cost_flow_cost(G, demand=‘demand’, capacity=‘capacity’, weight=‘weight’)

主要参数：

  • G(NetworkX graph)：有向图，边必须带有容量属性 capacity、单位成本属性 ‘weight’ 。
  • demand (string)：顶点的需求量属性 demand，表示节点的净流量：负数表示供应点的净流出量，正数表示需求点的净流入量，0 表示中转节点。缺省值为 0。
  • capacity (string)：边的容量，缺省视为无限容量。
  • weight (string)：边的单位流量的费用，缺省值为 0。

返回值：

  • flowDict (dict)：字典类型，最小费用流的流经路径及各路径的分配流量
  • flowCost(integer, float)：满足需求的最小费用流的总费用
  • NetworkXUnfeasible：输入的净流量(demand)不平衡，或没有满足需求流量的可行流时，抛出异常信息。

注意：费用最小流函数 min_cost_flow() 中并没有设定供应点、需求点，而是通过设置顶点属性 ‘demand’ 确定供应点、需求点及各顶点的净流量，因而允许网络中存在多个供应点、需求点。


3.4 案例：运输费用

问题描述：

从 s 将货物运送到 t。已知与 s、t 相连各道路的最大运输能力、单位运量的费用如图所示（参见 3.6 程序运行结果图），图中边上的参数 (9,4) 表示道路的容量为 9，单位流量的费用为 4。求流量 v 的最小费用流。

问题分析：

这是一个最小费用流问题。用 NetworkX 的 nx.min_cost_flow() 函数或 nx.network_simplex() 函数即可求出从供应点到需求点的给定流量 v 的最小费用流。

程序说明：

  1. 图的输入。本例为稀疏的有向图，使用 nx.DiGraph() 定义一个有向图，用G.add_weighted_edges_from() 函数以列表向图中添加多条赋权边，每个赋权边以元组 (node1,node2,{‘capacity’:c1, ‘weight’:w1}) 定义属性 ‘capacity’ 和 ‘weight’。注意必须以关键字 ‘capacity’ 表示容量，以 ‘weight’ 表示单位流量的费用。
  2. nx.shortest_path() 用于计算最短路径，该段不是必须的。将最短路径的计算结果与最小费用流的结果进行比较，可以看到流量 v=1 时最小费用流的结果与最短路径结果是相同的。
  3. nx.cost_of_flow() 用于计算最小费用最大流，该段不是必须的。将最小费用最大流的计算结果与最小费用流的结果进行比较，可以看到在最大流量 v=14 时最小费用流的结果与最小费用最大流结果是相同的。
  4. 最小费用流是基于确定的流量 v 而言的。流量 v 可以在程序中赋值；例程中 v 从 1 逐渐递增，计算所有流量下的最小费用流，直到达到网络容量的极限（如果再增大流量将会超出网络最大容量，没有可行流，计算最小费用流失败）。
  5. NetworkX 计算最小费用流时不是在函数中指定源点、汇点和流量，而是通过向源点、汇点添加属性 demand 实现的。demand 为正值时表示净输入流量，demand 为负值时表示净输出流量，这使我们可以指定多源多汇。
  6. nx.min_cost_flow() 返回最小费用流的路径和流量分配，字典格式；nx.min_cost_flow_cost() 返回最小费用流的费用值。nx.network_simplex() 也可以求最小费用流，返回最小费用流的费用值，路径和流量分配。
  7. 在最小费用流图中（最大流量 v=14），以边的标签显示了边的容量 c、单位流量的费用 w 和流量 f，如 (8,4),f=7 表示边的容量为 8，单位流量的费用为 4，分配流量为 7。
  8. 在最小费用流图中（最大流量 v=14），以不同颜色（edge_color=‘m’）和宽度（width=2）表示最小费用流的边，未使用的流量为 0 （f=0）的边以黑色绘制。

3.5 Python 例程：

# mathmodel19_v1.py
# Demo19 of mathematical modeling algorithm
# Demo of network flow problem optimization with NetworkX
# Copyright 2021 YouCans, XUPT
# Crated：2021-07-15

import numpy as np
import matplotlib.pyplot as plt # 导入 Matplotlib 工具包
import networkx as nx  # 导入 NetworkX 工具包

# 2. 最小费用流问题（Minimum Cost Flow，MCF）
# 创建有向图
G2 = nx.DiGraph()  # 创建一个有向图 DiGraph
G2.add_edges_from([('s','v1',{'capacity': 7, 'weight': 4}),
                  ('s','v2',{'capacity': 8, 'weight': 4}),
                  ('v1','v3',{'capacity': 9, 'weight': 1}),
                  ('v2','v1',{'capacity': 5, 'weight': 5}),
                  ('v2','v4',{'capacity': 9, 'weight': 4}),
                  ('v3','v4',{'capacity': 6, 'weight': 2}),
                  ('v3','t',{'capacity': 10, 'weight': 6}),
                  ('v4','v1',{'capacity': 2, 'weight': 1}),
                  ('v4','t',{'capacity': 5, 'weight': 2})]) # 添加边的属性 'capacity', 'weight'
# 整理边的标签，用于绘图显示
edgeLabel1 = nx.get_edge_attributes(G2, 'capacity')
edgeLabel2 &
以上是关于Python小白的数学建模课-19.网络流优化问题的主要内容，如果未能解决你的问题，请参考以下文章
 

 Python小白的数学建模课-21.关键路径法


 Python小白的数学建模课-A1.2021年数维杯C题（运动会优化比赛模式探索）探讨


 Python小白的数学建模课-12.非线性规划


 Python小白的数学建模课-12.非线性规划


 Python小白的数学建模课-A1.国赛赛题类型分析


 Python小白的数学建模课-A1.国赛赛题类型分析