Python小白的数学建模课-12.非线性规划
Posted youcans
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Python小白的数学建模课-12.非线性规划相关的知识,希望对你有一定的参考价值。
- 非线性规划是指目标函数或约束条件中包含非线性函数的规划问题,实际就是非线性最优化问题。
- 从线性规划到非线性规划,不仅是数学方法的差异,更是解决问题的思想方法的转变。
- 非线性规划问题没有统一的通用方法,我们在这里学习的当然不是数学方法,而是如何建模、如何编程求解。
- 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛达人。
1. 从线性规划到非线性规划
本系列的开篇我们介绍了线性规划 (Linear Programming) 并延伸到整数规划、0-1规划,以及相对复杂的固定费用问题、选址问题。这些问题的共同特点是,目标函数与约束条件都是线性函数。如果目标函数或约束条件中包含非线性函数,则是非线性规划。
通常,非线性问题都比线性问题复杂得多,困难得多,非线性规划也是这样。非线性规划没有统一的通用方法、算法来解决,各种方法都有特定的应用范围和适用条件。另一方面,很多非线性规划问题在实践中不能获得全局最优解,只能得到局部最优解或近似最优解。
这意味着什么?对于数学研究来说,这也许意味着存在新的课题和挑战,可以研究更有效的算法。确实如此,即便线性规划问题的研究也在不断前进,非线性规划问题的研究更是丰富多彩。但热闹是他们的,我什么也没有。
我所想到的,是数学建模学习/课程/竞赛的根本目的是什么?是掌握各种算法的推演,努力编程以实现,还是练习分析问题建立模型的能力,使用软件和工具求解问题的能力?显然是后者。可是,为什么培训课上老师讲的都是算法呢?到了例题例程,不是一带而过,就是跳步骤讲。听课时津津有味,下课了题目还是不会做,程序还是调不通。于是,…
不过,到了非线性规划这一课,我们发现老师也不再不厌其烦地讲算法了,不知道是讲不下去还是讲不过来了: 20世纪50年代,H.W.Kuhn 和 A.W.Tucker 提出了非线性规划的基本定理,为非线性规划奠定了理论基础 ;50、60 年代出现了许多解非线性规划问题的有效算法;80年代后,随着计算机技术的快速发展,非线性规划方法取得了长足进步,在信赖域法、稀疏拟牛顿法、并行计算、内点法和有限存储法等领域取得了丰硕的成果。
所以,没关系的,都一样——参见章北海文集。
这意味着什么呢?这意味着对于学习数学建模的小白,学会把问题简化为非线性规划的标准方程,学会按照本文的方法使用求解工具包的函数,才能求解非线性规划问题,才能完赛。
2. Scipy 库求解非线性规划问题
2.1 非线性规划问题的描述
首先,我们回顾线性规划问题的标准形式:
m i n f ( x ) = ∑ j = 1 n c j x j s . t . : { ∑ j = 1 n a i j x j = b i , x j ≥ 0 min\\;f(x) = \\sum_{j=1} ^n c_j x_j\\\\ s.t.:\\begin{cases} \\sum_{j=1} ^n a_{ij} x_j = b_i, \\\\ x_j \\geq 0 \\end{cases} minf(x)=j=1∑ncjxjs.t.:{∑j=1naijxj=bi,xj≥0
类似地,可以写出非线性规划的一般形式:
m i n f ( x ) s . t . : { h j ( x ) ≤ 0 , j = 1 , q g i ( x ) = 0 , i = 1 , p min\\;f(x) \\\\ s.t.:\\begin{cases} h_j(x) \\leq 0, &j=1,q\\\\ g_i(x) = 0, &i=1,p \\end{cases} minf(x)s.t.:{hj(x)≤0,gi(x)=0,j=1,qi=1,p
其中: x = [ x 1 , . . . , x n ] T x=[x_1,...,x_n]^T x=[x1,...,xn]T 为决策变量, f ( x ) f(x) f(x) 为目标函数, h j ( x ) h_j(x) hj(x) 和 g i ( x ) g_i(x) gi(x) 为约束条件。
由此可见,非线性规划问题,实际上就是带有约束条件的非线性函数优化问题。
按照我们的学习模式,非线性规划问题的建模和求解与线性规划问题是类似的,按照以下步骤进行:
- 问题定义,确定决策变量、目标函数和约束条件;
- 模型构建,由问题描述建立数学方程,并转化为标准形式的数学模型;
- 模型求解,用标准模型的优化算法对模型求解,得到优化结果。
2.2 Scipy 求解非线性规划问题的函数
Scipy 是 Python 算法库和数学工具包,包括最优化、线性代数、积分、插值、特殊函数、傅里叶变换、信号和图像处理、常微分方程求解等模块。
本文推荐和讲解使用 Scipy 工具包中的 optimize 模块求解常见的非线性规划问题。
scipy.optimize 模块中提供了多个用于非线性规划问题的方法,适用于不同类型的问题。
-
brent():单变量无约束优化问题,混合使用牛顿法/二分法。
-
fmin():多变量无约束优化问题,使用单纯性法,只需要利用函数值,不需要函数的导数或二阶导数。
-
leatsq():非线性最小二乘问题,用于求解非线性最小二乘拟合问题。
-
minimize():约束优化问题,使用拉格朗日乘子法将约束优化转化为无约束优化问题。
2.3 scipy.optimize.brent() 求解单变量无约束优化问题
非线性规划最简单的形式是一维搜索,一维搜索的常用方法是函数逼近法和区间收缩法。
brent() 函数是 SciPy.optimize 模块中求解单变量无约束优化问题最小值的首选方法。这是牛顿法和二分法的混合方法,既能保证稳定性又能快速收敛。
scipy.optimize.brent(func, args=(), brack=None, tol=1.48e-08, full_output=0, maxiter=500)
optimize.brent() 的主要参数:
- *func: callable f(x,args) 目标函数 f ( x ) f(x) f(x),以函数形式表示,可以通过 *args 传递参数
- args: tuple 可选项,以 f(x,*args) 的形式将可变参数 p 传递给目标函数 f ( x , p ) f(x,p) f(x,p) 。
- brack: tuple 可选项,搜索算法的开始区间(不是指 x 的上下限)
optimize.brent() 的主要返回值:
- **xmin: ** 返回函数达到最小值时的 x(注意是局部最优,不一定是全局最优)。
- **fval: ** 返回函数的最优值(默认不返回,仅当 full_output 为 1 时返回)。
optimize.brent() 的使用例程:
from scipy.optimize import brent, fmin_ncg, minimize
import numpy as np
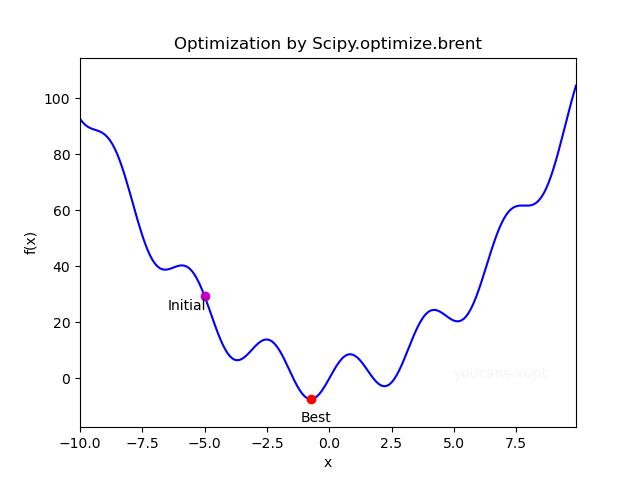
# 1. Demo1:单变量无约束优化问题(Scipy.optimize.brent)
def objf(x): # 目标函数
fx = x**2 - 8*np.sin(2*x+np.pi)
return fx
xIni = -5.0
xOpt= brent(objf, brack=(xIni,2))
print("xIni={:.4f}\\tfxIni={:.4f}".format(xIni,objf(xIni))
print("xOpt={:.4f}\\tfxOpt={:.4f}".format(xOpt,objf(xOpt)))
例程运行结果:
xIni=-5.0000 fxIni=29.3522
xOpt=-0.7391 fxOpt=-7.4195
2.4 scipy.optimize.fmin() 求解多变量无约束优化问题
多变量无约束优化问题的算法很多,分类方式也很多。从使用者的角度来说可以分为:只使用目标函数值、使用导数(梯度下降法)、使用二阶导数。大体来说,使用导数的算法收敛较快,使用二阶导数收敛更快,但是收敛快也容易陷入局部最优。
fmin() 函数是 SciPy.optimize 模块中求解多变量无约束优化问题(最小值)的首选方法,采用下山单纯性方法。下山单纯性方法又称 Nelder-Mead 法,只使用目标函数值,不需要导数或二阶导数值,是最重要的多维无约束优化问题数值方法之一。
scipy.optimize.fmin(func, x0, args=(), xtol=0.0001, ftol=0.0001, maxiter=None, maxfun=None, full_output=0, disp=1, retall=0, callback=None, initial_simplex=None)
optimize.fmin() 的主要参数:
- *func: callable f(x,args) 目标函数 f ( x ) f(x) f(x),以函数形式表示,可以通过 *args 传递参数。
- x0: nadarray 搜索算法的初值。
- args: tuple 可选项,以 f(x,*args) 的形式将可变参数 p 传递给目标函数 f ( x , p ) f(x,p) f(x,p) 。
optimize.fmin() 的主要返回值:
- **xopt: ** 返回最小值时的 x 值。
- **fopt: ** 返回最小值时的目标函数值,fopt=func(xopt)。
optimize.fmin() 的使用例程:
from scipy.optimize import brent, fmin, minimize
import numpy as np
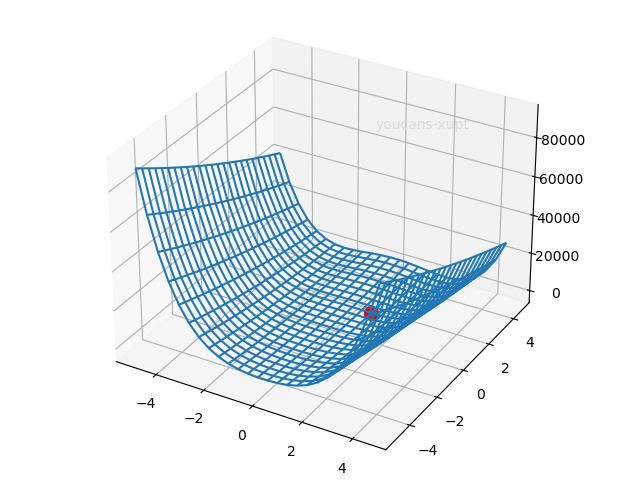
# 2. Demo2:多变量无约束优化问题(Scipy.optimize.brent)
# Rosenbrock 测试函数
def objf2(x): # Rosenbrock benchmark function
fx = sum(100.0 * (x[1:] - x[:-1] ** 2.0) ** 2.0 + (1 - x[:-1]) ** 2.0)
return fx
xIni = np.array([-2, -2])
xOpt = fmin(objf2, xIni)
print("xIni={:.4f},{:.4f}\\tfxIni={:.4f}".format(xIni[0],xIni[1],objf2(xIni)))
print("xOpt={:.4f},{:.4f}\\tfxOpt={:.4f}".format(xOpt[0],xOpt[1],objf2(xOpt)))
例程运行结果:
xIni=-2.0000,-2.0000 fxIni=3609.0000
xOpt=1.0000,1.0000 fxOpt=0.0000
3. scipy.optimize.minimize() 求解非线性规划问题
3.1 scipy.optimize.minimize() 函数说明
minimize() 函数是 SciPy.optimize 模块中求解多变量优化问题的通用方法,可以调用多种算法,支持约束优化和无约束优化。
scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)
optimize.minimize() 的主要参数:
- *fun: callable f(x,args) 目标函数 f ( x ) f(x) f(x),以函数形式表示,可以通过 *args 传递参数。
- x0: nadarray, shape(n,) 搜索算法的初值,n 是决策变量个数。
- args: tuple 可选项,将可变参数传递给目标函数 fun、导数函数 jac 和二阶导数函数 hess。
- method: str 可选项,选择优化算法。默认算法为 BFGS, L-BFGS-B, SLSQP(取决于问题有没有边界条件和约束条件)
- **jac: ** 可选项,梯度计算方法。可以以函数形式表示,或选择 ‘2-point’, ‘3-point’, ‘cs’。该选项只能用于 CG, BFGS, Newton-CG, L-BFGS-B, TNC, SLSQP, dogleg, trust-ncg, trust-krylov, trust-exact 和 trust-constr 算法。
- **hess: ** 可选项,Hessian 矩阵计算方法。可以以函数形式表示,或选择 ‘2-point’, ‘3-point’, ‘cs’。该选项只能用于 Newton-CG, dogleg, trust-ncg, trust-krylov, trust-exact 和 trust-constr 算法。
- **bounds: ** 可选项,变量的边界条件(上下限,lb<=x<=ub)。该选项只能用于 Nelder-Mead, L-BFGS-B, TNC, SLSQP, Powell 和 trust-constr 算法。
- **constraints: ** 可选项,定义约束条件 f(x)>=0。该选项只能用于 COBYLA, SLSQP 和 trust-constr 算法,注意不同算法中对于约束条件的定义是不同的。
optimize.minimize() 的主要返回值:
- **res: ** 返回优化结果,以对象方式表示,主要包括优化是否成功、决策变量的优化值 xOpt。
optimize.minimize() 的优化算法选项:
optimize.minimize() 的默认算法为 BFGS, L-BFGS-B, SLSQP(取决于问题有没有边界条件和约束条件),可以通过 “method=None” 选项调用多种算法:
无约束问题优化算法
-
**method=‘CG’ **: 非线性共轭梯度算法,只能处理无约束优化问题,需要使用一阶导数函数。
-
**method=‘BFGS’ **: BFGS 拟牛顿法,只能处理无约束优化问题,需要使用一阶导数函数。BFGS 算法性能良好,是无约束优化问题的默认算法。
-
**method=‘Newton-CG’ **: 截断牛顿法,只能处理无约束优化问题,需要使用一阶导数函数,适合处理大规模问题。
-
**method=‘dogleg’ **: dog-leg 信赖域算法,需要使用梯度和 Hessian(必须正定),只能处理无约束优化问题,
-
**method=‘trust-ncg’ **: 采用牛顿共轭梯度信赖域算法,需要使用梯度和 Hessian(必须正定),只能处理无约束优化问题,适合大规模问题。
-
method=‘trust-exact’: 求解无约束极小化问题的信赖域方法,需要梯度和Hessian(不需要正定)。
-
method=‘trust-krylov’: 使用Newton-GLTR 信赖域算法度,需要使用梯度和 Hessian(必须正定),只能处理无约束优化问题,适合中大规模问题。
边界约束条件问题优化算法
-
method=‘Nelder-Mead’: 下山单纯性法,可以处理边界约束条件(决策变量的上下限),只使用目标函数,不使用导数函数、二阶导数,鲁棒性强。
-
**method=‘L-BFGS-B’ **: 改进的 BFGS 拟牛顿法,L- 指有限内存,-B 指边界约束,可以处理边界约束条件,需要使用一阶导数函数。L-BFGS_B 算法性能良好,消耗内存量很小,适合处理大规模问题,是边界约束优化问题的默认算法。
-
method=‘Powell’: 改进的共轭方向法,可以处理边界约束条件(决策变量的上下限)。
-
**method=‘TNC’ **: 截断牛顿法,可以处理边界约束条件
带有约束条件问题优化算法
-
**method=‘COBYLA’ **: 线性近似约束优化方法,通过对目标函数和约束条件的线性逼近处理非线性问题。只使用目标函数,不需要导数或二阶导数值,可以处理约束条件。
-
**method=‘SLSQP’ **: 序贯最小二乘规划算法,可以处理边界约束、等式约束和不等式约束条件。SLSQP 算法性能良好,是带有约束条件优化问题的默认算法。
-
**method=‘trust-constr’ **: 信赖域算法,通用的约束最优化方法,适合处理大规模问题。
由于 optimize.minimize() 实际是多种算法的集成接口,各种算法对于问题、约束条件和参数的定义并不完全相同,对于各种算法的研究和应用已超出本文的内容,有兴趣的读者可以阅读官方文档: scipy.optimize.minimize — SciPy v1.7.0 Manual
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html#scipy.optimize.minimize
我们还是针对数学建模的常用需求和小白的特点,结合实际案例来学习基本应用。
3.2 scipy.optimize.minimize() 函数使用例程
编程步骤说明:
- 导入 scipy、numpy 包;
- 定义目标函数 objf3(x),输入变量 x 表示向量,返回值 fx 是目标函数的计算结果 。
- 定义边界约束,即优化变量的上下限:
- minimize() 默认无边界约束条件,即各自变量的取值范围没有限制;
- 如果设置边界约束,要对每个自变量(决策变量)定义其上下限,注意定义边界约束的格式;
- 如果某个自变量没有上限(下限),则表示为 None 。
- 定义 x 的初值。
- 求解最小化问题 resRosen,其中目标函数 objf3 和搜索的初值点 xIni 是必需的,指定优化方法和边界条件是可选项。如果优化问题是求最大值 maxFx,可以通过 minFx = - maxFx 的变换来实现。
- 通过调用最小化问题的返回值 resRosen.x 得到最优点 xOpt。
Python 例程:
from scipy.optimize import brent, fmin, minimize
import numpy as np
# 3. Demo3:多变量边界约束优化问题(Scipy.optimize.minimize)
# 定义目标函数
def objf3(x): # Rosenbrock 测试函数
fx = sum(100.0 * (x[1:] - x[:-1] ** 2.0) ** 2.0 + (1 - x[:-1]) ** 2.0)
return fx
# 定义边界约束(优化变量的上下限)
b0 = (0.0, None) # 0.0 <= x[0] <= Inf
b1 = (0.0, 10.0) # 0.0 <= x[1] <= 10.0
b2 = (-5.0, 100.) # -5.0 <= x[2] <= 100.0
bnds = (b0, b1, b2) # 边界约束
# 优化计算
xIni = np.array([1., 2., 3.])
resRosen = minimize(objf3, xIni, method='SLSQP', bounds=bnds)
xOpt = resRosen.x
print("xOpt = {:.4f}, {:.4f}, {:.4f}".format(xOpt[0],xOpt[1],xOpt[2]))
print("min f(x) = {:.4f}".format(objf3(xOpt)))
例程运行结果:
xOpt = 1.0000, 1.0000, 1.0000
min f(x) = 0.0000
4. 约束非线性规划问题实例
4.1 非线性规划问题的数学模型:
KaTeX parse error: No such environment: align at position 8: \\begin{̲a̲l̲i̲g̲n̲}̲ & min\\;f(x) = …
由于 minimize() 函数中对约束条件的形式定义为 f(x)>=0,因此要将问题的数学模型转换为标准形式:
KaTeX parse error: No such environment: align at position 8: \\begin{̲a̲l̲i̲g̲n̲}̲ & min\\;f(x) = …
4.2 Python 例程 1:
程序说明:
- 在本例程中,目标函数中的参数 a, b, c, d 在子程序中直接赋值,这种实现方式最简单;
- 定义边界约束,即优化变量的上下限,与 3.2 中的例程相同,用 minimize() 函数中的选项 bounds=bnds 进行定义。
- 定义约束条件:
- 本案例有 4个约束条件,2个等式约束、2个不等式约束,上节中已写成标准形式;
- 本例程将每个约束条件作为一个子函数定义,
- minimize() 函数对约束条件按照字典格式: {‘type’: ‘ineq’, ‘fun’: functionname} 进行定义。‘type’ 的键值可选 ‘eq’ 和 ‘ineq’,分别表示的是约束和不等式约束;functionname是定义约束条件的函数名。
- 求解最小化问题 res,其中目标函数 objF4 和搜索的初值点 x0 是必需的,指定优化方法和边界条件、约束条件是可选项。
- 通过调用最小化问题的返回值可以得到优化是否成功的说明(res.message)、自变量的优化值(res.x)和目标函数的优化值(res.fun)。
Python 例程:
from scipy.optimize import brent, fmin, minimize
import numpy as np
# 4. Demo4:约束非线性规划问题(Scipy.optimize.minimize)<以上是关于Python小白的数学建模课-12.非线性规划的主要内容,如果未能解决你的问题,请参考以下文章