Leetcode No.60 排列序列

Posted 2021-08-14 AI算法攻城狮

一、题目描述

给出集合 [1,2,3,...,n]，其所有元素共有 n! 种排列。

按大小顺序列出所有排列情况，并一一标记，当 n = 3 时, 所有排列如下：

"123"
"132"
"213"
"231"
"312"
"321"
给定 n 和 k，返回第 k 个排列。

示例 1：

输入：n = 3, k = 3
输出："213"

示例 2：

输入：n = 4, k = 9
输出："2314"

示例 3：

输入：n = 3, k = 1
输出："123"
 

提示：

1 <= n <= 9
1 <= k <= n!

二、解题思路

通过 计算剩余数字个数的阶乘数，一位一位选出第 k 个排列的数位。

容易想到，使用同「力扣」第 46 题： 全排列 的回溯搜索算法，依次得到全排列，输出第 k 个全排列即可。事实上，我们不必求出所有的全排列。

基于以下几点考虑：

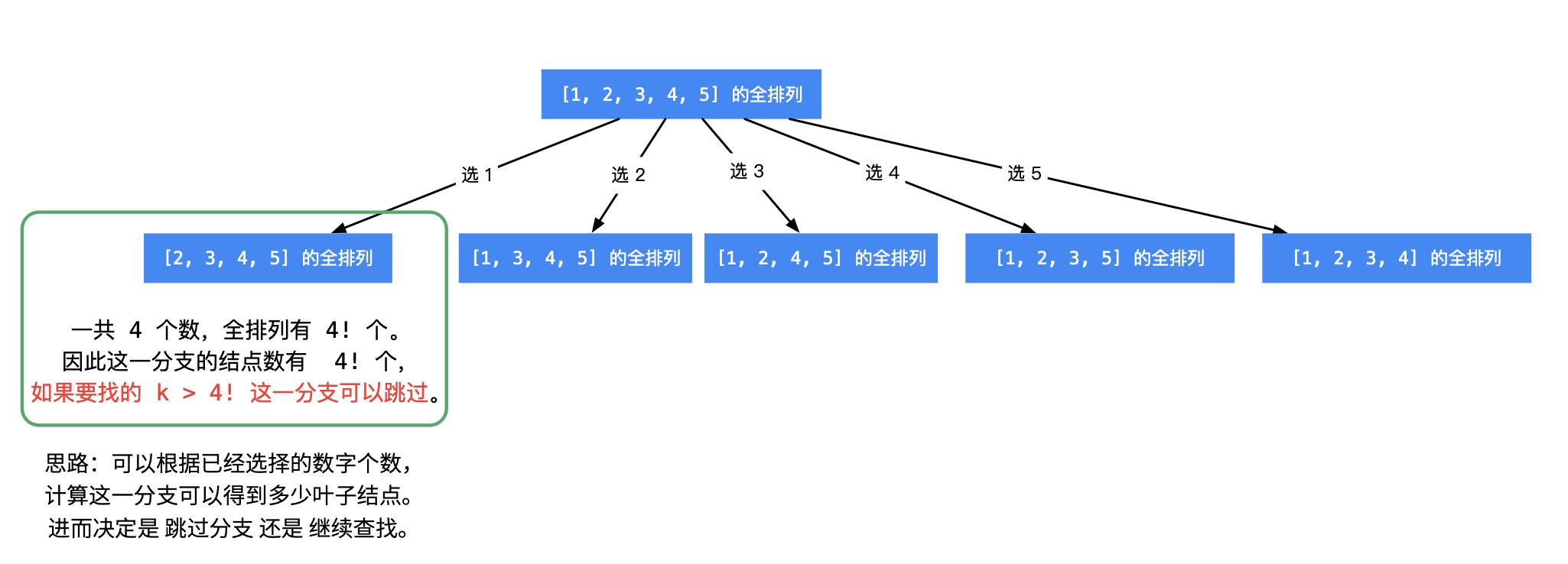
所求排列 一定在叶子结点处得到，进入每一个分支，可以根据已经选定的数的个数，进而计算还未选定的数的个数，然后计算阶乘，就知道这一个分支的 叶子结点 的个数：
如果 k 大于这一个分支将要产生的叶子结点数，直接跳过这个分支，这个操作叫「剪枝」；
如果 k 小于等于这一个分支将要产生的叶子结点数，那说明所求的全排列一定在这一个分支将要产生的叶子结点里，需要递归求解。

编码注意事项：

计算阶乘的时候，可以使用循环计算。注意：0!=1，它表示了没有数可选的时候，即表示到达叶子结点了，排列数只剩下 1 个；
题目中说「给定 n 的范围是 [1, 9]」，可以把从 0 到 9 的阶乘计算好，放在一个数组里，可以根据索引直接获得阶乘值；
编码的时候，+1 还是 −1 ，大于还是大于等于，这些不能靠猜。常见的做法是：代入一个具体的数值，认真调试。

三、代码

import java.util.Arrays;

public class Solution {
    private boolean[] used;
    private int[] factorial;
    private int n;
    private int k;
    /**
     * 计算阶乘数组
     *
     * @param n
     */
    private void calculateFactorial(int n) {
        factorial = new int[n + 1];
        factorial[0] = 1;
        for (int i = 1; i <= n; i++) {
            factorial[i] = factorial[i - 1] * i;
        }
    }
    public  String getPermutation(int n, int k) {
        this.n=n;
        this.k=k;
        calculateFactorial(n);
        // 查找全排列需要的布尔数组
        used = new boolean[n + 1];
        Arrays.fill(used, false);

        StringBuilder path = new StringBuilder();
        dfs(0, path);
        return path.toString();
    }
    /**
     * @param index 在这一步之前已经选择了几个数字，其值恰好等于这一步需要确定的下标位置
     * @param path
     */
    private void dfs(int index,StringBuilder path) {
        if (index == n) {
            return;
        }
        // 计算还未确定的数字的全排列的个数，第 1 次进入的时候是 n - 1
        int cnt = factorial[n - 1 - index];

        //本层集合中元素
        for (int i = 1; i <=n; i++) {
            if(used[i]){
                continue;
            }
            if(cnt<k){
                k-=cnt;
                continue;
            }
            path.append(i);
            used[i]=true;
            dfs(index+1, path);
            // 注意 1：不可以回溯（重置变量），算法设计是「一下子来到叶子结点」，没有回头的过程
            // 注意 2：这里要加 return，后面的数没有必要遍历去尝试了
            return;
        }
    }

    public static void main(String[] args) {
        Solution2 solution2=new Solution2();
        System.out.println(solution2.getPermutation(3,3));
    }
}

四、复杂度分析

时间复杂度：O(N^2)。最坏是要找到第N!个，但是第1层你只需要比较N-1次，第2层比较N-2次，以此类推。
空间复杂度：O(N)，nums、used、path 都与 N 等长，factorial 数组就 10 个数，是常数级别的。

欢迎关注微信公众号【算法攻城师】