Codeforces Round #705 (Div. 2) D. GCD of an Array

Posted 2021-08-11 TURNINING

传送门
题意：给你一个数组含有n个数，同时进行q次操作，每次操作让x位置上的数乘上v，每次操作后输出给个数组的gcd。

最大公约数：

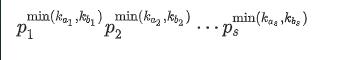
于是我们有这样的想法，对于每个素数，我们维护n个数中的最小值。显然区间最小值可以用线段树维护，但那样我们不是要开s课线段树？内存显然不够用。

1.考虑离线处理 每次算乘上这个数后对结果的贡献(指数是相加的)，同样对于刚开始的n个数，我们可以看作最开始每个数都是1，然后依次乘上ai。

每次算贡献 我们可以一次把所有p的贡献算完，算完后再清空线段树就可以重复利用了。

#include<bits/stdc++.h>
using namespace std;

#define lsn (u << 1)
#define rsn (u << 1 | 1)
#define mid (l + r >> 1)

typedef long long ll;
typedef unsigned long long ull;

typedef pair<int, int> P;
typedef pair<double, double> PD;

const int MAXN = 2e5 + 10;
const int MAX_LEN = 100000 + 10;
const int MAX_LOG_V = 22;
const int INF = 0x3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-7;
const ull B = 100000007;

int n, q;

struct Node {
    int id, t, v;
};

vector<Node> a[MAXN];
int tr[4*MAXN];
ll ans[2*MAXN];

ll qpow(ll x, int y) {
    ll res = 1;
    while(y) {
        if(y & 1) res = res * x % mod;
        y >>= 1;
        x = x * x % mod;
    }
    return res;
} 

void pushup(int u) {
    tr[u] = min(tr[lsn], tr[rsn]);
}

void add(int u, int l, int r, int p, int v) {
    if(l == r && l == p) tr[u] += v;
    else {
        if(p <= mid) add(lsn, l, mid, p, v);
        else add(rsn, mid+1, r, p, v);
        pushup(u);
    }
}

void solve() {
    scanf("%d %d", &n, &q);
    for(int i = 1; i <= n + q; i++) ans[i] = 1;
    for(int i = 1; i <= n; i++) {
        int x; scanf("%d", &x);
        for(int j = 2; j * j <= x; j++) {
            if(x % j != 0) continue;
            int cnt = 0;
            while(x % j == 0) {
                cnt++;
                x /= j;
            }
            a[j].emplace_back(Node{i, i, cnt});
        }   
        if(x != 1) a[x].emplace_back(Node{i, i, 1});
    } 
    for(int i = n+1; i <= n+q; i++) {
        int id, x; scanf("%d %d", &id, &x);
        for(int j = 2; j * j <= x; j++) {
            if(x % j != 0) continue;
            int cnt = 0;
            while(x % j == 0) {
                cnt++;
                x /= j;
            }
            a[j].emplace_back(Node{id, i, cnt});
        }   
        if(x != 1) a[x].emplace_back(Node{id, i, 1});
    }
    for(int i = 2; i < MAXN; i++) {
        int last = 0;
        for(auto p : a[i]) {
            add(1, 1, n, p.id, p.v);
            if(tr[1] == last) continue;
            ans[p.t] = ans[p.t] * qpow(i, tr[1]-last) % mod;    //在p.t时刻素数i对结果的贡献。
            last = tr[1]; 
        }
        for(auto p : a[i]) {
            add(1, 1, n, p.id, -p.v);
        }
    }
    for(int i = 2; i <= n + q; i++) {
        ans[i] = ans[i] * ans[i-1] % mod;
    }
    for(int i = n+1; i <= n+q; i++) {
        printf("%lld\\n", ans[i]);
    }
}


int main() {
    //ios::sync_with_stdio(false);
    int t = 1; //scanf("%d", &t);
    while (t--) {
        solve();
    }
    return 0;
}

2.动态开点线段树。
就非要开2e5个线段树

引用真是个好东西

#include<bits/stdc++.h>
using namespace std;

#define lsn (u << 1)
#define rsn (u << 1 | 1)
#define mid (l + r >> 1)

typedef long long ll;
typedef unsigned long long ull;

typedef pair<int, int> P;
typedef pair<double, double> PD;

const int MAXN = 2e5 + 10;
const int MAX_LEN = 100000 + 10;
const int MAX_LOG_V = 22;
const int INF = 0x3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-7;
const ull B = 100000007;

int n, q;

ll qpow(ll x, ll y) {
    ll res = 1;
    while(y) {
        if(y & 1) res = res * x % mod;
        y >>= 1;
        x = x * x % mod; 
    }
    return res;
} 

const int maxm = 1e7 + 5;
int ls[maxm], rs[maxm], tr[maxm], rt[maxm], tot;

void pushup(int u) {
    tr[u] = min(tr[ls[u]], tr[rs[u]]);   
}

void add(int &u, int l, int r, int p, int v) {
    if(!u) u = ++tot;
    if(l == r) { tr[u] += v; return ; }
    else {
        if(p <= mid) add(ls[u], l, mid, p, v);
        else add(rs[u], mid+1, r, p, v);
        pushup(u);
    }
}

void solve() {
    scanf("%d %d", &n, &q);
    ll ans = 1;
    for(int i = 1; i <= n; i++){
        int x; scanf("%d", &x);
        for(int j = 2; j * j <= x; j++) {
            if(x % j != 0) continue;
            int cnt = 0;
            while(x % j == 0) {
                cnt++;
                x /= j;
            }
            int pre = tr[rt[j]];
            add(rt[j], 1, n, i, cnt);
            ans = ans * qpow(j, tr[rt[j]]-pre) % mod;
        }
        if(x != 1) {
            int pre = tr[rt[x]];
            add(rt[x], 1, n, i, 1);
            ans = ans * qpow(x, tr[rt[x]]-pre) % mod;
        }
    }
    for(int i = 1; i <= q; i++) {
        int p, x; scanf("%d %d", &p, &x);
        for(int j = 2; j * j <= x; j++) {
            if(x % j != 0) continue;
            int cnt = 0;
            while(x % j == 0) {
                cnt++;
                x /= j;
            }
            int pre = tr[rt[j]];
            add(rt[j], 1, n, p, cnt);
            ans = ans * qpow(j, tr[rt[j]]-pre) % mod;
        }
        if(x != 1) {
            int pre = tr[rt[x]];
            add(rt[x], 1, n, p, 1);
            ans = ans * qpow(x, tr[rt[x]]-pre) % mod;
        }
        printf("%lld\\n", ans);
    }
}


int main() {
    //ios::sync_with_stdio(false);
    int t = 1; //scanf("%d", &t);
    while (t--) {
        solve();
    }
    return 0;
}