剑指Offer 04. 二维数组中的查找

Posted 2021-08-08 寻7

LeetCode_剑指Offer

• • • • 04. 二维数组中的查找
      • • 一、题目描述
        • 二、示例描述
        • 三、解法分析

04. 二维数组中的查找

一、题目描述

• 在一个 n * m 的二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个高效的函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

二、示例描述

• 示例:
  
  现有矩阵 matrix 如下：
  [
    [1,   4,  7, 11, 15],
    [2,   5,  8, 12, 19],
    [3,   6,  9, 16, 22],
    [10, 13, 14, 17, 24],
    [18, 21, 23, 26, 30]
  ]
  给定 target = 5，返回 true。
  给定 target = 20，返回 false。
  
  限制：
  0 <= n <= 1000
  0 <= m <= 1000
  

三、解法分析

方案一：暴力求解

• 遍历二维数组，将数组中的每个元素与其他元素进行对比，判断目标值是否在二维数组中存在。如果找到一个元素等于目标值，则返回 true。如果遍历完毕仍未找到等于目标值的元素，则返回 false。

代码实现：

class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {//二维数组为空
            return false;
        }
        int rows = matrix.length, columns = matrix[0].length;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                if (matrix[i][j] == target) {
                    return true;
                }
            }
        }
        return false;
    }
}

算法复杂度分析：

• 时间复杂度：O(nm)，二维数组中的每个元素都被遍历，因此时间复杂度为二维数组的大小。
• 空间复杂度：O(1)

方案二：线性查找

• 由于给定的二维数组具备每行从左到右递增以及每列从上到下递增的特点，当访问到一个元素时，可以排除数组中的部分元素。

• 从二维数组的左上角或者右下角开始查找，没法排除数组元素。例如左上角开始，如果当前元素小于目标值，则目标值可能在下面也可能在右边，无法排除元素。

• @_@ 从二维数组的左下或右上角开始查找，则可以在每次查询后排除部分元素。比如从右上角开始查找，如果当前元素等于目标值，则返回 true。如果当前元素大于目标值，则移到左边一列。如果当前元素小于目标值，则移到下边一行。

• 可以证明这种方法不会错过目标值。如果当前元素大于目标值，说明当前元素的下边的所有元素都一定大于目标值，因此往下查找不可能找到目标值，往左查找可能找到目标值。如果当前元素小于目标值，说明当前元素的左边的所有元素都一定小于目标值，因此往左查找不可能找到目标值，往下查找可能找到目标值。

• 若数组为空，返回 false
  
  初始化行下标为 0，列下标为二维数组的列数减 1
  
  重复下列步骤，直到行下标或列下标超出边界
  	获得当前下标位置的元素 num
  	如果 num 和 target 相等，返回 true
  	如果 num 大于 target，列下标减 1
  	如果 num 小于 target，行下标加 1
  	
  循环体执行完毕仍未找到元素等于 target ，说明不存在这样的元素，返回 false`
  

举例：查找元素14

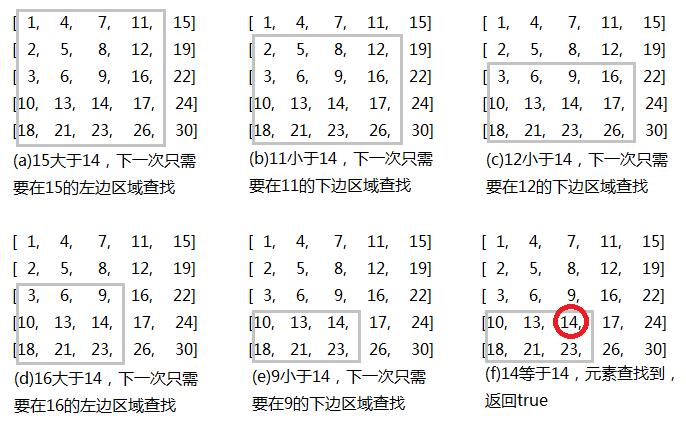
代码实现：

class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return false;
        }
        int rows = matrix.length, columns = matrix[0].length;
        int row = 0, column = columns - 1;
        while (row < rows && column >= 0) {
            int num = matrix[row][column];
            if (num == target) {
                return true;
            } else if (num > target) {
                column--;
            } else {
                row++;
            }
        }
        return false;
    }
}

算法复杂度分析：

• 时间复杂度：O(n+m)，二维数组从右上角到左下角
• 空间复杂度：O(1)