树状数组
Posted EVANGELION-01
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了树状数组相关的知识,希望对你有一定的参考价值。
时间复杂度:o(logn)
支持:
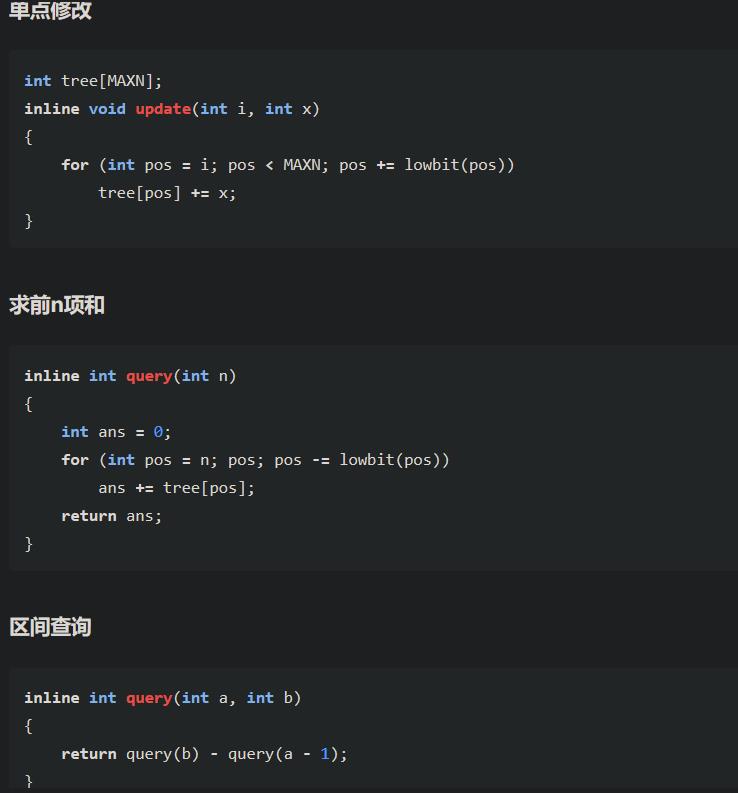
1.单点修改
2.区间查询:查询一个区间内所有元素的和
对 进行区间查询只需查询
和
然后相减即可(前缀和就是这样进行区间查询的),所以我们可以把区间查询问题转化为求前n项和的问题。
可以用一个数组 ![[公式]](https://www.zhihu.com/equation?tex=C) 维护若干个小区间,单点修改时,只更新包含这一元素的区间;求前n项和时,通过将区间进行组合,得到从1到n的区间,然后对所有用到的区间求和。实际上,设原数组是
维护若干个小区间,单点修改时,只更新包含这一元素的区间;求前n项和时,通过将区间进行组合,得到从1到n的区间,然后对所有用到的区间求和。实际上,设原数组是 ![[公式]](https://www.zhihu.com/equation?tex=A) ,如果
,如果 ![[公式]](https://www.zhihu.com/equation?tex=C_i) 维护的区间是
维护的区间是 ![[公式]](https://www.zhihu.com/equation?tex=%5BA_i%2C+A_i%5D) ,此结构就相当于普通数组(还浪费了一倍内存);如果
,此结构就相当于普通数组(还浪费了一倍内存);如果 ![[公式]](https://www.zhihu.com/equation?tex=C_i) 维护的区间就是
维护的区间就是 ![[公式]](https://www.zhihu.com/equation?tex=%5B1%2CA_i%5D) ,此结构就相当于前缀和。
,此结构就相当于前缀和。

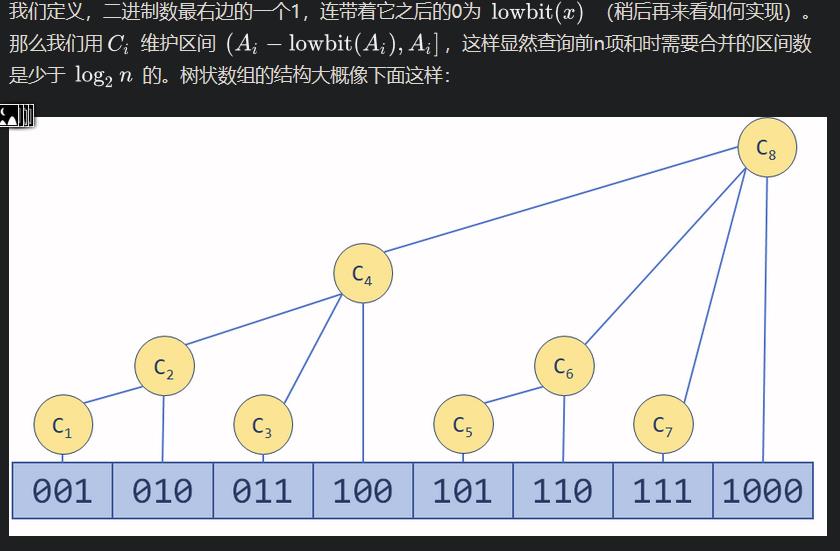
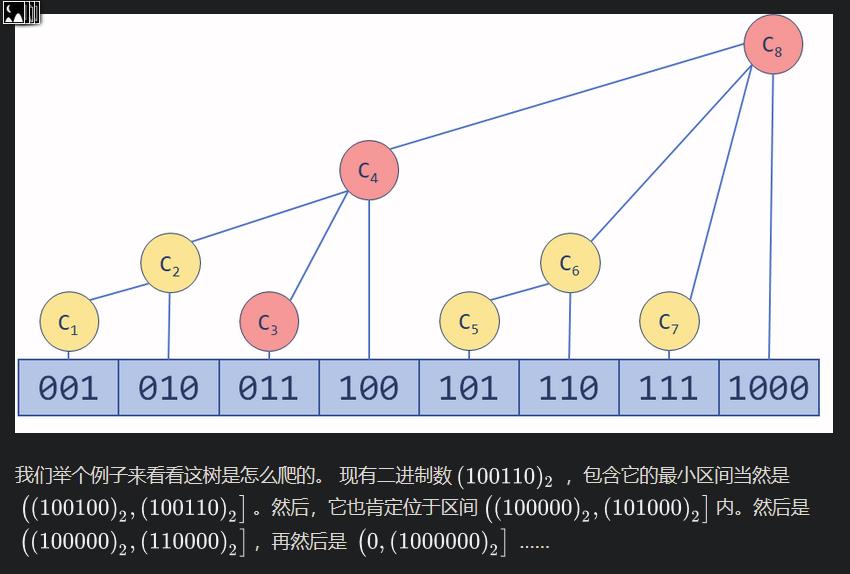
注意区间左开右闭
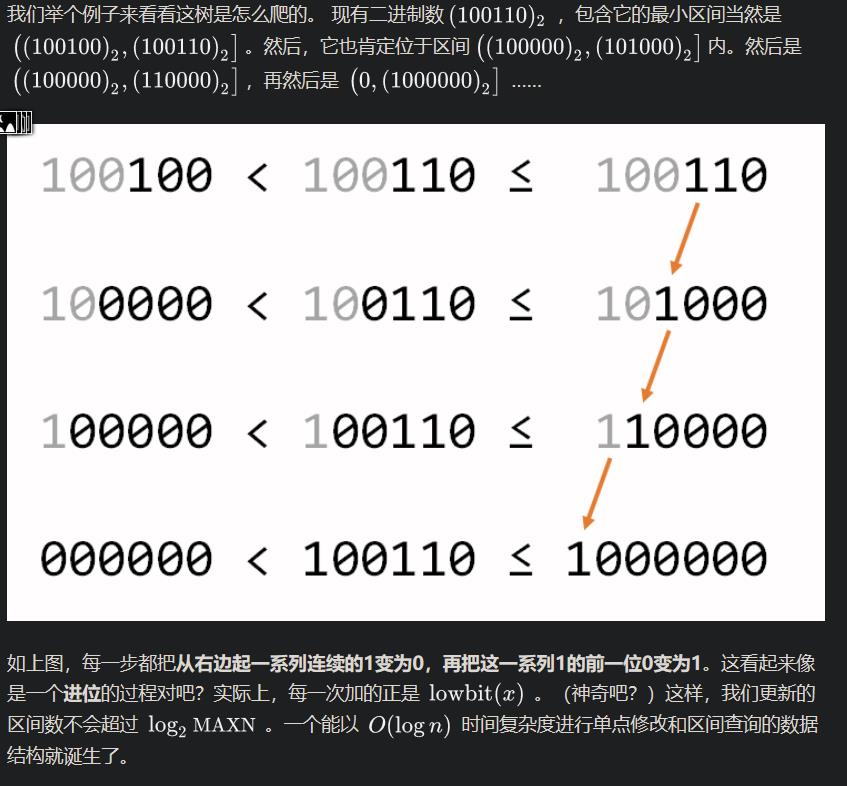
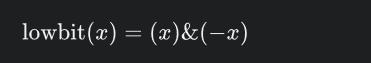

以上是关于树状数组的主要内容,如果未能解决你的问题,请参考以下文章