实验二 K-近邻算法及应用
Posted 小虾米
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了实验二 K-近邻算法及应用相关的知识,希望对你有一定的参考价值。
K-近邻算法及应用
| 所在班级 | 机器学习 |
| 实验要求 | 作业要求 |
| 学习目标 | 理解K-近邻算法原理,能实现算法K近邻算法; |
| 学号 | 3180701310 |
【实验目的】
理解K-近邻算法原理,能实现算法K近邻算法;
掌握常见的距离度量方法;
掌握K近邻树实现算法;
针对特定应用场景及数据,能应用K近邻解决实际问题。
【实验内容】
实现曼哈顿距离、欧氏距离、闵式距离算法,并测试算法正确性。
实现K近邻树算法;
针对iris数据集,应用sklearn的K近邻算法进行类别预测。
针对iris数据集,编制程序使用K近邻树进行类别预测。
【实验报告要求】
对照实验内容,撰写实验过程、算法及测试结果;
代码规范化:命名规则、注释;
分析核心算法的复杂度;
查阅文献,讨论K近邻的优缺点;
举例说明K近邻的应用场景。
【实验运行结果】
【实验代码及其注释】
一、距离度量
利用python代码遍历三个点中,与1点距离最近的点
# 导入所需要的包
import math
from itertools import combinations
# 当p=1时,就是曼哈顿距离;
# 当p=2时,就是欧氏距离;
# 当p=inf时,就是闵式距离。
# 函数主要用于距离测算
def L(x, y, p=2):
# x1 = [1, 1], x2 = [5,1]
if len(x) == len(y) and len(x) > 1:
sum = 0
for i in range(len(x)):
sum += math.pow(abs(x[i] - y[i]), p)
return math.pow(sum, 1/p)
else:
return 0
# 输入样例,该列来源于课本
x1 = [1, 1]
x2 = [5, 1]
x3 = [4, 4]
# 计算x1与x2和x3之间的距离
for i in range(1, 5): # i从1到4
r = { \'1-{}\'.format(c):L(x1, c, p=i) for c in [x2, x3]} # 创建一个字典
print(min(zip(r.values(), r.keys()))) # 当p=i时选出x2和我x3中距离x1最近的点
输出:

二、编写K-近邻算法
python实现,遍历所有数据点,找出n个距离最近的点的分类情况,少数服从多数(不使用直接的python中现有的K-近邻算法包)
# 导包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from collections import Counter
# data 输入数据
iris = load_iris() # 获取python中鸢尾花Iris数据集
df = pd.DataFrame(iris.data, columns=iris.feature_names) # 将数据集使用DataFrame建表
df[\'label\'] = iris.target # 将表的最后一列作为目标列
df.columns = [\'sepal length\', \'sepal width\', \'petal length\', \'petal width\', \'label\'] # 定义表中每一列
# data = np.array(df.iloc[:100, [0, 1, -1]])
df # 将建好的表显示在屏幕上查看
输出:


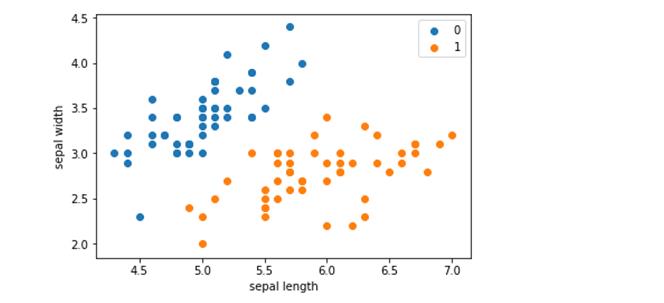
# 绘制数据散点图
plt.scatter(df[:50][\'sepal length\'], df[:50][\'sepal width\'], label=\'0\') # 绘制前50个数据的散点图
plt.scatter(df[50:100][\'sepal length\'], df[50:100][\'sepal width\'], label=\'1\') # 绘制50-100个数据的散点图
plt.xlabel(\'sepal length\')
plt.ylabel(\'sepal width\') # 设置x,y轴坐标名
plt.legend() # 绘图
注释:
train_test_split()是分离器函数,用于将数组或矩阵划分为训练集和测试集,
函数样式为:X_train, X_test, y_train, y_test = train_test_split(train_data, train_target, test_size, random_state,shuffle)
train_data:待划分的样本数据
train_target:待划分的对应样本数据的样本标签
test_size:
1)浮点数,在0 ~ 1之间,表示样本占比(test_size = 0.3,则样本数据中有30%的数据作为测试数据,记入X_test,其余70%数据记入X_train,
同时适用于样本标签);
2)整数,表示样本数据中有多少数据记入X_test中,其余数据记入X_train)
data = np.array(df.iloc[:100, [0, 1, -1]]) # iloc函数:通过行号来取行数据,读取数据前100行的第0,1列和最后一列
# X为data数据集中去除最后一列所形成的新数据集
# y为data数据集中最后一列数据所形成的新数据集
X, y = data[:,:-1], data[:,-1]
# 选取训练集,和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# 建立一个类KNN,用于k-近邻的计算
class KNN:
#初始化
def __init__(self, X_train, y_train, n_neighbors=3, p=2): # 初始化数据,neighbor表示邻近点,p为欧氏距离
self.n = n_neighbors
self.p = p
self.X_train = X_train
self.y_train = y_train
def predict(self, X):
# X为测试集
knn_list = []
for i in range(self.n): # 遍历邻近点
dist = np.linalg.norm(X - self.X_train[i], ord=self.p) # 计算训练集和测试集之间的距离
knn_list.append((dist, self.y_train[i])) # 在列表末尾添加一个元素
for i in range(self.n, len(self.X_train)): # 3-20
max_index = knn_list.index(max(knn_list, key=lambda x: x[0])) # 找出列表中距离最大的点
dist = np.linalg.norm(X - self.X_train[i], ord=self.p) # 计算训练集和测试集之间的距离
if knn_list[max_index][0] > dist: # 若当前数据的距离大于之前得出的距离,就将数值替换
knn_list[max_index] = (dist, self.y_train[i])
# 统计
knn = [k[-1] for k in knn_list]
count_pairs = Counter(knn) # 统计标签的个数
max_count = sorted(count_pairs, key=lambda x:x)[-1] # 将标签升序排列
return max_count
# 计算测试算法的正确率
def score(self, X_test, y_test):
right_count = 0
n = 10
for X, y in zip(X_test, y_test):
label = self.predict(X)
if label == y:
right_count += 1
return right_count / len(X_test)
11、
clf = KNN(X_train, y_train) # 调用KNN算法进行计算
12、
clf.score(X_test, y_test) # 计算正确率
输出:

test_point = [6.0, 3.0] # 用于算法测试的数据
print(\'Test Point: {}\'.format(clf.predict(test_point))) # 结果
输出:

plt.scatter(df[:50][\'sepal length\'], df[:50][\'sepal width\'], label=\'0\') # 将数据的前50个数据绘制散点图
plt.scatter(df[50:100][\'sepal length\'], df[50:100][\'sepal width\'], label=\'1\') # 将数据的50-100个数据绘制散点图
plt.plot(test_point[0], test_point[1], \'bo\', label=\'test_point\') # 将测试数据点绘制在图中
plt.xlabel(\'sepal length\')
plt.ylabel(\'sepal width\') # x,y轴命名
plt.legend() # 绘图
输出:

三、使用scikitlearn中编好的包直接调用实现K-近邻算法
sklearn.neighbors.KNeighborsClassifier
n_neighbors: 临近点个数
p: 距离度量
algorithm: 近邻算法,可选{\'auto\', \'ball_tree\', \'kd_tree\', \'brute\'}
weights: 确定近邻的权重
15、
# 导包
from sklearn.neighbors import KNeighborsClassifier
# 调用
clf_sk = KNeighborsClassifier()
clf_sk.fit(X_train, y_train)
输出:

clf_sk.score(X_test, y_test) # 计算正确率
输出:

四、针对iris数据集,编制程序使用K近邻树进行类别预测
建造kd树
# 建造kd树
# kd-tree 每个结点中主要包含的数据如下:
class KdNode(object):
def __init__(self, dom_elt, split, left, right):
self.dom_elt = dom_elt#结点的父结点
self.split = split#划分结点
self.left = left#做结点
self.right = right#右结点
class KdTree(object):
def __init__(self, data):
k = len(data[0])#数据维度
#print("创建结点")
#print("开始执行创建结点函数!!!")
def CreateNode(split, data_set):
#print(split,data_set)
if not data_set:#数据集为空
return None
#print("进入函数!!!")
data_set.sort(key=lambda x:x[split])#开始找切分平面的维度
#print("data_set:",data_set)
split_pos = len(data_set)//2 #取得中位数点的坐标位置(求整)
median = data_set[split_pos]
split_next = (split+1) % k #(取余数)取得下一个节点的分离维数
return KdNode(
median,
split,
CreateNode(split_next, data_set[:split_pos]),#创建左结点
CreateNode(split_next, data_set[split_pos+1:]))#创建右结点
#print("结束创建结点函数!!!")
self.root = CreateNode(0, data)#创建根结点
#KDTree的前序遍历
def preorder(root):
print(root.dom_elt)
if root.left:
preorder(root.left)
if root.right:
preorder(root.right)
遍历kd树
# 遍历kd树
#KDTree的前序遍历
def preorder(root):
print(root.dom_elt)
if root.left:
preorder(root.left)
if root.right:
preorder(root.right)
from math import sqrt
from collections import namedtuple
# 定义一个namedtuple,分别存放最近坐标点、最近距离和访问过的节点数
result = namedtuple("Result_tuple",
"nearest_point nearest_dist nodes_visited")
#搜索开始
def find_nearest(tree, point):
k = len(point)#数据维度
def travel(kd_node, target, max_dist):
if kd_node is None:
return result([0]*k, float("inf"), 0)#表示数据的无
nodes_visited = 1
s = kd_node.split #数据维度分隔
pivot = kd_node.dom_elt #切分根节点
if target[s] <= pivot[s]:
nearer_node = kd_node.left #下一个左结点为树根结点
further_node = kd_node.right #记录右节点
else: #右面更近
nearer_node = kd_node.right
further_node = kd_node.left
temp1 = travel(nearer_node, target, max_dist)
nearest = temp1.nearest_point# 得到叶子结点,此时为nearest
dist = temp1.nearest_dist #update distance
nodes_visited += temp1.nodes_visited
print("nodes_visited:", nodes_visited)
if dist < max_dist:
max_dist = dist
temp_dist = abs(pivot[s]-target[s])#计算球体与分隔超平面的距离
if max_dist < temp_dist:
return result(nearest, dist, nodes_visited)
# -------
#计算分隔点的欧式距离
temp_dist = sqrt(sum((p1-p2)**2 for p1, p2 in zip(pivot, target)))#计算目标点到邻近节点的Distance
if temp_dist < dist:
nearest = pivot #更新最近点
dist = temp_dist #更新最近距离
max_dist = dist #更新超球体的半径
print("输出数据:" , nearest, dist, max_dist)
# 检查另一个子结点对应的区域是否有更近的点
temp2 = travel(further_node, target, max_dist)
nodes_visited += temp2.nodes_visited
if temp2.nearest_dist < dist: # 如果另一个子结点内存在更近距离
nearest = temp2.nearest_point # 更新最近点
dist = temp2.nearest_dist # 更新最近距离
return result(nearest, dist, nodes_visited)
return travel(tree.root, point, float("inf")) # 从根节点开始递归
# 数据测试
data= [[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]
kd=KdTree(data)
preorder(kd.root)
输出:

# 导包
from time import clock
from random import random
# 产生一个k维随机向量,每维分量值在0~1之间
def random_point(k):
return [random() for _ in range(k)]
# 产生n个k维随机向量
def random_points(k, n):
return [random_point(k) for _ in range(n)]
# 输入数据进行测试
ret = find_nearest(kd, [3,4.5])
print (ret)
输出:

N = 400000
t0 = clock()
kd2 = KdTree(random_points(3, N)) # 构建包含四十万个3维空间样本点的kd树
ret2 = find_nearest(kd2, [0.1,0.5,0.8]) # 四十万个样本点中寻找离目标最近的点
t1 = clock()
print ("time: ",t1-t0, "s")
print (ret2)
输出:

查阅文献,讨论K近邻的优缺点;
1.k kk近邻法是基本且简单的分类与回归方法。k kk近邻法的基本做法是:对给定的训练实例点和输入实例点,首先确定输入实例点的k kk个最近邻训练实例点,然后利用这k kk个训练实例点的类的多数来预测输入实例点的类。
2.k kk近邻模型对应于基于训练数据集对特征空间的一个划分。k kk近邻法中,当训练集、距离度量、k kk值及分类决策规则确定后,其结果唯一确定。
3.k kk近邻法三要素:距离度量、k kk值的选择和分类决策规则。常用的距离度量是欧氏距离及更一般的pL距离。k kk值小时,k kk近邻模型更复杂;k kk值大时,k kk近邻模型更简单。k kk值的选择反映了对近似误差与估计误差之间的权衡,通常由交叉验证选择最优的k kk。
常用的分类决策规则是多数表决,对应于经验风险最小化。
4.k kk近邻法的实现需要考虑如何快速搜索k个最近邻点。kd树是一种便于对k维空间中的数据进行快速检索的数据结构。kd树是二叉树,表示对k kk维空间的一个划分,其每个结点对应于k kk维空间划分中的一个超矩形区域。利用kd树可以省去对大部分数据点的搜索, 从而减少搜索的计算量。
举例说明K近邻的应用场景。
稀有类检测的目标是为无类别标签的数据集中的每个类,特别是仅含少量数据样本的稀有类,寻找到至少一个数据样本以证明数据集中存在这些类.该技术在金融欺诈检测及网络入侵检测等现实问题中具有广泛的应用场景.但是,现有的稀有类检测算法往往存在以下问题:(1)时间复杂度比较高;或(2)对原始数据集需要一定的先验知识,如数据集中各类数据样本所占比例等.提出了一种基于k邻近图的无先验快速稀有类检测算法KRED,通过利用稀有类数据样本在小范围内紧密分布所造成的与周边数据分布的不一致性来定位稀有类.为此,KRED将给定数据集转化为k邻近图,并计算图中各顶点入度和边长的变化.最后,将以上变化最大的顶点对应的数据样本作为稀有类的候选样本.实验结果表明:KRED有效提高了发现数据集中各个类的效率,明显缩短了算法运行所需时间.
随着基于位置服务的广泛应用,时间依赖路网上的对象查询逐渐成为研究热点.以往研究大多只针对时间依赖路网上的静态对象(如加油站,餐厅等),未考虑到移动对象(如出租车)的情况,而移动对象的查询在日常生活中有着非常广泛的应用场景.因此,文中提出了一种针对时间依赖路网上的移动对象K近邻查询算法TD-MOKNN,该算法分为预处理阶段和查询阶段.在预处理阶段,通过建立路网和网格索引,提出了一种新的移动对象到路网的映射方法,解除了以往研究假设移动对象恰好在路网顶点上的限制;在查询阶段,采用启发式搜索,借助倒排网格索引计算了一种新的高效启发值,通过预处理信息和启发值设计了高效K近邻查询算法,并给出了算法的正确性证明和时间复杂度分析.实验验证了所提算法的有效性,相比现有算法,TD-MOKNN算法在遍历顶点数和响应时间上分别减少了55.91%和54.57%,查询效率平均提升了55.2%.
【实验小结】
(1)K-近邻算法不仅可以用于分类,还可以用于回归。通过找出一个样本的k个最近邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。
(2)比起其他机器学习方法,k-近邻算法是最简单最有效的分类数据算法,使用算法时必须有接近实际数据的训练样本数据。但是该算法的缺点也很多,最大的一点是无法给出数据的内在含义。事实上k决策树是k-近邻算法的优化版本,比起前者,决策树有效减少了储存空间和计算空间的开销。
以上是关于实验二 K-近邻算法及应用的主要内容,如果未能解决你的问题,请参考以下文章