算法和数据结构解析-6 : 链表问题

Posted 2022-07-18 鮀城小帅

链表（Linked List）是一种常见的基础数据结构，是一种线性表，但是并不会按线性的顺序存储数据，而是在每一个节点里存到下一个节点的指针（Pointer）。

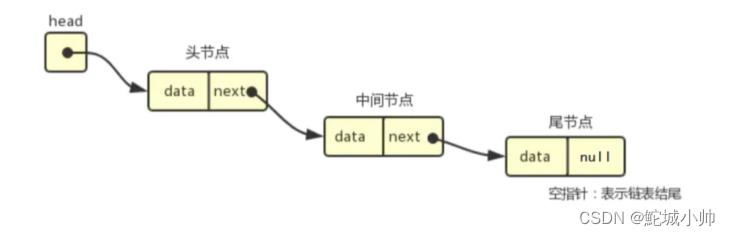
由于不必须按顺序存储，链表在插入的时候可以达到 O(1)的复杂度，比另一种线性表 —— 顺序表快得多，但是查找一个节点或者访问特定编号的节点则需要 O(n) 的时间，而顺序表相应的时间复杂度分别是 O(n) 和 O(1)。

链表允许插入和移除表上任意位置上的节点，但是不允许随机存取。链表有很多种不同的类型：单向链表，双向链表以及循环链表。

1. 反转链表

1.1 题目说明

反转一个单链表。

示例:

输入: 1->2->3->4->5->NULL

输出: 5->4->3->2->1->NULL

进阶:

你可以迭代或递归地反转链表。你能否用两种方法解决这道题？

1.2 分析

链表的节点结构ListNode已经定义好，我们发现，反转链表的过程，其实跟val没有关系，只要把每个节点的next指向之前的节点就可以了。

从代码实现上看，可以有迭代和递归两种形式。

 1.3 方法一：迭代

    /**
     * 方法一：迭代
     * @param head
     * @return
     */
    public ListNode reverseList(ListNode head)
        // 定义两个指针，指向当前访问的节点,以及上一个节点
        ListNode curr = head;
        ListNode prev = null;

        // 依此迭代链表中的节点，将next指针指向prev
        while(curr != null)
            // 假如有 1->2->3
            // 临时保存当前节点的下一个节点，curr=1,那么curr.next=2
            ListNode tempNode = curr.next;
            // 反转，将curr=1->2(next)反转为curr=1->null(prev)
            curr.next = prev;
            // 更新指针，当前指针变为之前的next,上一个指针变为curr。此时head=1->null已经反转好，将prev=curr=1,作为下一个基点反转的next
            prev = curr;
            // 此时，将curr=1.next=2，进入下一轮继续反转。
            curr = tempNode;
        
        return prev;
    

复杂度分析

时间复杂度：O(n)，假设 n 是链表的长度，时间复杂度是 O(n)。

空间复杂度：O(1)

1.4 方法二：递归

    /**
     * 方法二：递归
     * @param head
     * @return
     */
    public ListNode reverseList2(ListNode head)

        // 当head.next==null，说明是最后一个节点，比如5->null
        if(head == null || head.next == null)
            return head;
        
        
        // 获取当前节点的下一个节点，比如当前是1，next就是2
        ListNode listRest = head.next;
        // 递归调用，因为2->3，所以继续调用
        ListNode listNodeRest = reverseList2(listRest);
        
        // 递归调用return，此时将 node(m+1) -> node(m)，也就是反转。即 4->5反转为 5->4 
        listRest.next = head;
        // 头结点指向null 4->null，因为会不断跳出，在return后，继续反转，所以4->3。直到2->1，此时1->null。然后结束
        head.next = null;
        
        return listNodeRest;
    

 2.合并两个有序链表

2.1 题目说明

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 

示例：

输入：1->2->4, 1->3->4

输出：1->1->2->3->4->4

2.2 分析

链表节点结构已经定义好，而且已经做了升序排列。现在我们需要分别遍历两个链表，然后依次比较，按从小到大的顺序生成新的链表就可以了。这其实就是“归并排序”的思路。

2.3 方法一：迭代

最简单的想法，就是逐个遍历两个链表中的节点，依次比对。

我们假设原链表为list1和list2。只要它们都不为空，就取出当前它们各自的头节点就行比较。值较小的那个结点选取出来，加入到结果链表中，并将对应原链表的头（head）指向下一个结点；而值较大的那个结点则保留，接下来继续做比对。

另外，为了让代码更加简洁，我们可以引入一个哨兵节点（sentinel），它的next指向结果链表的头结点，它的值设定为-1。

    /**
     * 方法一：迭代
     * @param l1
     * @param l2
     * @return
     */
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) 

        // 定义一个哨兵节点
        ListNode sentinel = new ListNode(-1);
        // 保存当前结果链表里的最后一个节点，作为判断比较的“前一个节点”
        ListNode prev = sentinel;

        // 迭代遍历两个链表，直到至少有一个为Null
        while (l1 != null && l2 != null)
            // 比较当前两个链表的头节点，较小的那个按在结果链表末尾
            if (l1.value < l2.value)
                prev.next = l1;     // 将l1头节点连接到prev后面
                prev = l1;          // 指针向前移动，以下一个节点作为链表头节点
                l1 = l1.next;
            else
                prev.next = l2;     // 将l2头节点连接到prev后面
                prev = l2;          // 指针向前移动，以下一个节点作为链表头节点
                l2 = l2.next;
            
        
        // 循环结束，最多还有一个链表没有遍历完成，因为已经排序，可以直接把剩余节点接到结果链表上
        prev.next = (l1 == null)? l2:l1;
        return sentinel.next;
    

复杂度分析

时间复杂度：O(n + m) ，其中 n 和 m 分别为两个链表的长度。因为每次循环迭代中，l1 和 l2 只有一个元素会被放进合并链表中， 因此 while 循环的次数不会超过两个链表的长度之和。所有其他操作的时间复杂度都是常数级别的，因此总的时间复杂度为 O(n+m)。

空间复杂度：O(1)。我们只需要常数的空间存放若干变量。

2.4 方法二：递归

用递归的方式同样可以实现上面的过程。

当两个链表都不为空时，我们需要比对当前两条链的头节点。取出较小的那个节点；而两条链其余的部分，可以递归调用，认为它们已经排好序。所以我们需要做的，就是把前面取出的那个节点，接到剩余排好序的链表头节点前。

    /**
     * 方法二：递归
     * @param l1
     * @param l2
     * @return
     */
    public ListNode mergeTwoLists2(ListNode l1, ListNode l2) 
        // 基准情况
        if (l1 == null) return l2;
        if (l2 == null) return l1;

        // 比较头节点
        if (l1.value <= l2.value)
            // l1头节点比较小，直接提取出来，剩下的l1（l1头节点的next节点）和l2继续合并，接在l1后面
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        else 
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        
    

复杂度分析

时间复杂度：O(n + m)，其中 nn 和 m 分别为两个链表的长度。因为每次调用递归都会去掉 l1 或者 l2 的头节点（直到至少有一个链表为空），函数 mergeTwoList 至多只会递归调用每个节点一次。因此，时间复杂度取决于合并后的链表长度，即 O(n+m)。

空间复杂度：O(n + m)，其中 n 和 m 分别为两个链表的长度。递归调用 mergeTwoLists 函数时需要消耗栈空间，栈空间的大小取决于递归调用的深度。结束递归调用时 mergeTwoLists 函数最多调用 n+m 次，因此空间复杂度为 O(n+m)。

3. 删除链表的倒数第N个节点

3.1 题目说明

给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。

示例：

给定一个链表: 1->2->3->4->5, 和 n = 2.

当删除了倒数第二个节点后，链表变为 1->2->3->5.

说明：

给定的 n 保证是有效的。

3.2 分析

在链表中删除某个节点，其实就是将之前一个节点next，直接指向当前节点的后一个节点，相当于“跳过”了这个节点。

当然，真正意义上的删除，还应该回收节点本身占用的空间，进行内存管理。这一点在java中我们可以不考虑，直接由JVM的GC帮我们实现。

3.3 方法一：计算链表长度（二次遍历）

最简单的想法是，我们首先从头节点开始对链表进行一次遍历，得到链表的长度 L。

然后，我们再从头节点开始对链表进行一次遍历，当遍历到第 L-N+1 个节点时，它就是我们需要删除的倒数第N个节点。

这样，总共做两次遍历，我们就可以得到结果。

    /**
     * 方法一：计算链表长度（二次遍历）
     * @param head
     * @param n
     * @return
     */
    public ListNode removeNthFromEnd(ListNode head, int n)
        // 1.遍历链表，得到长度l
        int l = getLength(head);

        // 2.从前到后继续遍历，找到正数第l-n+1个元素
        // 定义一个哨兵节点，next指向头节点
        ListNode sentinel = new ListNode(-1);
        sentinel.next = head;

        ListNode curr = sentinel;
        for (int i = 0 ; i < l - n; i++)
            curr = curr.next;
        

        curr.next = curr.next.next;
        return sentinel.next;
    

    private static int getLength(ListNode head) 
        int length = 0;
        while (head != null)
            length++;
            head = head.next;
        
        return length;
    

3.4 方法二：利用栈

另一个思路是利用栈数据结构。因为栈是“先进后出”的，所以我们可以在遍历链表的同时将所有节点依次入栈，然后再依次弹出。

这样，弹出栈的第 n 个节点就是需要删除的节点，并且目前栈顶的节点就是待删除节点的前驱节点。这样一来，删除操作就变得十分方便了。

    /**
     * 方法二：计算链表长度（二次遍历）
     * @param head
     * @param n
     * @return
     */
    public ListNode removeNthFromEnd2(ListNode head, int n)

        // 2.从前到后继续遍历，找到正数第l-n+1个元素
        // 定义一个哨兵节点，next指向头节点
        ListNode sentinel = new ListNode(-1);
        sentinel.next = head;

        ListNode curr = sentinel;

        // 定义一个栈
        Stack<ListNode> stack = new Stack<>();

        // 将所有节点入栈
        // 入栈依次为 null、1、2、3、4、5
        while (curr != null)
            stack.push(curr);
            curr = curr.next;
        

        // 弹栈n次，假如n=2，出栈为5、4
        for (int i = 0 ; i < n; i++)
            stack.pop();
        

        // 栈顶元素为3，将3.next->5
        // （3.next->4.next->5）,则 3->5
        stack.peek().next = stack.peek().next.next;
        return sentinel.next;
    

复杂度分析

时间复杂度：O(L)，其中 L是链表的长度。我们压栈遍历了一次链表，弹栈遍历了N个节点，所以应该耗费O(L+N)时间。N <= L，所以时间复杂度依然是O(L)，而且我们可以看出，遍历次数比两次要少，但依然没有达到“一次遍历”的要求。

空间复杂度：O(L)，其中 L 是链表的长度。主要为栈的开销。

3.5 方法三：双指针（一次遍历）

我们可以使用两个指针 first 和 second 同时对链表进行遍历，要求 first 比 second 超前 N 个节点。

这样，它们总是保持着N的距离，当 first 遍历到链表的末尾（null）时，second 就恰好处于第L-N+1，也就是倒数第 N 个节点了。

    /**
     * 方法三：双指针（一次遍历）
     * @param head
     * @param n
     * @return
     */
    public ListNode removeNthFromEnd3(ListNode head, int n)

        // 1.从前到后继续遍历，找到正数第l-n+1个元素
        // 定义一个哨兵节点，next指向头节点
        ListNode sentinel = new ListNode(-1);
        sentinel.next = head;

        // 定义前后双指针
        ListNode first = sentinel, second = sentinel;

        // first先走n+1步
        for (int i = 0 ; i < n+1; i++)
            first = first.next;
        
        // first、second同时前进，当first变为null,second就是倒数第n+1个节点
        while (first != null)
            first = first.next;
            second = second.next;
        

        second.next = second.next.next;
        return sentinel.next;
    

复杂度分析

时间复杂度：O(L)，其中 L是链表的长度。这次真正实现了一次遍历。

空间复杂度：O(1)。