并行计算的量化模型及其在深度学习引擎里的应用
Posted OneFlow深度学习框架
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了并行计算的量化模型及其在深度学习引擎里的应用相关的知识,希望对你有一定的参考价值。

撰文|袁进辉
天下武功,唯快不破。怎么更快地训练深度学习模型是业界一直关注的焦点,业界玩家或开发专用硬件,或开发软件框架,各显神通。本文将介绍对深度学习计算效率最关键的一些基本定律,这有助于用户理解深度学习引擎的瓶颈在哪里以及如何解决这些挑战。
当然,这些定律在计算机体系结构的教材和文献中都可看到,譬如这本《计算机体系结构:量化研究方法(Computer Architecture: a Quantative Approach)》,但本文的价值在于有针对性地挑选最根本的几条定律,并结合深度学习引擎来理解。
1
关于计算量的假定
在研究并行计算的定量模型之前,我们先做一些设定。对于一个具体的深度学习模型训练任务,假设总的计算量V固定不变,那可以粗略认为只要完成V这个量级的计算,深度学习模型就完成训练。
GitHub这个页面(https://github.com/albanie/convnet-burden)罗列了常见CNN模型处理一张图片所需的计算量,需要注意的是,本页面列出的是前向阶段的计算量,在训练阶段还需要后向阶段的计算,通常后向阶段的计算量是大于前向计算量的。这篇论文(https://openreview.net/pdf?id=Bygq-H9eg)对训练阶段处理一张图片的计算量给出了一个直观的可视化结果:
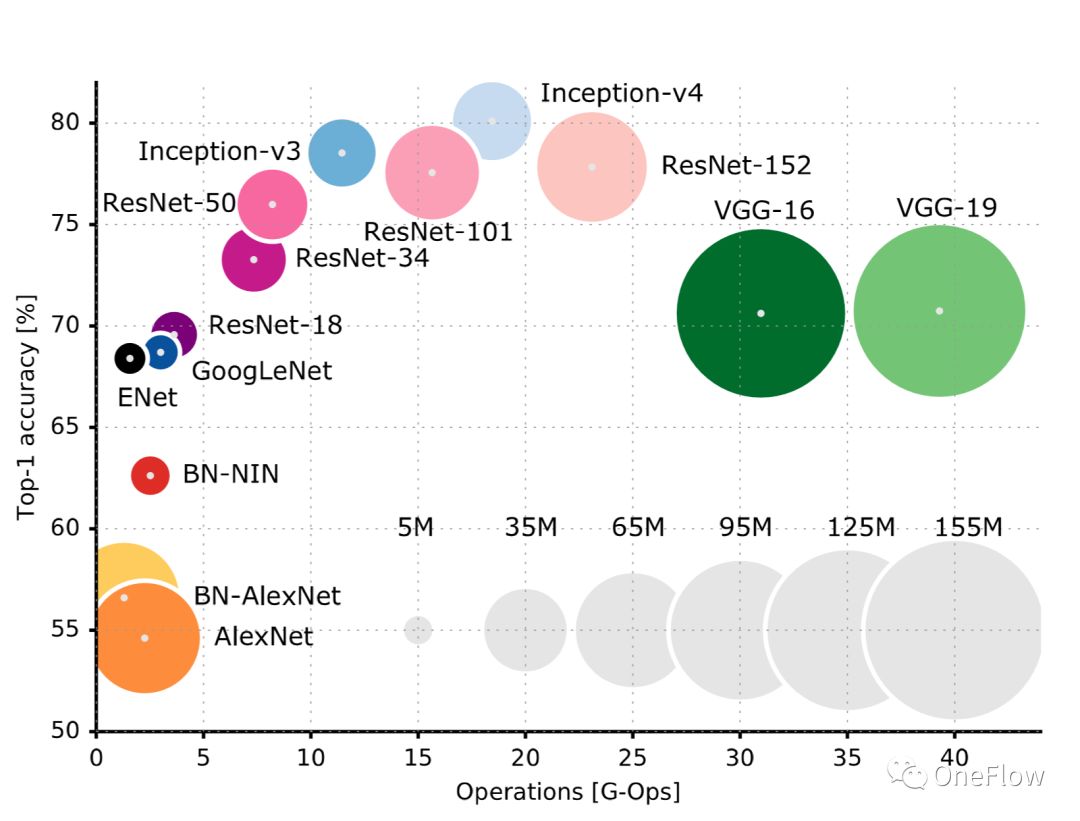
以ResNet-50为例,训练阶段处理一张224X224x3的图片需要8G-Ops (约80亿次计算),整个ImageNet数据集约有120万张图片,训练过程需要对整个数据集合处理90遍(Epochs),粗略估计,训练过程共需要(8*10^9) *(1.2*10^6)* 90 = 0.864*10^18次运算,那么ResNet-50训练过程的总计算量大约是10亿乘以10亿次运算,我们可以简单地认为,只要完成这些计算量就完成了模型运算。深度学习计算引擎的目标是以最短的时间完成这个给定的计算量。
2
关于计算装置的假定
本文仅限于下图所示的以处理器为中心的计算装置(Processor-centric computing),以内存为中心的计算(Processing in memory)装置在业界有探索,但还不是主流。
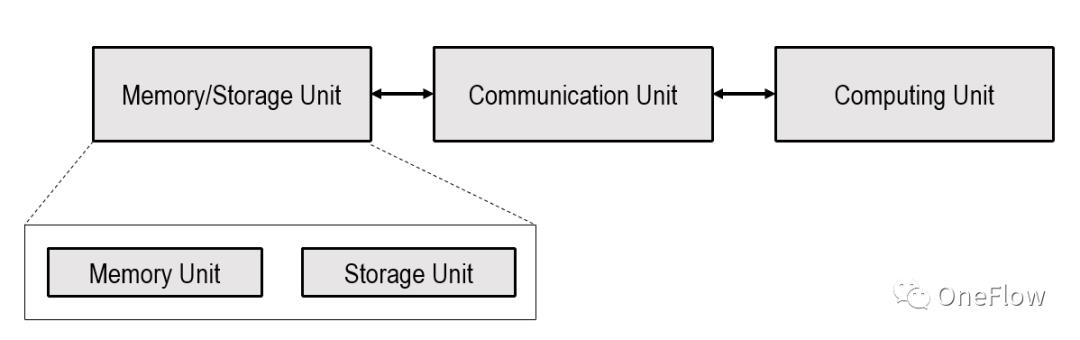
上图所示的计算装置中Computing Unit可以是通用处理器如CPU, GPGPU, 也可以是专用芯片如TPU等。如果Computing Unit是通用芯片,通常程序和数据都存储在Memory Unit,这也是现在最流行的冯诺依曼结构计算机。
如果Computing Unit是专用芯片,通常只有数据存储在Memory Unit。Communication Unit负责把数据从Memory Unit搬运给Computing Unit,完成数据加载(load),Computing Unit拿到数据后负责完成计算(数据的形式转换),再由Communication Unit把计算结果搬运到Memory Unit完成数据存储(Store)。
Communication Unit的传输能力通常用访存(Memory access)带宽beta表示,即每秒钟可以搬运的字节数,这通常和线缆数和信号的频率相关。Computing Unit的计算能力通常用吞吐率pi表示,即每秒钟可以完成的浮点计算次数(flops),这通常和计算单元上集成的逻辑运算器件个数及时钟频率有关。
深度学习引擎的目标是通过软硬件协同设计使得该计算装置处理数据的能力最强,即用最短的时间完成给定的计算量。
3
Roofline Model: 刻画实际计算性能的数学模型
一个计算装置执行一个任务时能达到的实际计算性能(每秒钟完成的操作次数)不仅与访存带宽beta以及计算单元的理论峰值pi有关,还和当前任务本身的运算强度(Arithemetic intensity,或Operational intensity)。
任务的运算强度定义为每字节数据需要的浮点计算次数,即Flops per byte。通俗地理解,一个任务运算强度小,表示Computing Unit在Communication Unit搬运的一个字节上需要执行的运算次数少,为了让Computing Unit在这种情况下处于忙碌状态,Communication Unit就要频繁搬运数据;
一个任务运算强度大,表示Computing Unit在Communication Unit搬运的一个字节上需要执行的运算次数多,Communication Unit不需要那么频繁地搬运数据就能使Computing Unit处于忙碌状态。
首先,实际计算性能不会超越计算单元的理论峰值pi。其次,假如访存带宽beta特别小,1秒钟仅能把beta个字节从内存搬运到Computing Unit,令I表示当前计算任务中每个字节需要的操作次数,那么beta * I 表示1秒钟内搬运过来的数据实际需要的操作次数,如果beta * I < pi,则Computing Unit就不会饱和,也表示Computing Unit的利用率低于100%。
Roofline model 就是一种根据访存带宽,计算单元峰值吞吐率,任务的运算强度三者关系来推断实际计算性能的数学模型。由David Patterson团队在2008年发表在Communications of ACM上(https://en.wikipedia.org/wiki/Roofline_model),是一种简洁优雅的可视化模型:
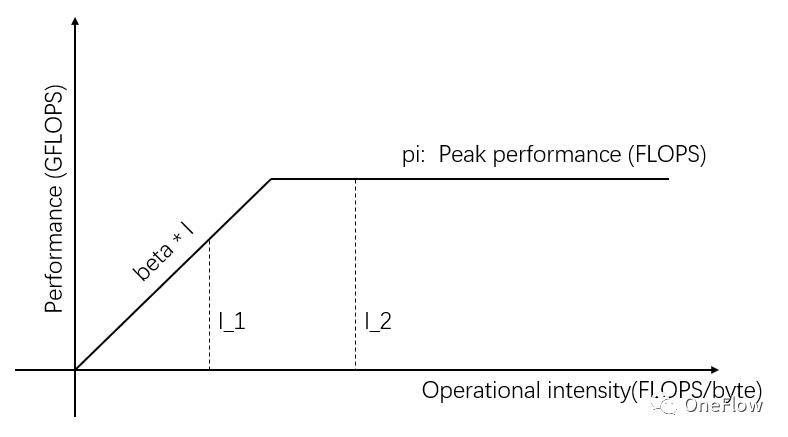
图1:Roofline Model
图1横轴的自变量表示不同任务的运算强度,即每字节需要的浮点运算次数。纵轴的因变量表示实际可达的计算性能,即每秒钟执行的浮点运算次数。上图展示了两个运算强度分别为I_1和I_2的任务能实际达到的计算性能,I_1的运算强度小于pi/beta,称为访存受限任务,实际计算性能beta * I_1低于理论峰值pi。
I_2的运算强度高于pi/beta,称为计算受限型任务,实际计算性能达到理论峰值pi,访存带宽仅利用了pi/(I_2*beta)。图中斜线的斜率为beta,斜线和理论峰值pi 水平线的交点称为脊点(Ridge point),脊点的横坐标是pi/beta,当任务的运算强度等于pi/beta时,Communication Unit和Computing Unit处于平衡状态,哪一个都不会浪费。
回顾深度学习引擎的目标“以最短的时间完成给定的计算量”,就要最大化系统的实际可达的计算性能。为了实现这个目标,有几种策略可用。
图1中的I_2是计算受限型任务,可以通过增加Computing Unit的并行度并进而提高理论峰值来提高实际计算性能,譬如在Computing Unit上集成更多的运算逻辑单元(ALU)。具体到深度学习场景,就是增加GPU,从一个GPU增加到几个GPU同时运算。
如图2所示,当在Computing Unit内增加更多的并行度后,理论峰值高于beta * I_2,那么I_2的实际计算性能就更高,只需要更短的时间就可以。
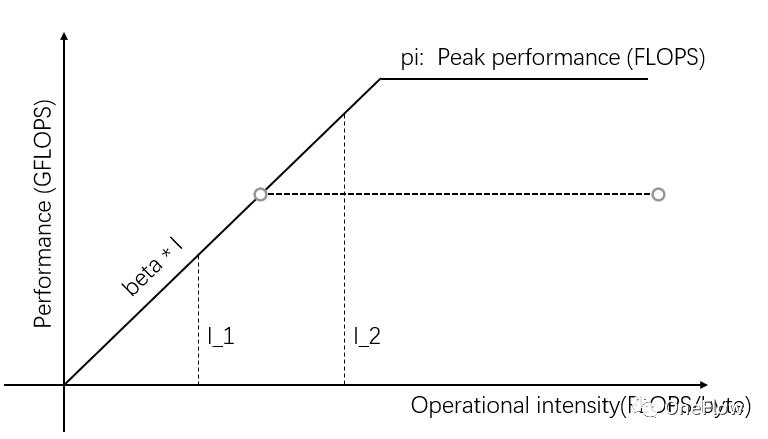
图2:提高Computing Unit的理论峰值来提高实际计算性能
图1中的I_1是访存受限型的任务,则可以通过改善Communication Unit的传输带宽来提高实际计算性能,提高数据供应能力。如图3所示,斜线的斜率表示Communication Unit的传输带宽,当斜线的斜率增大时,I_1由访存受限型任务变成计算受限型任务,实际计算性能得到提高。
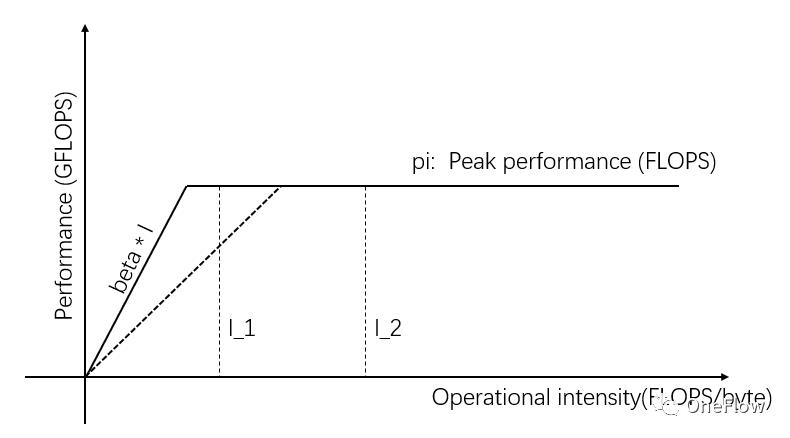
图3:提高Communication Unit的数据供应能力来提高实际计算性能
除了通过改善硬件的传输带宽或者理论峰值来提高实际计算性能外,还可以通过改善任务本身的运算强度来提高实际计算性能。同样的任务可以有多种不同的实现方式,不同实现方式的运算强度也存在差别。运算强度由I_1改造成超过pi/beta后,就变成计算受限型任务,实际计算性能达到pi,超过原来的beta*I_1。
在实际的深度学习引擎里,以上三种手段(提高并行度,改善传输带宽,使用运算强度更好的算法实现)都会用到。
4
Amdahl's Law: 如何计算加速比?
图2 的示例通过增加Computing Unit的并行度来提高实际计算性能,到底能把任务的执行时间缩短多少呢?这就是加速比问题,也就是效率提高了几倍。
为了讨论方便,(1)我们假设当前的任务是计算受限型,令I表示运算强度,即I*beta>pi。在把Computing Unit的运算单元增加s倍后,理论计算峰值是s * pi,假设该任务的运算强度I足够高,使得在理论峰值提高s倍之后仍是计算受限型,即I*beta > s*pi;(2)假设没有使用流水线,Communication Unit和Computing Unit总是顺序执行(后文我们将专门讨论流水线的影响)。让我们来计算一下任务执行效率提高了几倍。
在理论峰值是pi的初始情况下,1秒钟Communication Unit搬运了beta字节的数据,Computing Unit需要(I*beta)/pi 秒来完成计算。即在1+(I*beta)/pi 秒时间内完成了I*beta的计算,那么单位时间内可以完成(I*beta) / (1 + (I*beta)/pi) 的计算,假设总计算量是V,则一共需要t1=V*(1+(I*beta)/pi)/(I*beta) 秒。
通过增加并行度把理论计算峰值提高s倍之后,Communication Unit搬运beta字节的数据仍需要1秒钟,Computing Unit需要(I*beta)/(s*pi)秒来完成计算。假设总计算量是V,那么共需t2=V*(1+(I*beta)/(s*pi))/(I*beta)秒完成任务。
计算t1/t2即获得加速比:1/(pi/(pi+I*beta)+(I*beta)/(s*(pi+I*beta))),很抱歉这个公式比较难看,读者可以自己推导一下,比较简单。
在理论峰值是pi时,搬运数据花了1秒,计算花了(I*beta)/pi 秒,那么计算时间占的比例是 (I*beta)/(pi + I*beta),我们令p表示这个比例,等于(I*beta)/(pi + I*beta)。
把p代入t1/t2的加速比,可以得到加速比为1/(1-p+p/s),这就是大名鼎鼎的Amdahl's law(https://en.wikipedia.org/wiki/Amdahl%27s_law)。其中p表示原始任务中可以被并行化部分的比例,s表示并行化的倍数,则1/(1-p+p/s)表示获得的加速比。
让我们用一个简单的数字演算一下,假设Communication Unit搬运数据花了1秒钟,Computing Unit需要用9秒钟来计算,则p=0.9。假设我们增强Computing Unit的并行度,令其理论峰值提高3倍,即s=3,则Computing Unit只需要3秒钟就可以完成计算,那么加速比是多少呢?利用Amdahl's law可以得知加速比是2.5倍,加速比2.5小于Computing Unit的并行度倍数3。
我们尝到了增加Computing Unit并行度的甜头,能不能通过进一步提高并行度s来获得更好的加速比呢?可以。譬如令s=9,那么我们可以获得5倍加速比,可以看到提高并行度的收益越来越小。
我们能通过无限提高s来提高加速比吗?可以,不过越来越不划算,试想令s趋于无穷大(即令Computing Unit理论峰值无限大),p/s就趋于0,那么加速比最大是1/(1-p)=10。
只要系统中存在不可并行的部分(Communication Unit),加速比不可能超过1/(1-p)。
实际情况可能比加速比上限1/(1-p)要更差一些,因为上述分析假设了运算强度I无穷大,而且在增加Computing Unit并行度时,通常会使得Communication Unit的传输带宽下降,就使得p更小,从而1/(1-p)更大。
这个结论令人很悲观,即使通信开销(1-p)只占0.01,也意味着无论使用多少并行单元,成千上万,我们最大只能获得100倍的加速比。有没有办法让p尽可能接近1,也就是1-p趋近于0,从而提高加速比呢?有一枚灵丹妙药:流水线。
5
Pipelining: 灵丹妙药
在推导Amdahl's law时,我们假设了Communication Unit和Computing Unit串行工作,总是先令Communication Unit搬运数据,Computing Unit再做计算,计算完成再令Communication Unit搬运数据,再计算,如此循环往复。
能不能让Communication Unit和Computing Unit同时工作,一边搬运数据一边计算呢?如果Computing Unit每计算完一份数据,就立刻可以开始计算下一批数据,那么p就几乎是1,无论并行度s提高多少倍,都能获得线性加速比。让我们研究一下什么条件下可以获得线性加速比。
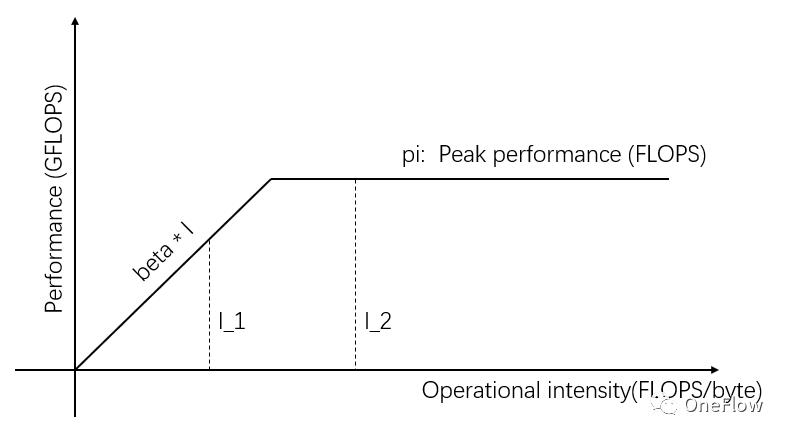
图4:(同图1)Roofline Model
图4中的I_1是通信受限型任务,1秒钟Communication Unit可以搬运beta字节的数据,处理这beta字节Computing Unit需要的计算量是beta*I_1次操作,理论计算峰值是pi,一共需要(beta*I_1)/pi秒完成计算。
对于通信受限型任务,我们有beta*I_1<pi,所以Computing Unit的计算时间是小于1秒的。这也就意味着不到1秒的计算却需要花1秒钟的时间搬运数据,那么计算时间就无法掩盖住数据搬运时间,p最大可以做到(beta*I_1)/pi,加速比最大是1/(pi-beta*I_1)。
图4中的I_2是计算受限任务,1秒钟Communication Unit可以搬运beta字节的数据,处理这beta字节Computing Unit需要的计算量是beta*I_2次操作,理论计算峰值是pi,一共需要(beta*I_2)/pi秒完成计算。对于计算受限型任务,我们有beta*I_2>pi,所以Computing Unit的计算时间是大于1秒的。
这也就意味着,每花1秒钟搬运的数据需要好几秒才能计算完,在计算的时间内有充足的时间去搬运下一批数据,也就是计算时间能掩盖住数据搬运时间,p最大是1,只要I是无穷大,加速比就可以无穷大。
使得Communication Unit和Computing Unit重叠工作的技术叫流水线(Pipelinging: https://en.wikipedia.org/wiki/Pipeline_(computing))。是一种有效地提高Computing Unit利用率和提高加速比的技术。
6
并行计算的量化模型对深度学习引擎的启发
上文讨论的各种量化模型对深度学习引擎研发同样适用,譬如对于计算受限型任务,可以通过增加并行度(增加显卡)来加速;即使是使用同样的硬件设备,使用不同的并行方法(数据并行,模型并行或流水线并行)会影响到运算强度I,从而影响实际计算性能;分布式深度学习引擎包含大量的通信开销和运行时开销,如何减小或掩盖这些开销对于加速效果至关重要。
在Processor-centric计算装置的视角下理解基于GPU训练深度学习模型,读者可以思考一下怎么设计深度学习引擎来获得更好的加速比。
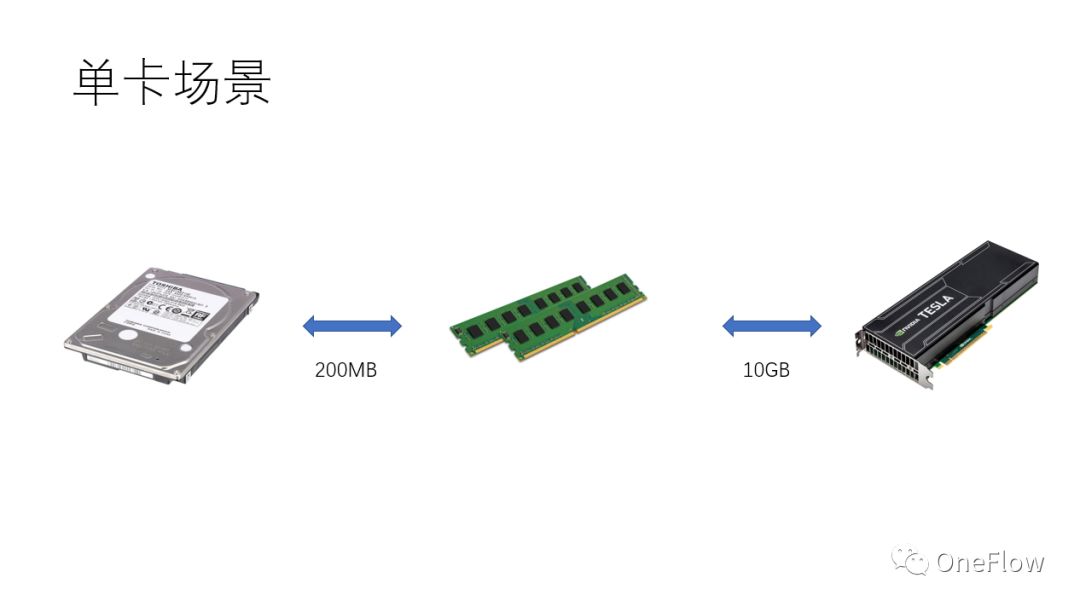
在单机单卡情况下,只需要做好数据搬运和计算的流水线,就可以做到GPU 100%的利用率。实际计算性能最终取决于底层矩阵计算的效率,也就是cudnn的效率,理论上各种深度学习框架在单卡场景不应该存在性能差距。
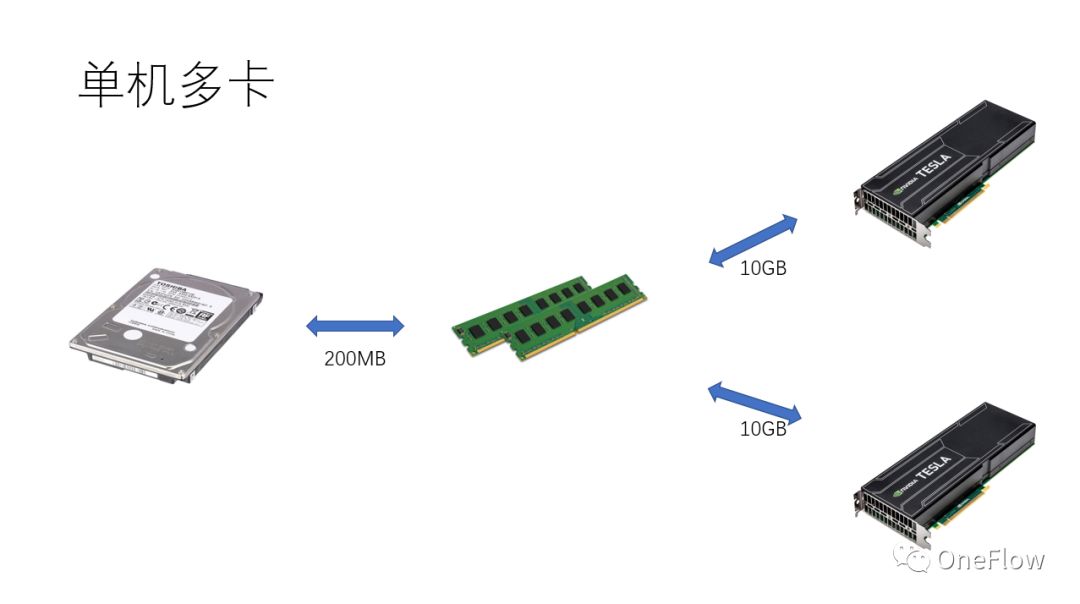
如果想在同一台机器内部通过增加GPU来获得加速,与单卡场景相比,增加了GPU之间数据搬运的复杂性,不同的任务切分方式可能会产生不同的运算强度I(譬如对卷积层适合做数据并行,对全连接层适合模型并行)。除了通信开销,运行时的调度开销也会影响加速比。
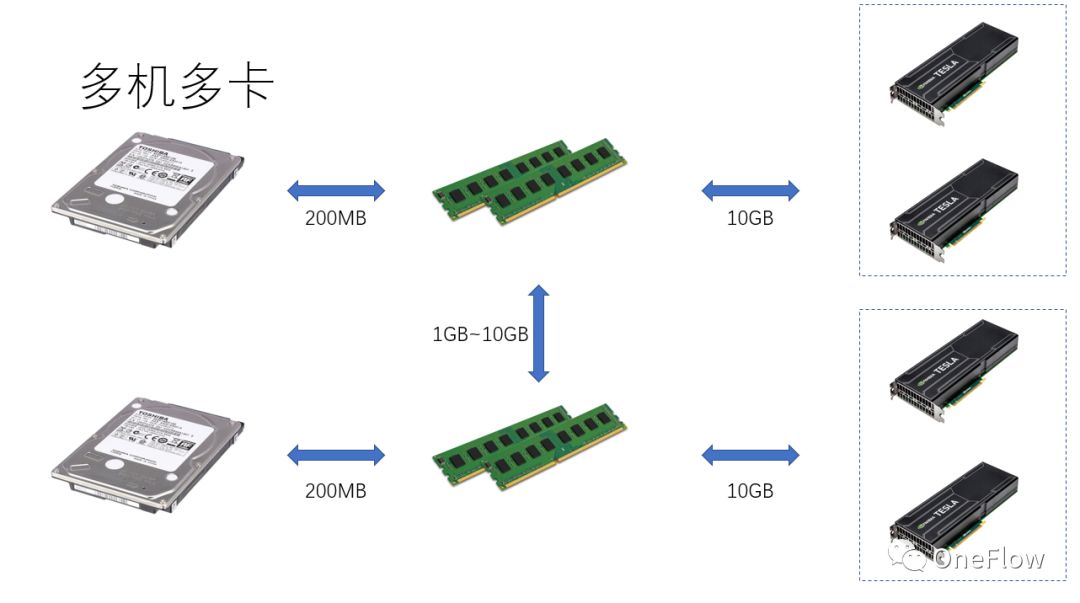
多机多卡场景,GPU之间数据搬运的复杂性进一步提高,机器之间通过网络搬运数据的带宽一般低于机器内部通过PCIe搬运数据的带宽,这意味着并行度提高了,可数据搬运带宽降低了,代表着Roofline model中斜线的斜率变小了,CNN这种适合数据并行的场景通常意味着比较高的运算强度I,而还有一些模型譬如RNN/LSTM,运算强度I就小很多,这也意味着流水线中的通信开销更难以掩盖了。
7
总结
有用过分布式深度学习引擎的读者应该对软件框架的加速比有切身的体会,基本上,卷积神经网络这种适合数据并行(运算强度I比较高)的模型通过增加GPU来加速的效果还是比较令人满意的,然而,还有很大一类神经网络使用模型并行的运算强度才更高一点,而且即使使用模型并行,其运算强度也远低于卷积神经网络,对于这些应用如何通过增加GPU并行度来获得加速是业界尚未解决的难题。
在之前的深度学习评测中,甚至发生了使用多GPU训练RNN速度比单个GPU还要慢的情况(https://rare-technologies.com/machine-learning-hardware-benchmarks/)。无论使用什么技术解决深度学习引擎的效率问题,万变不离其宗,为了提高加速比,都是为了减小运行时开销,选择合适的并行模式来提高运算强度,通过流水线掩盖通信开销,也都在本文描述的基本定律涵盖的范围之内。
(本文完成于2018年初,文中所举例子已比较陈旧,但不影响原理的阐释。)
其他人都在看
点击“阅读原文”,欢迎体验OneFlow v0.7.0

以上是关于并行计算的量化模型及其在深度学习引擎里的应用的主要内容,如果未能解决你的问题,请参考以下文章