Java算法 -- 二分查找：查找目标元素最左的位置和最右的位置局部最小值问题求解

Posted 2022-06-20 CodeJiao

1. 二分查找

二分查找也是一种在数组中查找数据的算法。它只能查找已经排好序的数据。二分查找通过比较数组中间的数据与目标数据的大小，可以得知目标数据是在数组的左边还是右边。因此，比较一次就可以把查找范围缩小一半。重复执行该操作就可以找到目标数据，或得出目标数据不存在的结论。

二分查找的代码：

    /**
     * 二分查找算法
     *
     * @param arr    待查找的数组
     * @param target 目标元素
     * @return 目标元素下标，如不存在返回-1
     * @throws Exception 参数异常
     */
    public int binarySearch(int[] arr, int target) throws Exception 
        if (arr == null || arr.length == 0) 
            throw new Exception("参数错误！");
        
        int left = 0, right = arr.length - 1;
        while (left <= right) 
            int middle = left + ((right - left) >> 1);
            if (arr[middle] == target) 
                return middle;
             else if (arr[middle] > target) 
                right = middle - 1;
             else 
                left = middle + 1;
            
        
        return -1;
    

如果有多个目标元素，上面这个元素无法保证目标元素的相对位置，比如保证可以找到第一个目标元素和最后一个目标的索引。

---

1.1 有序数组中找到>=target最左的位置

    public static int binarySearchLeft(int[] arr, int target) throws Exception 
        if (arr == null || arr.length == 0) 
            throw new Exception("参数错误！");
        
        int left = 0, right = arr.length - 1, result = -1;
        while (left <= right) 
            int middle = left + ((right - left) >> 1);
            if (arr[middle] >= target) 
                result = middle;
                right = middle - 1;
             else 
                left = middle + 1;
            
        
        return result;
    

测试代码：

---

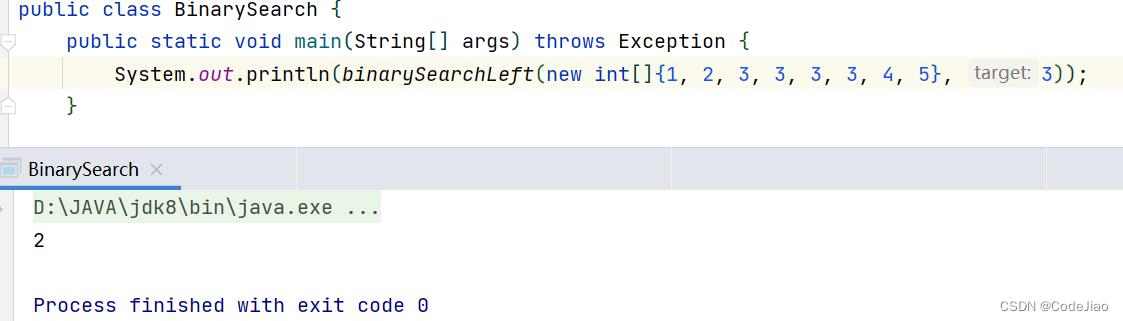
1.2 有序数组中找到<=target最右的位置

    public static int binarySearchRight(int[] arr, int target) throws Exception 
        if (arr == null || arr.length == 0) 
            throw new Exception("参数错误！");
        
        int left = 0, right = arr.length - 1, result = -1;
        while (left <= right) 
            int middle = left + ((right - left) >> 1);
            if (arr[middle] <= target) 
                result = middle;
                left = middle + 1;
             else 
                right = middle - 1;
            
        
        return result;
    

测试代码：

---

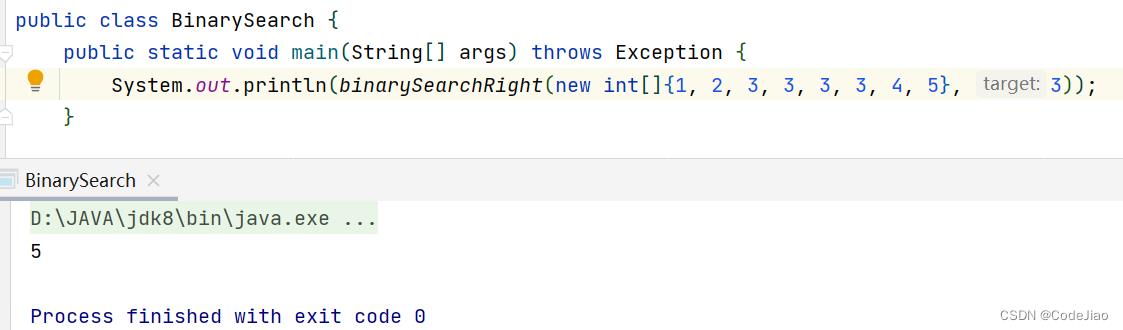
1.3 局部最小值

假设现在有一个整型数组nums，他有个特点：相邻的元素不相同。（不一定有序）

现在我们要查找这个数组的的一个局部最小值。

那么什么是局部最小值呢？假设nums的长度为n。

• 对于边界来说，如果nums[0] < nums[1]，则nums[0]是一个局部最小。如果nums[n-1] < nums[n-2]，则nums[n-1]是一个局部最小。
• 对于非边界来说，如果i ∈ [i,n-2] ，并且nums[i] < nums[i+1] && nums[i] < nums[i-1]，则nums[i]是一个局部最小。

我们来分析一下怎么用Java代码来实现求局部最小值。

1. 刚开始就分析边界情况。
2. 如果不存在边界情况，则nums[0] > nums[1] && nums[n-1] > nums[n-2]，这在数学上可以表现为：
   
   因为左边是减函数，右边是增函数，所以索引[0,n-1]之间的元素一定存在一个局部最小值。这时候我们可以继续二分查找。
   

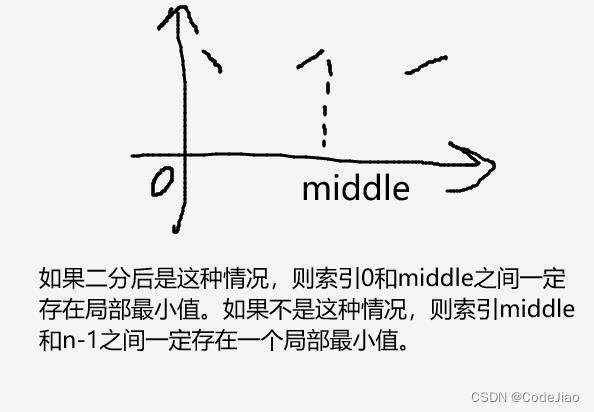
查找局部最小值的Java代码如下：

    /**
     * 获取局部最小值
     *
     * @param arr 待查找的数组,  相邻元素不相等
     * @return 局部最小值的索引, 查找不到返回-1
     */
    public static int getRecentMinNum(int[] arr) throws Exception 
        if (arr == null || arr.length == 0) 
            throw new Exception("参数错误！");
        
        int length = arr.length;
        if (length == 1) 
            return 0;
        
        if (arr[0] < arr[1]) 
            return 1;
        
        if (arr[length - 1] < arr[length - 2]) 
            return length - 1;
        

        int left = 0, right = length - 1;
        // 只有当left和right之间大于等于3个元素时才继续二分, 即最小剩下left,right-1,right-2 3个元素
        // 这样做的目的是保证 arr[middle - 1] 不会出现数组下标越界的情况
        while (left < right - 1) 
            int middle = left + ((right - left) >> 1);
            if (arr[middle] < arr[middle - 1] && arr[middle] < arr[middle + 1]) 
                return middle;
             else if (arr[middle] > arr[middle - 1]) 
                right = middle - 1;
             else 
                left = middle + 1;
            
        
        // 到了这一步, 数组一定只剩下2个元素待比较了
        return arr[left] < arr[right] ? left : right;
    

测试：

---

---

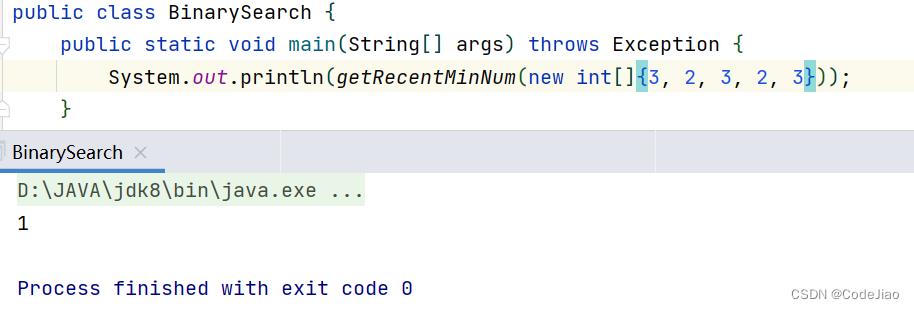
开发者涨薪指南 48位大咖的思考法则、工作方式、逻辑体系