信号与系统笔记(4-4)复频域分析
Posted AXYZdong
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了信号与系统笔记(4-4)复频域分析相关的知识,希望对你有一定的参考价值。
Author:AXYZdong
自动化专业 工科男
有一点思考,有一点想法,有一点理性!
CSDN@AXYZdong
文章目录
一、微分方程变换解

解:微分方程两边取拉氏变换,可得:
( s 2 + 5 s + 6 ) Y ( s ) − s y ( 0 − ) − y ′ ( 0 − ) − 5 y ( 0 − ) = ( 2 s + 10 ) F ( s ) (s^2+5s+6)Y(s)-sy(0_-)-y'(0_-)-5y(0_-)=(2s+10)F(s) (s2+5s+6)Y(s)−sy(0−)−y′(0−)−5y(0−)=(2s+10)F(s)
整理:
Y ( s ) = s + 6 s 2 + 5 s + 6 + 2 s + 10 s 2 + 5 s + 6 ⋅ F ( s ) Y(s)=\\fracs+6s^2+5s+6+\\frac2s+10s^2+5s+6\\cdot F(s) Y(s)=s2+5s+6s+6+s2+5s+62s+10⋅F(s)
故: Y X ( s ) = s + 6 s 2 + 5 s + 6 = 4 s + 2 + − 3 s + 3 , Y f ( s ) = 2 s + 10 s 2 + 5 s + 6 = − 6 s + 2 + 2 s + 3 + 4 s + 1 Y_X(s)=\\fracs+6s^2+5s+6=\\frac4s+2+\\frac-3s+3,Y_f(s)=\\frac2s+10 s^2+5s+6=\\frac-6s+2+\\frac2s+3+\\frac4s+1 YX(s)=s2+5s+6s+6=s+24+s+3−3,Yf(s)=s2+5s+62s+10=s+2−6+s+32+s+14
零状态响应: y f ( t ) = ( 2 e − 3 t + 4 e − t − 6 e − 2 t ) ϵ ( t ) y_f(t)=(2e^-3t+4e^-t-6e^-2t)\\epsilon(t) yf(t)=(2e−3t+4e−t−6e−2t)ϵ(t)
零输入响应: y X ( t ) = ( 4 e − 2 t − 3 e − 3 t ) ϵ ( t ) y_X(t)=( 4e^-2t-3e^-3t)\\epsilon(t) yX(t)=(4e−2t−3e−3t)ϵ(t)
全响应: y ( t ) = ( − e − 3 t + 4 e − t − 2 e − 2 t ) ϵ ( t ) y(t)=(-e^-3t+4e^-t-2e^-2t)\\epsilon(t) y(t)=(−e−3t+4e−t−2e−2t)ϵ(t)
二、系统函数
系统函数定义为:
H
(
s
)
=
Y
f
(
s
)
F
(
s
)
=
B
(
s
)
A
(
s
)
H(s)=\\fracY_f(s)F(s)=\\fracB(s)A(s)
H(s)=F(s)Yf(s)=A(s)B(s)
它只与系统的结构、元件的参数有关,而与激励、初始状态无关。
y
f
(
t
)
=
h
(
t
)
∗
f
(
t
)
⟶
Y
f
(
s
)
=
L
[
h
(
t
)
]
F
(
s
)
y_f(t)=h(t)*f(t) \\longrightarrow Y_f(s)=\\mathcalL[h(t)]F(s)
yf(t)=h(t)∗f(t)⟶Yf(s)=L[h(t)]F(s)

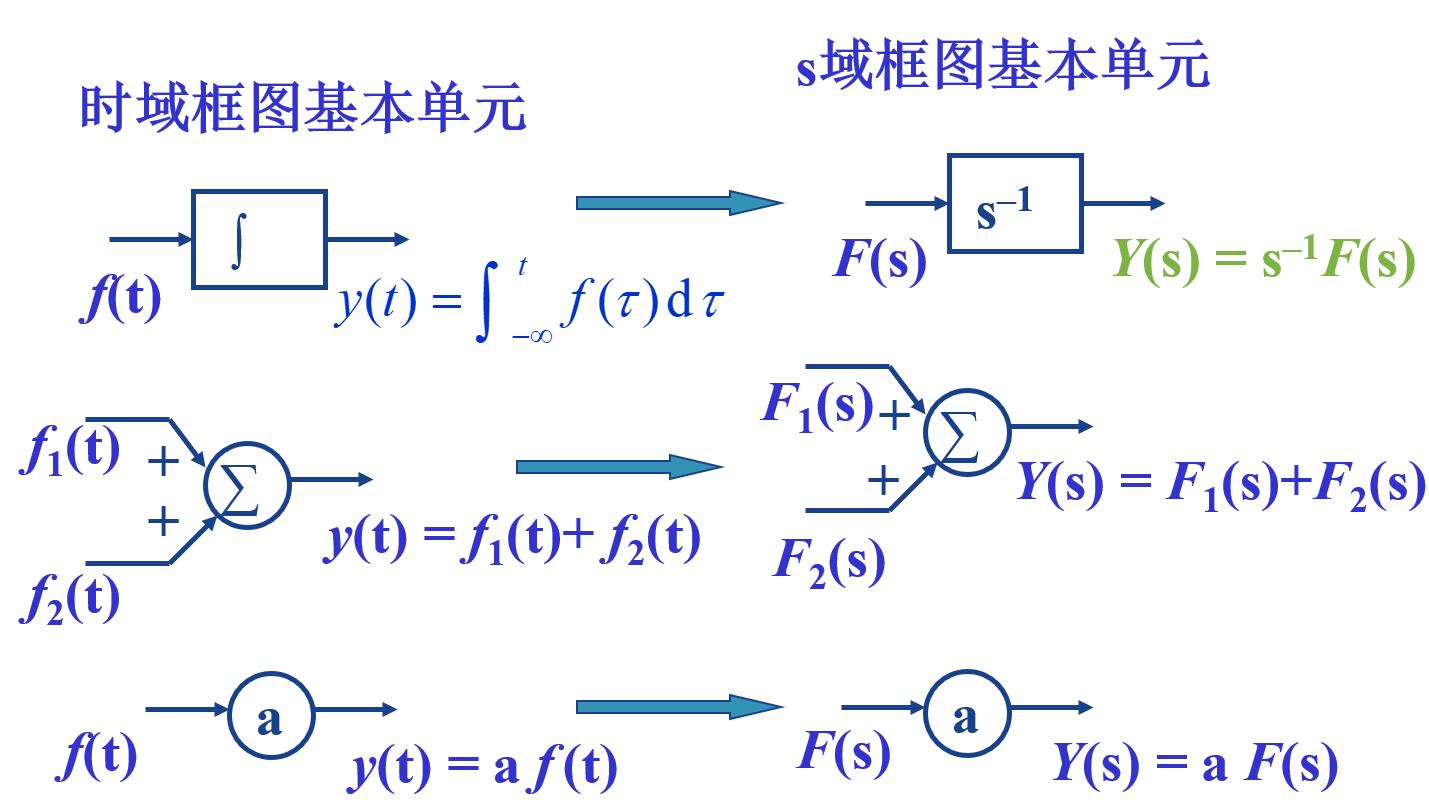
三、系统的s域框图
例:
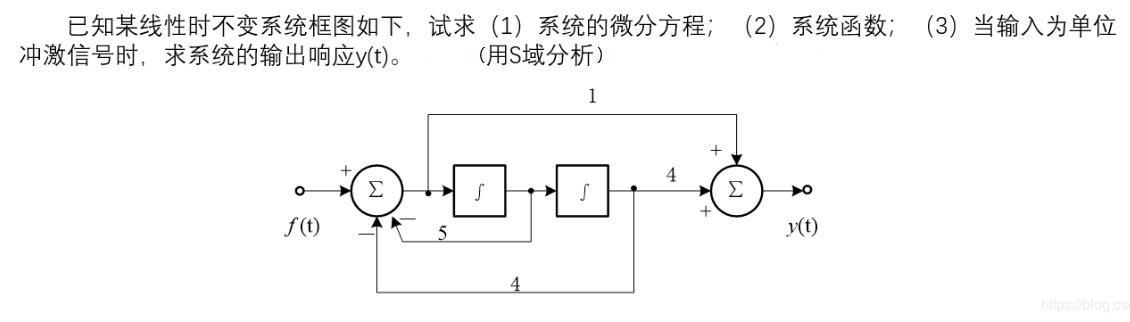
解:设左边加法器输出为: X ( s ) X(s) X(s)
则: X ( s ) = F ( s ) − 5 s − 1 X ( s ) − 4 s − 2 X ( s ) X(s)=F(s)-5s^-1X(s)-4s^-2X(s) X(s)=F(s)−5s−1X(s)−4s−2X(s)
Y ( s ) = X ( s ) + 4 s − 2 X ( s ) Y(s)=X(s)+4s^-2X(s) Y(s)=X(s)+4s−2X(s)
可得: X ( s ) = s 2 s 2 + 5 s + 4 F ( s ) X(s)=\\fracs^2s^2+5s+4F(s) X(s)=以上是关于信号与系统笔记(4-4)复频域分析的主要内容,如果未能解决你的问题,请参考以下文章信号与线性系统综合实验 一、实验目的 1、掌握连续时间信号与系统的时域、频域综合分析方法;
