论文阅读查询搜索中的安全和效率权衡（ACM 10.1145）

Posted 2022-05-19 囚生CY

英文标题: Privacy and Efficiency Tradeoffs for Multiword Top K Searchwith Linear Additive Rank Scoring
中文标题: 具有线性累和排序评分的多单词TopK搜索的隐私性与效率性权衡
论文下载地址(免费): https://dl.acm.org/doi/10.1145/3178876.3186084

序言

1. 密码学11周结课, 差不多期中就要做汇报, 找了一篇跟查询安全有关的ACM报告, 主要感觉跟自然语言处理领域能搭得上边, 之前软件工程那块也是找了个语义WEB相关的内容, 都是具有很高关联性的技术点;

2. 这篇论文要解决的问题本质就是如何让服务器在尽可能少地知道用户查询的关键词以及搜索文档库所包含的任何信息的情况下, 还能够提供给用户一个非常完美的搜索结果排序;

3. 这看起来强人所难, 但是事实上不论是你在百度搜索引擎还是在其他网站上进行表单提交, 一般来说, 在比较正规安全的网络架构下, 服务器接收到数据都是经过加密处理的, 存在数据库里的信息大都也是加密后的结果, 服务器往往只能在加密过的信息上直接进行处理, 因为解密通常需要付出很多额外的空间和时间开销, 会极大地影响服务器性能和用户使用体验;

4. 本质上并不可能在安全和效率上同时取得最优, 因此总是要牺牲一些以达到一个折衷, 这似乎是句废话, 但是这篇论文的确给出了一个相当创新的解决方案;

5. 以下的提要基本上是对原文的完整翻译, 机翻的效果非常差, 笔者因为不太熟悉这个领域基本上是一个字一个字抠出来的, 虽然很蠢, 但是应该说这样做很有助于对文章的深入了解; 论文的下载链接已经在前文中给出, 有兴趣的朋友可以自行下载阅读英文原版, 理解起来可能会更好;

目录

• 序言
• • 摘要
  • 第一节 引入与相关工作 INTRODUCTION AND RELATED WORK
  • 第二节 问题定义与设计考虑 PROBLEM DEFINITION AND DESIGN CONSIDERATIONS
  • 第三节 服务端部分排序 SERVER-SIDE PARTIAL RANKING
  • 第四节 索引与查询处理 INDEXING AND QUERYPROCESSING
  • 第五节 评估 EVALUATION
  • 第六节 结束语 CONCLUDING REMARKS
  • 附录A 隐私分析 PRIVACY ANALYSIS
  • 参考文献
  • 附录B 图表

摘要

本文提出一个用于在中等尺寸(modest-sized)的云数据集上对top-K的关键词搜索进行高效排序的私有排序方案(private ranking schema), 这种私有排序方案是以线性递增的得分函数来确定的; 通过提出单轮C/S(client-server)协同, 服务端基于带随机掩码(masks)的盲目特征(blinded feature)权重进行部分排序, 这种schema在私有性与效率间追求平衡(strike for tradeoff); 客户端的预处理包括带有分块发布的查询分解, 以促进更早的范围交叉(earlier range intersection)和对服务端键值存储的快速访问; 服务端的查询处理通过以下方式处理特征向量稀疏性可选的特征匹配, 并启用与查询相关的块级随机掩码进行结果过滤, 以产生许多同样的用于查询匹配的文档; 本文提供了有关索引的详细信息和运行时联合查询处理(conjunctive query processing), 并提供一个评价以评估这个schema的准确性, 效率和隐私权衡(privacy tradeoff), 并通过五个不同尺寸的数据集实现此方案;

---

第一节 引入与相关工作 INTRODUCTION AND RELATED WORK

1. 研究背景:

• 云上的敏感数据规模激增, 对于用户来说在采用基于云的数据服务(包括关键词搜索)时, 隐私性保全是一个关键因素;
• 云服务器一般被认为是诚实但好奇的(honest-but-curious): 指服务器诚实地执行协议规范(protocal specification)和托管程序(hosted program), 但是服务器可能会在执行过程中或通过调查托管数据来观察和推断隐私数据;
• 为了处理这种服务器, 可搜索的加密(searchable encryption)会被用来实现隐私保全服务器侧查询匹配, 如用单个关键词, 使用OXT协议的联合多词, 或者分隔多词查询匹配;
• 包括OXT在内的研究不支持排序, 因为同时取得高效和安全是很难的topK排名很难, 所以这是一个公开的研究问题;

2. 问题难点:

• 实施服务器端隐私保全的topK排名的主要挑战在于:
  • 一方面, 先进的排序算法通常涉及基于原始特征(raw features, 详见第二节)的算术计算, 而通过加密隐藏的特征信息阻碍服务器进行高效的评分与结果比较;
  • 另一方面, 不加密的特征值(feature values)可能会导致受到隐私攻击(privacy attacks);
• 同态加密(Homomorphic encryption)是一种可以用来加密数据同时使得服务器可以在不解密底层数据的情况下进行算术计算;
  • 比如给定特征值(feature values)$f_1$和$f_2$, 服务器使用同态加密$E$就可以只通过$E(f_1)$和$E(f_2)$的值计算得到$E(f_1+f_2)$的值, 而无需知道$f_1$和$f_2$确切是多少;
  • 但是这样的schema在涉及大量数据时仍然不是计算可行的(computationally feasible), 因为此时乘法与加法极慢, 更不用说用同态加密计算评分来比较两个结果的能力了;
    • 比如同态加密不允许在服务器上高效比较$f_1+f_2$与$f_1^{\prime }+f_2^{\prime }$, 即使可以安全的计算$E(f_1+f_2)$和$E(f_1^{\prime }+f_2^{\prime })$的值;
  • 备注: 同态加密见[affliation.md]
• 次序保全加密(order-preserving encryption)支持在不解密的情况下高效比较两个加密结果, 但是它又不支持在不解密的情况下进行加法与乘法;
  • 备注: 保序加密见[affliation.md]
• 另一个挑战在于先进的排序会考虑许多特征, 特征向量通常是稀疏的(有很多零元), 直接存储零元会导致空间使用激增, 但使用压缩数据结构来存储又可能会泄露关于索引的统计信息(可能有恰当的防护可以使得不泄露), 这也许会导致泄露滥用攻击(leakage-abuse attacks);

3. 前人的研究:

• 关于基于相似性的安全排序(similarity-based secure ranking)的工作中, 会将每个基于TF-IDF的特征向量转化为两个随机向量;

  • 备注: 这里的两个随机向量理解为可能就是TF和IDF吧; 关于TF-IDF见[affliation.md]

• 索引构架通过乘以带有秘密矩阵(secret matrices)的特征向量, 建立前向索引;

  • 备注: 正排索引是从文档角度来找其中的单词，表示每个文档(用文档ID标识)都含有哪些单词, 以及每个单词出现了多少次(词频)及其出现位置(相对于文档首部的偏移量), 所以每次搜索都是遍历所有文章;

• 线上查询处理将给定的查询向量进行矩阵乘法变换, 然后获得变换后的查询向量关于所有加密文档向量的点相似度(dot similarity), 这个过程的时间复杂度是$O(T^2+DT)$, 其中$D$是文档的数量, $T$是字典的规模;

  • 备注: 复杂度$O(T^2+DT)$可以理解, 文档可以表示成一个字典维度的向量, 每个位置是单词出现的次数, 因此比较单词和文档将有$O(DT)$复杂度(计算点积有$DT$次乘法), 而$O(T^2)$复杂度猜测是需要预先计算不同单词之间相似度;

• 为了扩展这个模型以考虑包括单词对(word pairs)在内的邻近特征(proximity features), 参数$T$会变得非常大;

• 倒排索引并不可能, 因为线下与线上的带随机的矩阵变换会生成密度特征(dense feature)和查询向量, 存储索引的成本会变成$O(DT)$的空间复杂度;

  • 参考文献45与48使用了这种矩阵变换, 同时考虑多用户数据所有权(multiuser data ownership)和动态文档更新(dynamic document update);
  • 备注:
    • 倒排索引是从单词角度找文档, 标识每个单词分别在那些文档中出现(文档ID), 以及在各自的文档中每个单词分别出现了多少次(词频)及其出现位置(相对于该文档首部的偏移量);
    • 这是正向索引
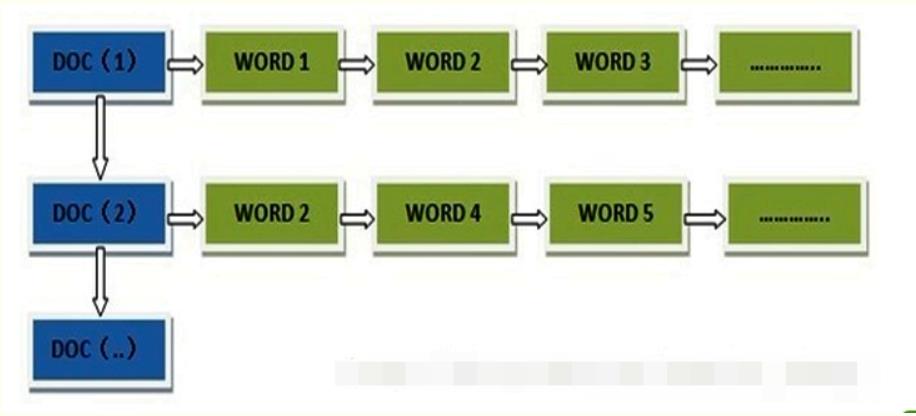
    • 这是逆向索引
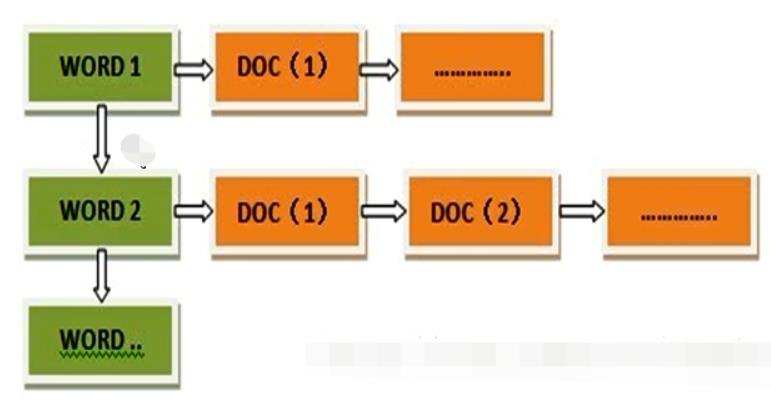
    • 直观上倒排索引更适合于排序, 但是这里提到倒排索引不可行, 原因似乎是空间占用, 但是前向索引并不能减少空间占用, 没有太搞明白;

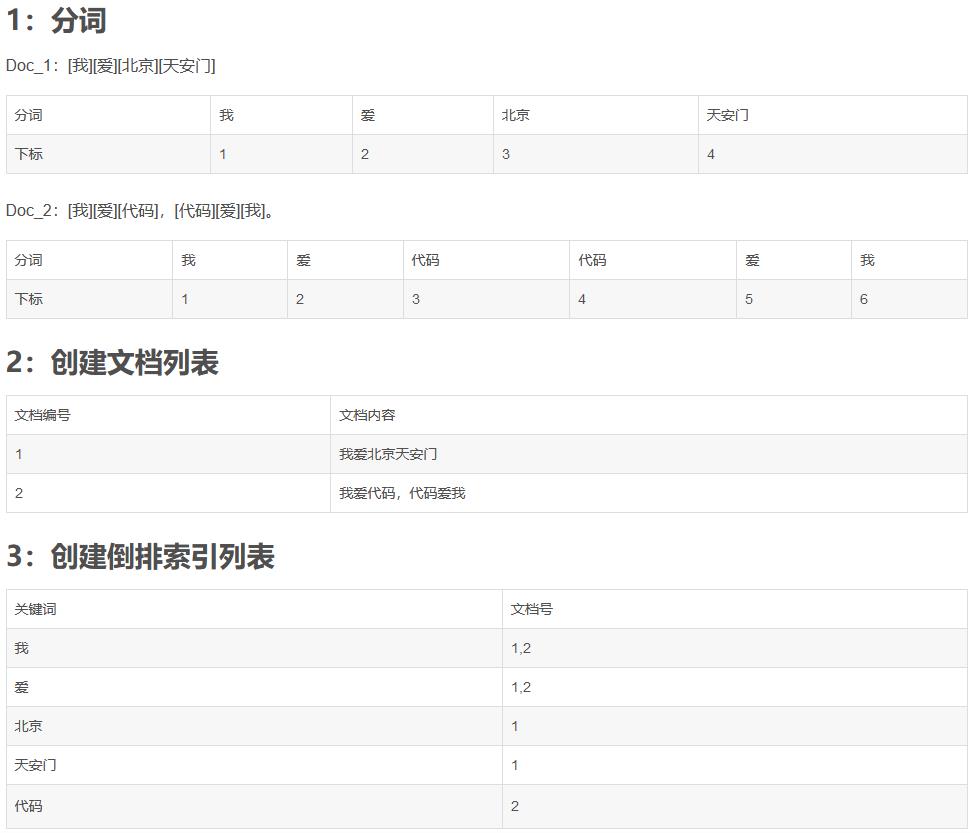
• 参考文献13, 32, 40中用于测试的数据集很小, 只有几千个文档或项目, 不用倒排索引的搜索成本很高导致这些文献提供的方法无法用于处理稍大一些的数据集;

4. 本文的研究:

• 综上所述似乎开发一个完全安全的, 无需诉诸重量级的密码学如功能加密(functional encryption)方法的排序schema是难以置信的, 因为实际生产中要求高响应速度, 服务器主机的算法必须部署折衷的轻量级方案来计算排名分数和选择结果;
• 本文用于解决这个私有排序问题的策略是利用以前的可搜索加密(searchable encryption)研究并在制定有效schema时进行折衷平衡, 使得有限的信息泄露到服务器;
• 本文采用了一个C/S协同的方法, 服务器执行高效匹配, 累积评分, 部分排序, 客户端执行查询预处理和最后的topK结果的选择;
• 本文设计仅仅使用一轮的C/S通信, 因为C/S多轮的活跃通信会导致高得多的通信成本与响应潜伏(response latency);
• 本文假设客户端拥有一个数据集, 将云上对应的索引设置为通过客户端可搜索的;
  • 原文: We assume that a client owns a dataset and places the corresponding index on the cloud to be searchable by the client.
  • 备注: 应该意思是客户端可以访问服务端的文档索引吧;
• 本文不考虑文档存在多用户所有权(文献48)的情况, 并假设云上的索引可以被周期性的更新, 但不考虑动态索引更新(dynamic index update, 文献30与35);
  • 备注: 每个文档隶属于单个用户, 动态索引更新简而言之是通过增加新的补充索引来反映新近的修改, 而不是直接重写整个倒排索引; 每一个倒排索引都会被轮流查询到$\to$从最早的开始$\to$查询完后再对结果进行合并; 这里应该是倒排索引总是会全局更新;
• 文献4和5研究了查询争夺(query scrambling), 旨在私网搜索(private web)的发布查询(issuing queries)中保护用户隐私, 但是他们假设服务器拥有可搜索的数据与未加密的索引; 本文的工作是对不同数据所有权假设的一个补充;
• 本文假设一个查询包含至少两个单词, 因为处理单个单词查询相对容易, 只需要在服务器上存储加密的对每个单词的预排序文档编号即可;
  • 备注: 单个单词查询直接用倒排索引就可以很容易的解决, 找到那个单词, 然后排序索引值;

5. 本文的贡献:

• 本文提供一个索引的, 线上的搜索schema, 使用一个线性累积函数对于这个开放的私有topK搜索问题;
• 本文通过部分的服务端结果过滤来寻求平衡, 以处理一个中等大小的数据集;
• 本文的速度比之前的baseline方案(文献13)要快上几个量级, 并且容纳了四种预先建立的排序信号(previously-developed ranking signals);
• 由于篇幅所限, 本文只列出正式的性质而忽略详细证明;

---

第二节 问题定义与设计考虑 PROBLEM DEFINITION AND DESIGN CONSIDERATIONS

1. 问题定义:

• 给定$D$个文档特征向量, 客户端拥有$T$个特征(可以理解为词汇表大小), 每个文档$d$有许多特征值, 用$f_i^d$表示;
• 客户端建立一个可搜索的索引然后将它传递给服务器;
• 我们着重于建立一个索引和topK搜索schema使得服务器可以获得一次查询的加密匹配文档特征, 然后在合理的响应时间内在中等大小的数据集上计算他们的排序而无需知道底层特征值;
• 服务器同样不应该学习到任何有意义的信息当搜索中没有涉及到特征;
• 本文假设每次搜索查询包含一个联合的关键词组, 并采用基于可搜索加密算法OXT(参考文献16与17)的查询单词的倒排索引项合并(posting intersection);
• 更快的传统合并(intersection)算法, 如同时遍历两个或更多的倒排索引项(postings)的算法, 没有被采用的原因是这样一个遍历机制会给服务器泄露更多的信息;
• 在搜索过程中, 一个用于确保隐私的标准技术是使用确定性的伪随机函数(PRF)来隐藏包括项目编号与文档编号在内的信息;

2. 排序公式:

• 本文期望得到一个简单但流行的排序评分计算schema, 这种算法应当是文档特征的线性组合;
• 虽然文献47的评分传达不错的相关性表现, 多个累积树(multiple additive tree, 文献44提到)可以取得更好的相关性;
• 尽管如此, 将这样一个非线性的排序方法转为私有, 不仅涉及得分增加, 也会涉及值比较; 目前仍然没有可用的加密方法能够在一个单一框架中解决这两个问题;
• 本文提出一个线性组合公式来计算排序得分: ${\sum }_i{\alpha }_i{f}_i^d$
  • 其中${\alpha }_i$是关于文档$d$的特征值$f_i^d$的系数;
  • 假设所有的系数都是静态的, 并且可以在索引安装(setup)时嵌入到特征值中;
  • 本文的剩下部分将忽略这些系数, 即线性累积排序公式简化为: ${\sum }_i{f}_i^d$

3. 原始排序特征:

• 定义: 称一个排序特征是原始的(raw), 若它是直接存储在索引中; 称一个排序特征是合成的(composite), 若它是基于其他原始特征计算得到的;
• 本文的设计是使得第2点的排序公式中的每个基础特征(basic feature)都作为原始特征, 服务器检索到之后直接简单地将他们加进来, 而无需知道这些值所扮演的角色; 这就最小化了服务器理解他们对于排序信号(ranking signal)做出的语义贡献(semantic contributions)的可能性了;
  • 备注: 所谓语义贡献我理解可以视为语义安全中的攻击者优势, 语义安全相关见[affliation.md]
• 我们使用第2点的排序公式来支撑4种用于信息检索文献(information retrieval literature)的排序特征:
  • ① 基于项频(term-frequency)的合成特征: 如TF-IDF与BM25;
    • 备注: TF-IDF上面已经提过, 本质上就是用IDF作为权重来加全TF(词频), 而BM25是计算词条与文档相似度的算法, 主要基于以下三个值:
      • ① 单词和D之间的相关性
      • ② 单词和query之间的相关性
      • ③ 每个单词的权重
      • $Score(Q,d)={\sum }_i^n{W}_{i}R(q_i,d)$, 其中$W_i$就是TF-IDF中的idf值作为权重, $R(q_i,d)=f_i$