FedFomo论文阅读笔记

Posted 2022-12-06 联邦学习小白

《PERSONALIZED FEDERATED LEARNING WITH FIRST ORDER MODEL OPTIMIZATION》是ICRL-2021的一篇个性化联邦学习文章。该文章通过赋予客户一个新的角色，并提出一种新的权重策略，构造了一种在隐私和性能之间进行权衡的新的联邦学习框架。

创新点：

• 传统的联邦学习目标是训练一个全局模型，个性化联邦学习则认为单一的全局模型难以收敛，且并非在每个客户上都有很好的表现。
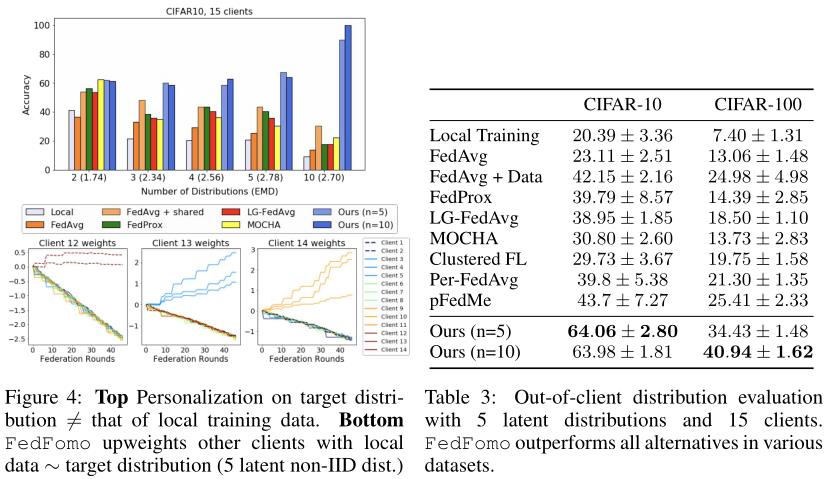
  这篇文章也是基于个性化的想法，同时赋予客户一个新的角色。提出服务端保存每个客户的模型，让客户从服务端下载在本地目标任务具有良好性能的模型。这样，即便本地目标任务的数据分布不同于训练数据分布，该客户也可以训练出能实现本地目标任务的模型。
• 文章还提出一种新的权重策略来对从服务端下载的模型进行加权聚合并对本地模型进行更新。
• 到这里大家应该会想到一个问题，没错就是隐私问题。之所以要有个服务端，其中一方面的原因就是为了防止客户之间的直接接触，而文章提出的这种方法客户会直接获得其他客户的模型。对于这个问题，文章也提出了利用差分隐私来进行加密处理，在隐私和性能之间进行权衡。

文章提出的框架——FedFomo

传统的联邦学习框架如FedAvg是让被选中的客户上传其模型参数，并在服务端对这些模型参数以所在客户端地相对数据量为权重进行平均聚合，得到一个单一的全局模型，各客户下载该全局模型进行本地训练，以此循环进行上传——聚合——下载。FedFomo也类似这种模式，只不过对上传、聚合、下载的方式大有不同。

• 上传：每个客户基于本地数据进行训练，并将训练后的模型参数上传至服务端，服务端保存每个客户在本地任务 l 和此轮通信 t 的模型${\theta }_n^{l(t)}$。
• 下载：不同于传统的联邦学习中每个客户端下载一个全局模型，这里需要分两步：

1. 服务端计算要将哪些模型发送给哪些客户。
2. 客户端收到这些模型后，通过这些模型${\theta }_n^{l(t)}$以及自己在上一轮的模型${\theta }_i^{l(t-1)}$在本地验证集（验证集与测试集具有相似的数据分布）上的Loss来计算这些来自其他客户的模型的聚合权重$w_n$，即
   ${\theta }_i^{l(t)}$ ⬅ ${\theta }_i^{l(t-1)}$ + ${\Sigma }_{n\in [N]}{w}_n({\theta }_n^{l(t)}-{\theta }_i^{l(t-1)})$
   首先我们看$w_n$，若客户收到的模型在本地验证集的Loss比本地模型小，那就说明这个模型有利于这个客户的目标任务，也就是权重$w_n$ > 0，而该模型性能越好，$w_n$便越大，权重越高。
   
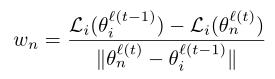
   而若$w_n$ < 0，说明该模型并不比本地模型好，此时$w_n$不取负数，而是直接令为0，即$w_n$ = max($w_n$, 0)。
   需要注意的是，所有值大于零权重还需进行标准化处理，即其他客户端模型的最终权重$w_n^{\ast }$ = max($w_n$, 0) / ${\Sigma }_n$ max($w_n$, 0)。
   到这里都是在说其他客户端模型的权重怎么算，那本地模型的权重呢？本地模型的权重直接通过$L_i({\theta }_i^{l(t-1)})$ - $L_i({\theta }_i^{l(t)})$来计算，这么定义可以防止过拟合，也就是当$L_i({\theta }_i^{l(t-1)})$ - $L_i({\theta }_i^{l(t)})$ < 0时将触发
   “early-stopping”。

现在我们回到下载中的第一步，也就是要将哪些模型发送给哪些客户的问题，其实理想情况下，我们应该是让每个客户下载所有模型，按照第二步中定义的权重策略分别计算每个模型的权重，然后挑选权重最高的若干个进行聚合，进而对本地模型进行更新。然而实际应用中我们要考虑带宽、计算、时间代价等问题，不可能去这么做。
因此，文章给出了一个解决方案。首先，定义全体客户数量为K，活跃客户（能参与训练）数量为N，限制每个客户能下载的最大模型数量为M，以此为基础，文章进一步提出通过前一轮通信中，模型${\theta }_j$在客户$c_i$的目标任务上的性能决定是否将${\theta }_j$分给$c_i$。具体来讲分为两种情况：

1. 作者定义了一个由向量$p_i$ = < $p_{i,1}$ ,…, $p_{i,k}$ >组成的关联矩阵P，其中$p_{i,j}$为将${\theta }_j$发送给客户$c_i$的概率。一开始P = diag(1,…,1)，ie.每个模型被下载的机会平等。接下来在每轮通信中，p ⬅ p + w，w也就是第二步中定义的权重，并且这里w可以为负数。
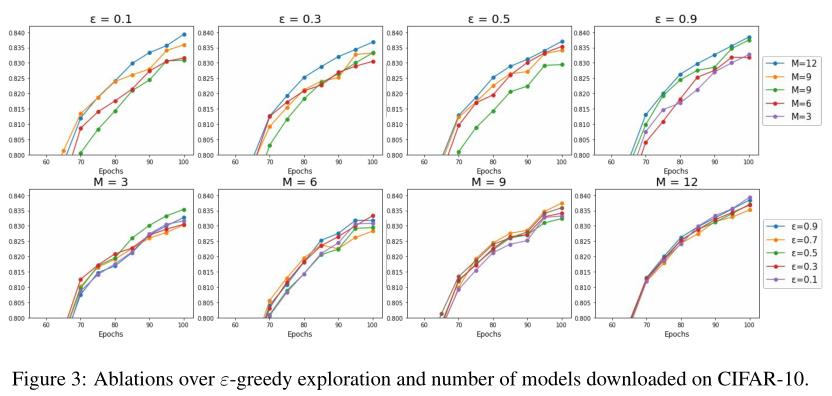
2. 前面我们一直在考虑模型太多，怎么选择的问题，那可用模型太少呢？这就是第二种情况了，也就是活跃客户太少的情况：N << K。对于这种情况，文章提出采样ε-greedy采样策略，该策略并非按概率p进行采样，而是有ε的概率将一个随机模型发送给客户端。

所以总的来说，文章通过参数ε和M来决定模型的分配问题。

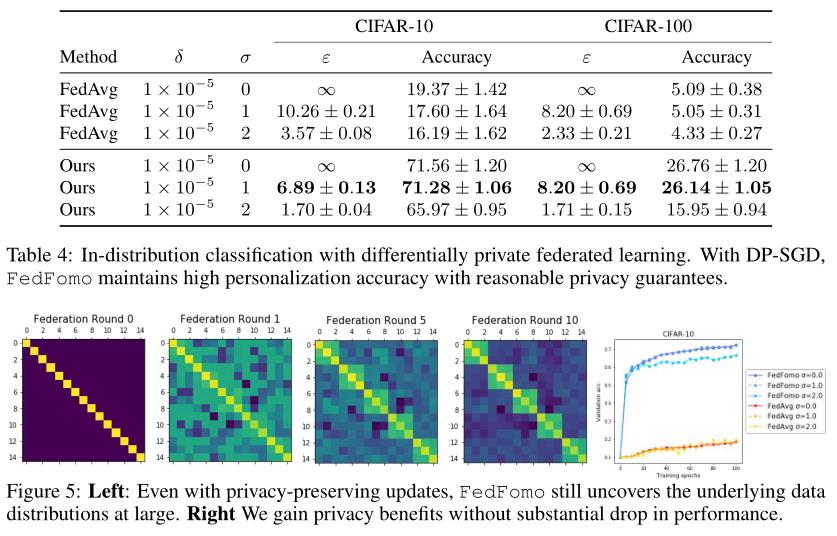
• 隐私保护问题：正如前面提到的，让客户直接下载其他客户的模型会导致隐私泄露问题，针对这一点，文章提出在(ε, δ)-differential privacy（DP）下进行FedFomo的训练，简单地说，DP可以实现当你查看两个不同的数据集时，观察到的结果是一样的。 将DP应用于FedFomo主要是看中其可组合性和对后续处理的鲁棒性，它确保了当我们训练的模型参数θ满足DP时，θ上的任何函数也是DP。然后使用DP- SGD在本地对FedFomo的DP变体进行训练，该变体为每个梯度添加了可调数量的高斯噪声，并在本地训练数据中减少了模型更新和个体样本之间的联系。更多的噪音会以性能为代价提高模型的加密程度。文章对FedFomo在嘈杂的本地更新下是否能在提高加密程度的情况下保持性能做了具体实验。

实验

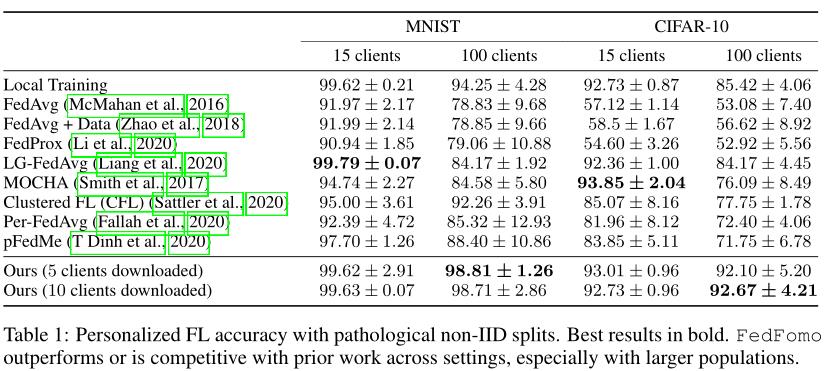
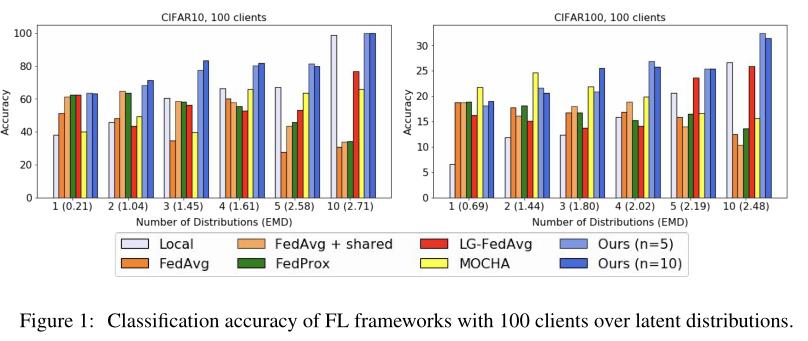
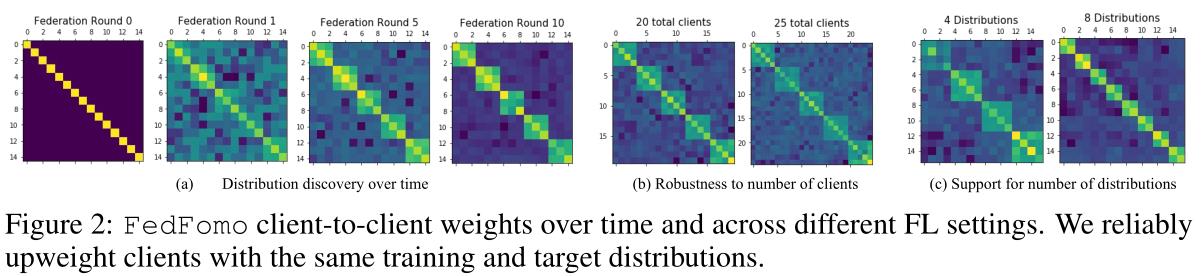
隐私和性能的权衡