机器学习基础

Posted 2022-04-20 彭祥.

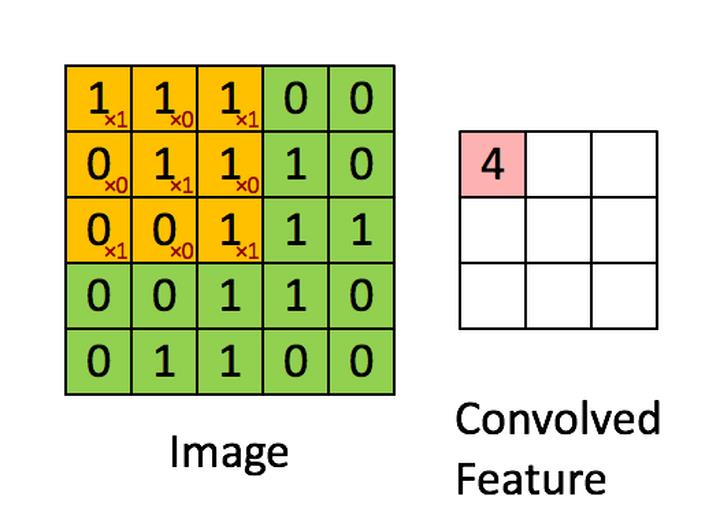
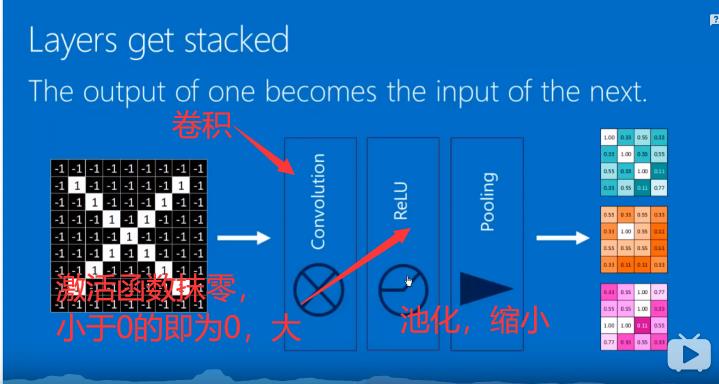
在卷积神经网络中，所谓的卷积运算，其实并不是严格的数学意义上的卷积。深度学习中的卷积实际上是信号处理和图像处理中的互相关运算，它们二者之间有细微的差别。深度学习中的卷积（严格来说是互相关）是卷积核在原始图像上遍历，对应元素相乘再求和，得到的新图像在尺寸上会有减小。可以通过下图直观的去理解。假设输入图像的有m行,n列，卷积核的尺寸为filter_size×filter_size，输出图像的尺寸即为**(m-filter_size+1)×(n-filter_size+1)**

在全连接神经网络，图像数据以及特征是以列向量的形式进行存储。而在卷积神经网络中，数据的格式主要是以张量（可以理解为多维数组）的形式存储。图片的格式为一个三维张量，行×列×通道数。卷积核的格式为一个四维张量，卷积核数×行×列×通道数。

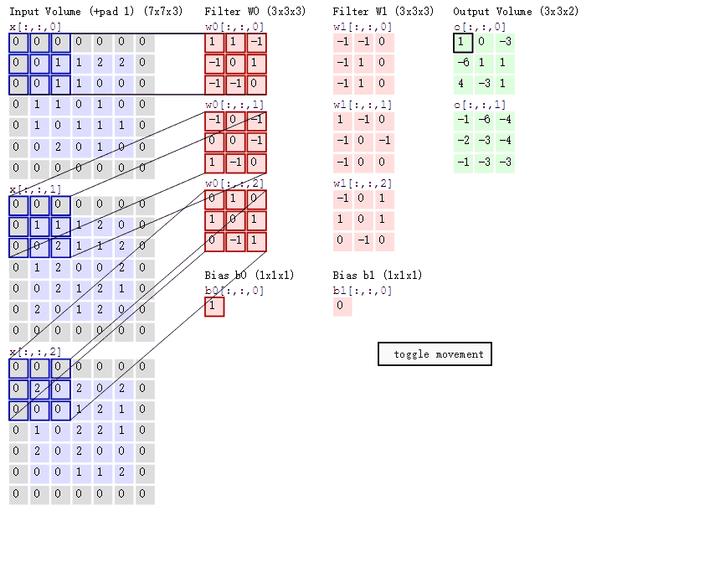
卷积操作是每次取出卷积核中的一个，一个卷积核的格式为三维，为行×列×通道数。对应通道序号的图片与卷积核经过二维卷积操作后（即上图所示操作），得到该通道对应的卷积结果，将所有通道的结果相加，得到输出图像的一个通道。每个卷积核对应输出图像的一个通道，即输出图像的通道数等于卷积核的个数。

这里概念有一点绕，但是卷积神经网络中所谓张量的卷积，本质上是进行了一共卷积核数×通道数次二维卷积操作。每一个卷积核对应卷积结果的一个通道，每一个卷积核的通道对应原始图片的一个通道。这个操作和一个列向量乘上一个矩阵得到一个新的列向量有相似的地方。
卷积核，也就是我们说的过滤器
下图直观地展示了张量卷积具体操作过程：

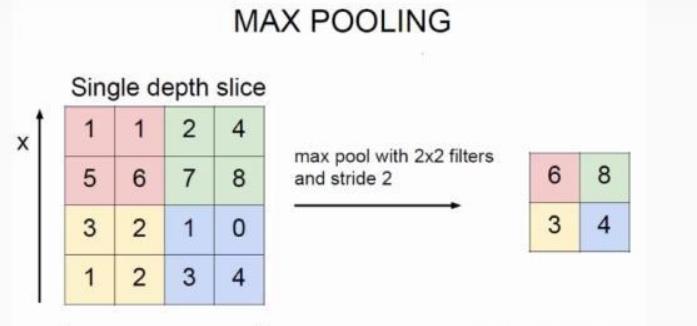
所谓的池化，就是对图片进行降采样，最大池化就是在图片中用每个区域的最大值代表这个区域，平均池化就是用每个区域平均值代表这个区域。

池化层反向传播
池化层的反向传播比较容易理解，我们以最大池化举例，上图中，池化后的数字6对应于池化前的红色区域，实际上只有红色区域中最大值数字6对池化后的结果有影响，权重为1，而其它的数字对池化后的结果影响都为0。假设池化后数字6的位置delta误差为x，误差反向传播回去时，红色区域中最大值对应的位置delta误差即等于 x ，而其它3个位置对应的delta误差为0。

因此，在卷积神经网络最大池化前向传播时，不仅要记录区域的最大值，同时也要记录下来区域最大值的位置，方便delta误差的反向传播。

而平均池化就更简单了，由于平均池化时，区域中每个值对池化后结果贡献的权重都为区域大小的倒数，所以delta误差反向传播回来时，在区域每个位置的delta误差都为池化后delta误差除以区域的大小。

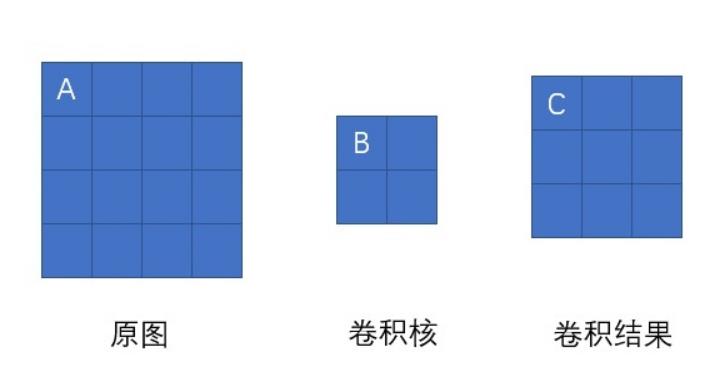
如上图所示，我们求原图A处的delta误差，就先分析，它在前向传播中影响了下一层的哪些结点。显然，它只对结点C有一个权重为B的影响，对卷积结果中的其它结点没有任何影响。因此A的delta误差应该等于C点的delta误差乘上权重B。

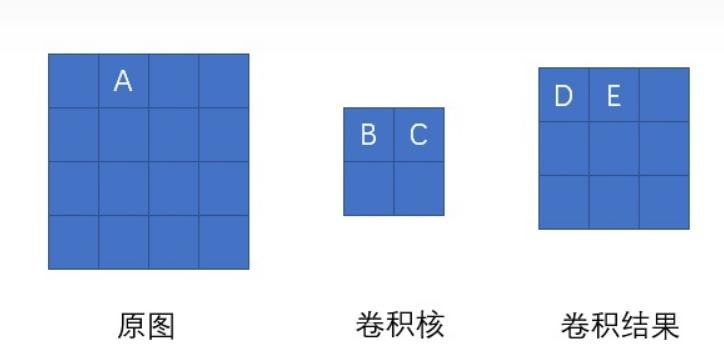
我们现在将原图A点位置移动一下，再看看变换位置后A点的delta误差是多少，同样先分析它前向传播影响了卷积结果的哪些结点。经过分析，A点以权重C影响了卷积结果的D点，以权重B影响了卷积结果的E点。那它的delta误差就等于D点delta误差乘上C加上E点的delta误差乘上B。

参考：添加链接描述

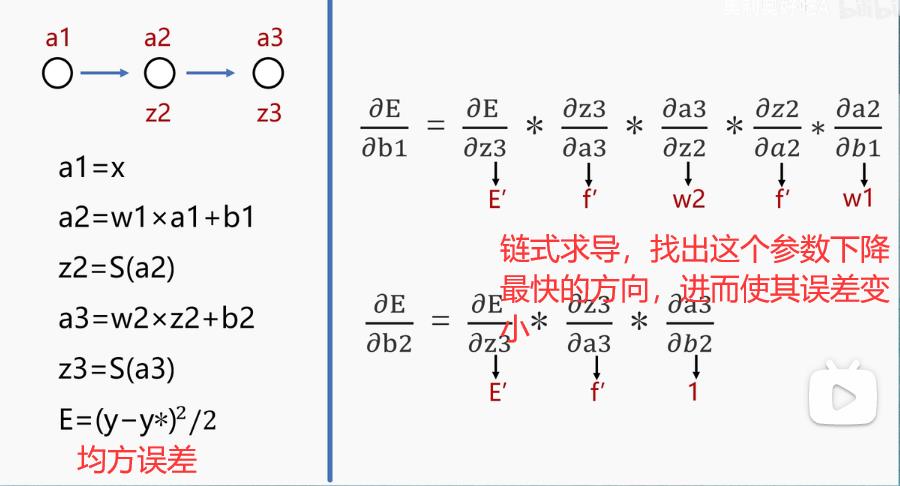
关于BP神经网络的反向误差传播算法的理解


而误差反向传播则是通过输出值的差值来计算误差，从而让误差沿着w,b方向减少


输入层的参数个数取决于特征数目，输出层取决于分类类别，中间层我们可以凭借经验
此外还要注意学习率的设定

学习率的重要性
1）学习率设置太小，需要花费过多的时间来收敛
2）学习率设置较大，在最小值附近震荡却无法收敛到最小值
3）进入局部极值点就收敛，没有真正找到的最优解，局部最小值
4）停在鞍点处，不能够在另一维度继续下降
梯度下降算法有两个重要的控制因子：一个是步长，由学习率控制；一个是方向，由梯度指定。

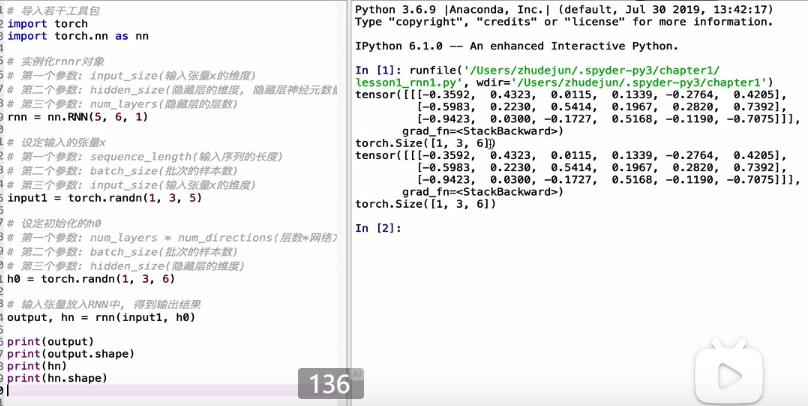
实现RNN案例

梯度爆炸与梯度消失

RNN的优缺点

LSTM介绍

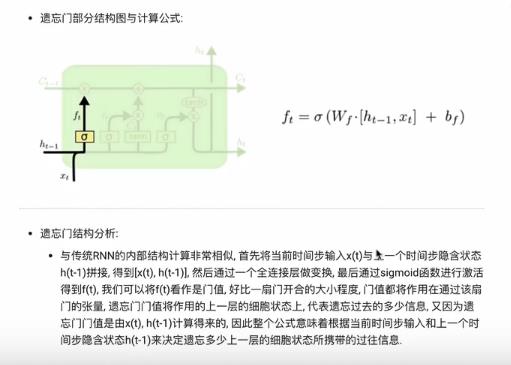
遗忘门

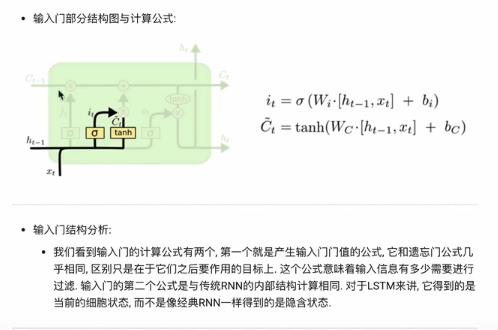
输入门

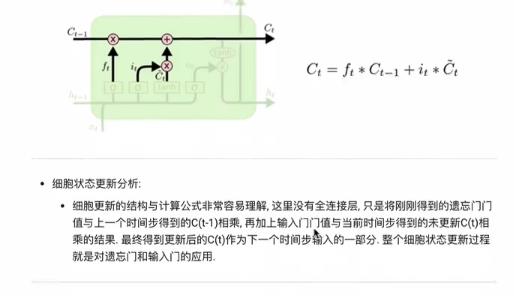
细胞状态更新

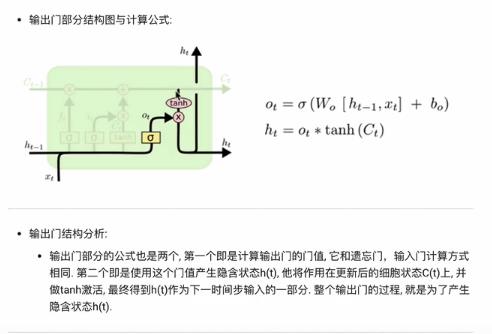
输出门

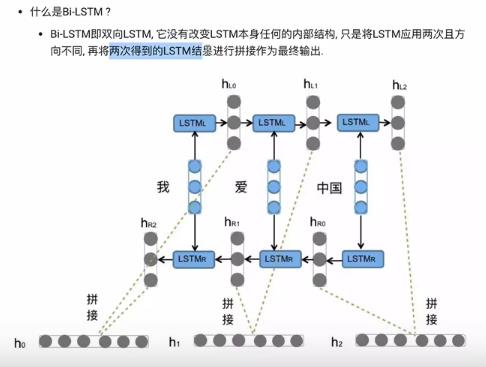
Bi LSTM

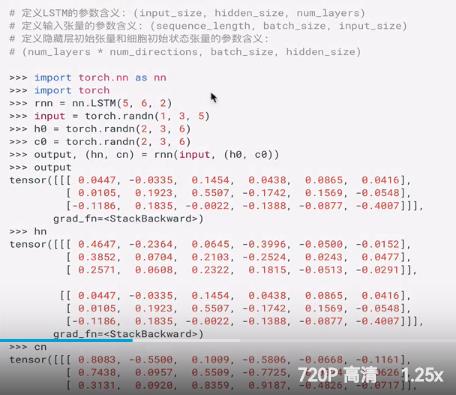
案例实现

LSTM 文章