机器学习--基础知识复习(模式识别,成本函数)
Posted dinghing
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习--基础知识复习(模式识别,成本函数)相关的知识,希望对你有一定的参考价值。
由于时间原因,今天主要复习下machine learning课程的前三节,简单记录自己的理解。
1.模式表达(Model representation)
其实就是指通过一定的范例数据学习追踪生成一个函数的表达形式。然后通过矩阵得到整个运算过程。
模型表达就是给出输入和输出之间的函数关系式,当然这个函数是有前提假设的,里面可以含有参数。
比如下图,我们有一个房子的大小size,卧室数目(bedrooms)然后得到房屋价格(price),通过这三个常数就可计算一个输入和输出的函数关系。
hprice=Q0+Q1*size+Q2*bedrooms;
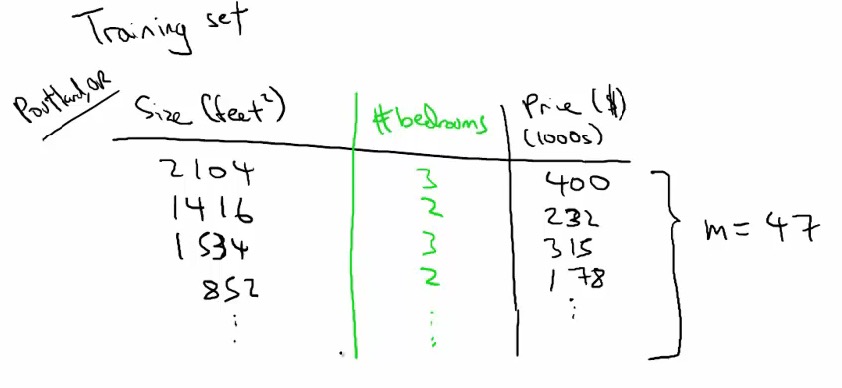
在求解过程中透露出了两个信息:
1.房价模型是根据拟合的函数类型决定的。如果是直线,那么拟合出的就是直线方程。如果是其他类型的线,例如抛物线,那么拟合出的就是抛物线方程。
机器学习有众多算法,一些强力算法可以拟合出复杂的非线性模型,用来反映一些不是直线所能表达的情况。
2.如果我的数据越多,我的模型就越能够考虑到越多的情况,能够由损失函数越小,由此对于新情况的预测效果可能就越好。
一般来说(不是绝对),数据越多,最后机器学习生成的模型预测的效果越好。
2.成本函数(cost funtion)
此时如果有许多训练样本的话,同样可以给出训练样本的平均相关的误差函数,
一般该函数也称作是成本函数(cost function)。我们的目标是求出模型表达中的参数,这是通过最小化成本函数来求得的。
通常来说,模型越准确,越接近真实,其cost function的值就越小
在线性回归问题中,通常使用square loss的形式。线性回归常用的square loss形式是均方误差MSE:
Jθ=1m(hθ(x(i))−y(i))2

一般最小化成本函数是通过梯度下降法(即先随机给出参数的一组值,然后更新参数,使每次更新后的结构都能够让损失函数变小,最终达到最小即可)
通常上面的方差运算也有以下表达方式:
Jθ=12m(hθ(x(i))−y(i))2
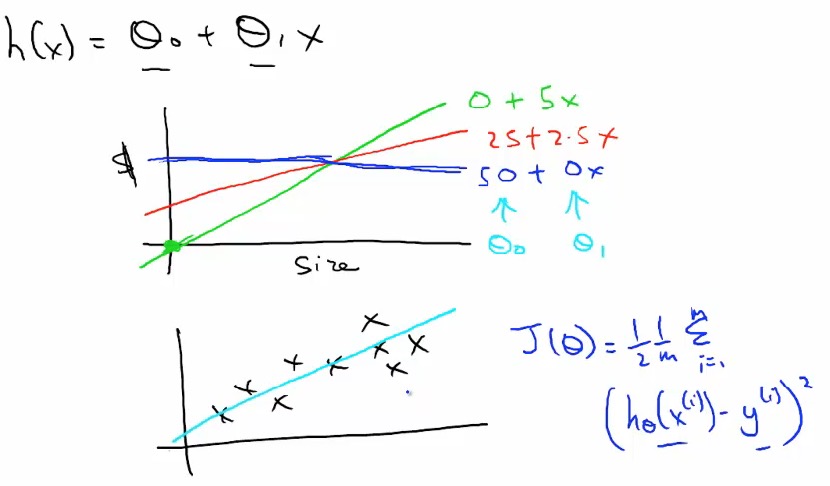
对于上图当我们画图表示的时候我突然联想到了入门时的那张图
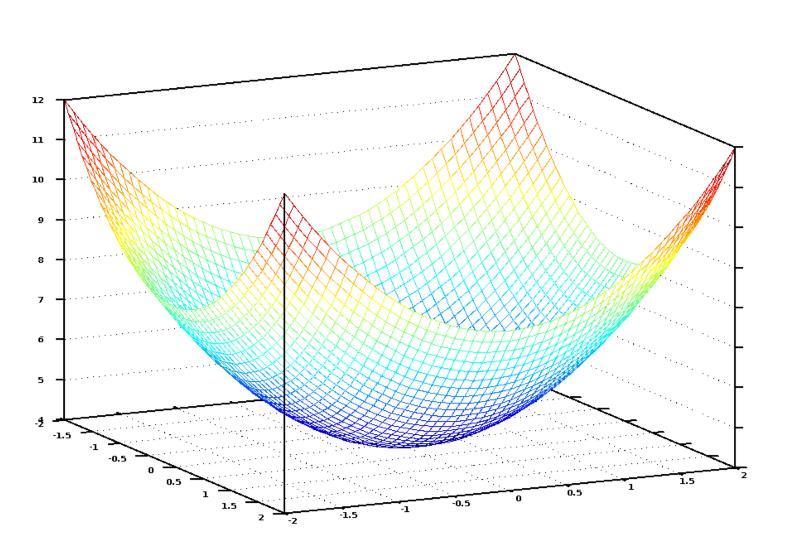
其全局极值点的坐标,就是我们要求的权重向量θ。
阶段总结:到目前为止,以我的理解,一个问题抽象成机器学习常用的过程就如下:
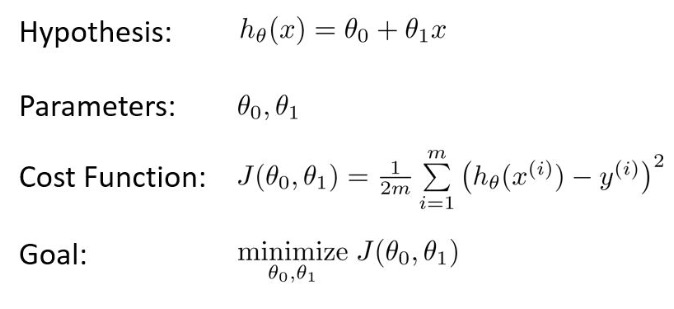
确定hypothesis,cost function和goal,通常对cost function 求解权重向量的过程,是一个最优化问题。
以上是关于机器学习--基础知识复习(模式识别,成本函数)的主要内容,如果未能解决你的问题,请参考以下文章
模式识别与机器学习——PART2 机器学习——统计学习基础——Regularized Linear Regression