模式识别与机器学习（更新中）

Posted 2023-02-03 中二病没有蛀牙

模式识别与机器学习

使用的教材，PPT为¹

公式推导部分直接去看白板推导²，不管是书上还是ppt都写的极其模糊

先说重点：

• 贝叶斯算概率
• 参数估计

第二讲 贝叶斯学习基础

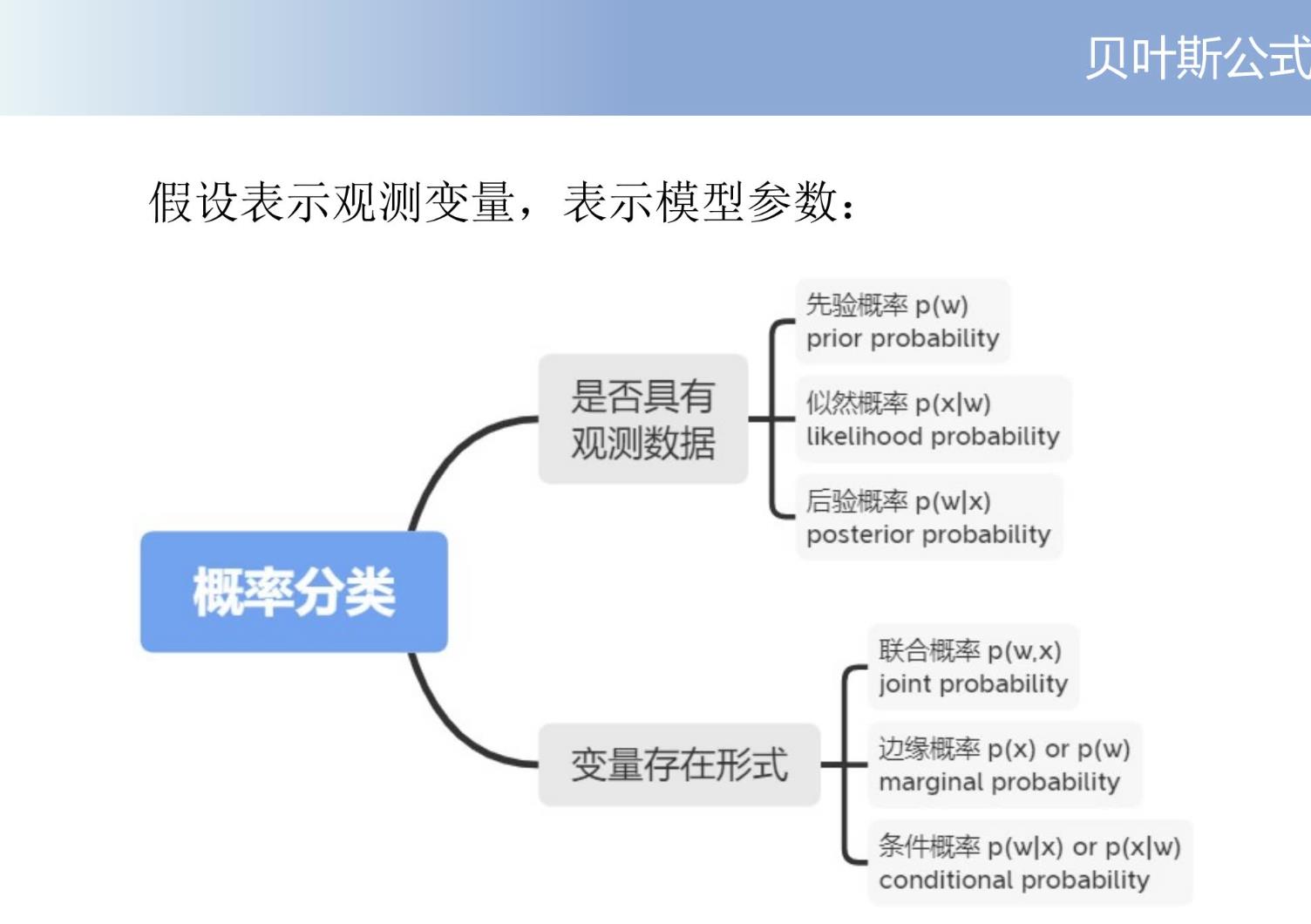
贝叶斯公式

先验概率是非条件概率

似然概率是给定变量的条件下观测变量的概率

后验概率是给定数据的条件下观测变量的概率

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7GOhpfgD-1668623635075)(PRML.assets/image-20221113232749527.png)]

贝叶斯决策

最小错误率贝叶斯决策

决策的平均错误率尽可能地小。

二分类

也就是说后验概率大的就是所求的。

多分类

对于更一般化的多类分类问题，最小错误率决策表示为最大化平均正确率

可能错分的情况存在种，涉及到的计算很多，所以通常采样计算平均正确率来计算

• 所有的类别分母都是相同的，所以决策时实际上只需比较分子即可。

最小风险贝叶斯决策

最小化决策带来的平均损失，也叫做最小化风险（risk）

平均损失的两重含义

• 获得观测值后，决策造成的损失对实际所属类别的各类可能的平均，称为条件风险（conditional risk）
• 条件风险对x的数学期望，称为总体风险
• 

最小错误率是最小风险的一种特殊情况

关于两种方式的区别去看书上p38 题二

分类器

分类器是一个计算系统，它通过计算出一系列判别函数的值做出分类决策，实现对输入数据进行分类的目的。分类器的构建离不开判别函数和决策面。

判别函数是一个从输入特征映射到决策的函数，其结果可以直接用于做出分类决策。

分类问题中，分类器会把输入空间划分成多个决策区域，这些决策区域之间的边界称作决策面或决策边界。

分类器的构建方法

• 生成模型：基于概率框架和贝叶斯决策，如朴素贝叶斯模型
• 判别式模型：基于概率框架,输出类别在输入特征下的条件分布，如逻辑回归，SVM
• 直接构建：不用概率表示，直接输出结果

区别[^10]：

生成式模型举例：利用生成模型是根据山羊的特征首先学习出一个山羊的模型，然后根据绵羊的特征学习出一个绵羊的模型，然后从这只羊中提取特征，放到山羊模型中看概率是多少，在放到绵羊模型中看概率是多少，哪个大就是哪个。

判别式模型举例：要确定一个羊是山羊还是绵羊，用判别模型的方法是从历史数据中学习到模型，然后通过提取这只羊的特征来预测出这只羊是山羊的概率，是绵羊的概率。

基于高斯分布的贝叶斯分类器

协方差（Covariance）在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。

协方差矩阵可以参考这篇[3]：https://eipi10.cn/mathematics/2021/05/12/covariance_matrix/

不同维度下的判别面：

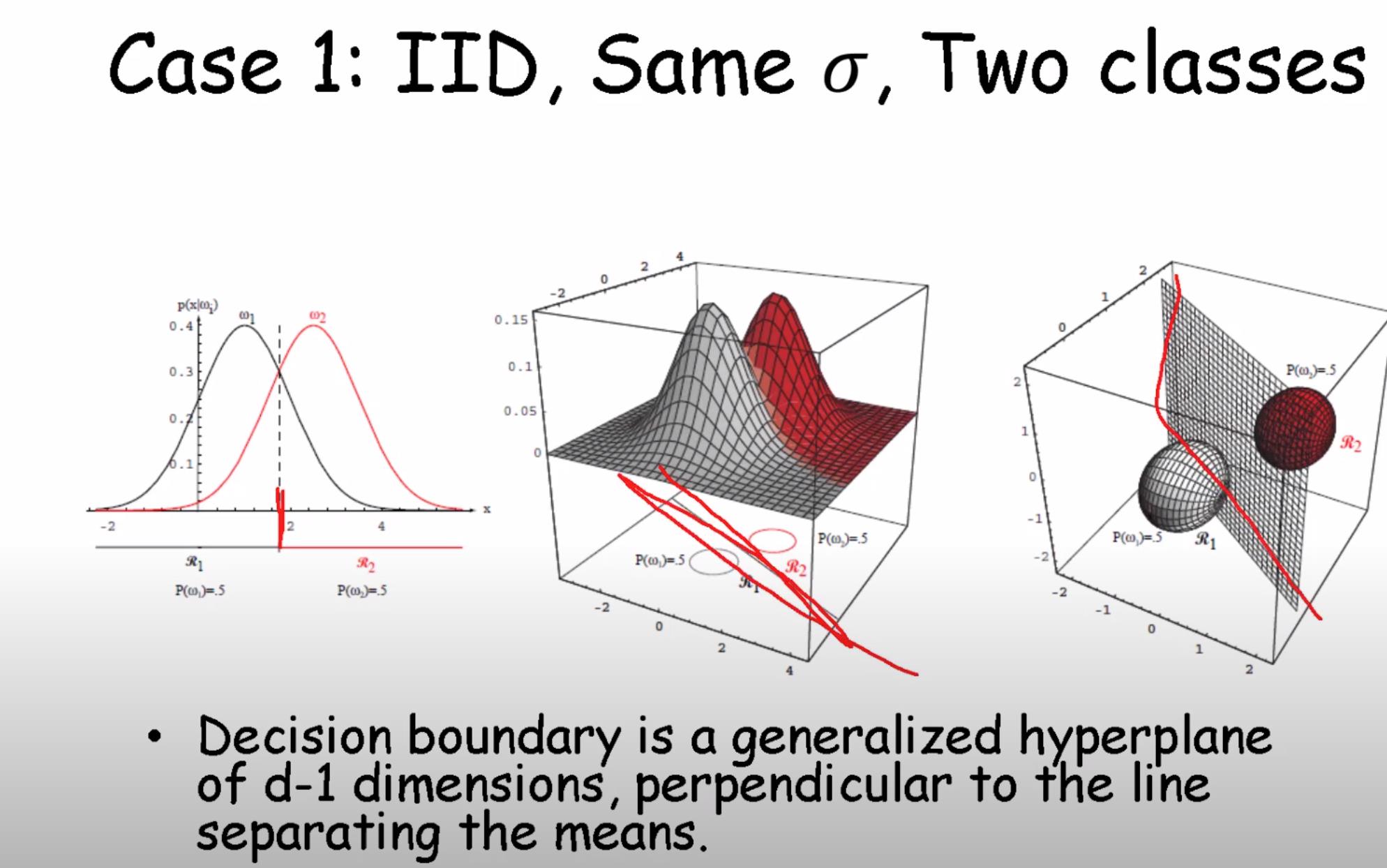
朴素贝叶斯分类器

朴素贝叶斯（naïve Bayes）分类器对条件概率分布提出了特征条件独立的假设，所谓的朴素就是特征条件独立

朴素贝叶斯假设向量的D个元素之间相互独立，其联合分布可以写成 D个独立的概率分布相乘。也就是所有特征的联合分布。

参数估计

最大似然估计

极大似然估计中采样需满足一个重要的假设，就是所有的采样都是独立同分布的。

最大似然估计是一种给定观测时估计模型参数的方法，它试图在给定观测的条件下，找到最大化似然函数的参数值。

就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值

最大后验估计

最大后验估计是在最大似然估计的基础上考虑参数的先验分布，通过贝叶斯公式获得参数的后验分布 ，并以后验分布作为估计的优化目标。参数θ的最大后验估计KaTeX parse error: Expected 'EOF', got '̂' at position 3: θ ̲̂_map表示为

期望最大化算法（expectation maximization，EM）

栗子：调查吸毒比例，隐藏问卷中的哪个问题。

本质：既然无法求解隐变量，就不求了，直接假设一个初始值代入计算，有了结果之后再进行迭代。³

例：对不完整数据建模时，使用隐变量定义缺失数据；

对复杂的观测数据建模时，使用隐变量定义潜在因素。

考虑一个概率模型，X表示观测变量集，Z表示隐变量集，θ表示模型参数，目标是最大化观测变量X对参数θ的对数似然函数：

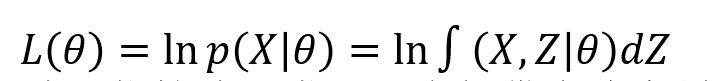
EM算法是一种迭代算法，常用于求解带有隐变量的概率模型的最大似然或者最大后验估计。

E步：根据给定观测变量X和当前参数θ推理隐变量Z的后验概率分布，并计算观测数据X和隐变量Z的对数联合概率关于Z的后验概率分布的期望；

（人话：已知X,$\theta$估计缺失的Z的估计值， 这也是为啥是Z的后验概率，因为给了X；

但是Z是隐含起来的，所以这个期望只能对整体的联合求，当然优化的目标也是整体的联合概率，只不过里头隐含了Z）

M步：最大化E步求得的期望，获得新的参数θ。

贝叶斯参数估计

认为参数同样是一个随机变量，服从一个先验分布，可以计算给定数据后的后验分布.

贝叶斯参数估计得到的是参数θ在给定观测数据集D的后验分布

第三讲 逻辑回归

线性回归

基函数（basis function）：对输入特征的变换函数

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-znPVxhpV-1668623635261)(http://picbed.elcarimqaq.top/img/image-20221113003252464.png)]

• 多项式基函数的一个局限性是它们是输入变量的全局函数，所以一个区域内个改变会影响所有区域。

• ${\mu }_j$控制着基函数在输入空间中的位置，参数$s$控制着基函数的空间大小

• 可以对自变量进行非线性变换，在得到新的自变量后进行线性回归建模。

使用高斯随机噪声实现概率建模

概率线性回归的一种方式是高斯随机误差概率建模，观测的输出被假设为确定性的线性回归加上一个高斯随机噪声

最小二乘与最大似然

最小二乘问题的目标为调整模型函数的参数来最好地拟合数据集。模型对数据的拟合程度是通过其误差来测量的。

最大似然是因为减去的是似然，要越大越好

二乘的意思就是误差乘两次

最小值可通过将对优化目标关于参数的导数设为0求解得到。

模型有D个参数，就有D个梯度方程

P9

P10

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-icnUFpye-1668623635270)(http://picbed.elcarimqaq.top/img/image-20221114001129822.png)]

正则化最小二乘与最大后验

使用L_2范数作为惩罚项的正则化最小二乘也叫做岭回归。

Lasso回归

P11

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WOAfHi9Y-1668623635271)(http://picbed.elcarimqaq.top/img/image-20221114001310286.png)]

逻辑回归

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BvskOez9-1668623635275)(PRML.assets/image-20221113203119577.png)]

第四讲 概率图模型基础

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9iGcjyiA-1668623635280)(PRML.assets/image-20221113203908290.png)]

有向图

概率图的构建可以由拓扑排序

一个贝叶斯网络由两部分组成：

①有向无环图G=(V,E) ，其中V表示有向图中节点的集合，E表示图中有向边的集合。

②父节点到子节点的条件概率分布。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zjPntGMF-1668623635293)(PRML.assets/image-20221113233956430.png)]

局部马尔可夫性：贝叶斯网络中每一个节点在给定其父节点的条件下与其他非后代节点条件独立。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DKvVJMWe-1668623635306)(PRML.assets/image-20221113210901950.png)]

顺序结构（head to tail)

节点𝑐连接了一个箭头的头部和另一个箭头的尾部。

顺序结构具有条件独立性：在给定𝑐的条件下，𝑎和𝑏条件独立。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Fjhbk8w3-1668623635324)(PRML.assets/image-20221113210623985.png)]

发散结构（tail to tail）

节点c连接两个箭头的尾部。

发散结构具有条件独立性：在给定c的条件下，a和b条件独立。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wFLJoPmN-1668623635326)(PRML.assets/image-20221113210659293.png)]

汇总结构（head to head）

节点c连接了两个箭头的头部。

汇总结构不具有条件独立性：在给定c的条 件下，a和b条件不独立。 只有这个是特殊的

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-O1PAk9CJ-1668623635336)(PRML.assets/image-20221113210725335.png)]

d-分隔规则

例子：

马尔可夫毯（Markov blanket）

参考[4] https://blog.csdn.net/jbb0523/article/details/78424522

说人话就是最后留下的是该点的父亲，儿子，儿子的其他父亲

常见的有向图模型

朴素贝叶斯和隐马尔可夫模型

朴素贝叶斯网络

**隐马尔可夫模型（**hidden Markov model）

无向图模型⁴

定义

一个无向图模型(Undirected Graphical Model)，又被称为马尔科夫随机场(MRF,markov random field)， 也可以被称为马尔科夫网络(Markov network)。

任一变量x_k在给定它的邻居的情况下条件独立于所有其他变量，表示为x_k在给定邻居变量和给定其他所有变量条件下的概率分布相同

条件独立性体现在：全局，局部，成对

无向图中的一个全连通子图，称为团（clique），即团内的所有节点之间都有边相连。

在所有团中，如果一个团不能被其它的团包含，这个团就称作一个最大团（maximal clique）。

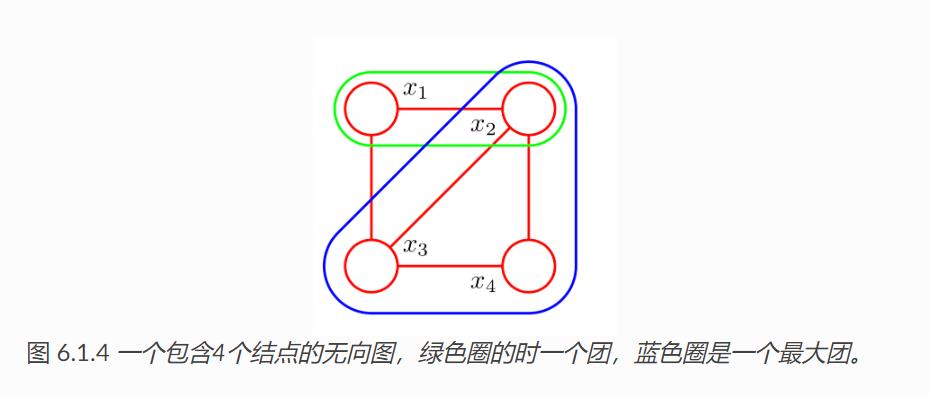
条件独立性

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qWpFS4pk-1668623635396)(http://picbed.elcarimqaq.top/img/image-20221114124203857.png)]

图分解

根据概率论中的链式法则，联合概率分布可以分解成”局部函数”的乘积形式

无向图表示的联合概率分布可以分解成定义在团上的局部函数的乘积， 我们将这个局部函数称为势函数(potential function)。

例子：无向图的联合概率分布

图模型中的推理

因子图⁵

将一个具有多变量的全局函数因子分解，得到几个局部函数的乘积，以此为基础得到的一个双向图叫做因子图（Factor Graph）。

因子图在变量节点（下图中圆形表示）外，额外引入了因子节点（下图中方形表示）

因子图与图模型的对应关系：

• 因子图中的变量节点与对应图模型中的变量节点相同；

• 因子图中对应图模型中同一因子的变量节点之间存在一个因子节点；

• 因子图中的边都是无向边，连接因子节点与相对应的变量节点。

因子图主要有两个用途，1）表达因子分解的结构，2）计算边缘函数。

因子分解⁶

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8HqR6HIa-1668623635402)(PRML.assets/image-20221114152422112.png)]

$p(X)$分解为几个局部函数的乘积，每个函数的参数均为 X 的子集

边缘函数

$X−xi $为 $X$ 中除$ xi $之外的其他元素组成的集合，则称$pi(xi)$为$ p(x1,x2,…,xn)$ 的一个边缘函数 。

边缘函数的解就是边缘概率（先验概率）：某个事件发生的概率

边缘概率是通过边缘化（marginalization）得到的：在联合概率中，把最终结果中不需要的那些事件合并成其事件的全概率而消失（对离散随机变量用求和得全概率，对连续随机变量用积分得全概率）

和积算法

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-H9r10njQ-1668623635405)(PRML.assets/image-20221114160817793.png)]

和：求解的因子结节和它相连的变量节点的和

积：求解的因子节点和其他因子节点的积

和积算法的步骤如下：

① 选择任何一个变量节点或因子节点作为根节点；

② 由叶子节点向根节点执行一次消息传递；

③ 由根节点向叶子节点执行一次消息传递；

④ 根据边缘分布的计算公式得出任意变量节点的边缘分布。

参考⁵给出了直观的例子

求解边缘分布的例子可以见书上P95 第四题

支持向量机

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ogLbwbNE-1668623635411)(http://picbed.elcarimqaq.top/img/image-20221114233349815.png)]

支持向量机由简至繁有⁷:

• 线性可分SVM
  • 通过硬间隔最大化可以学习得到一个线性分类器，
• 线性SVM
  • 当训练数据不能线性可分但是可以近似线性可分时，通过软间隔(soft margin)最大化也可以学习到一个线性分类器
  • 软间隔：有一定的容错率，引入了松弛变量
• 非线性SVM
  • 当训练数据线性不可分时，通过使用核技巧(kernel trick)和软间隔最大化，可以学习到一个非线性SVM。

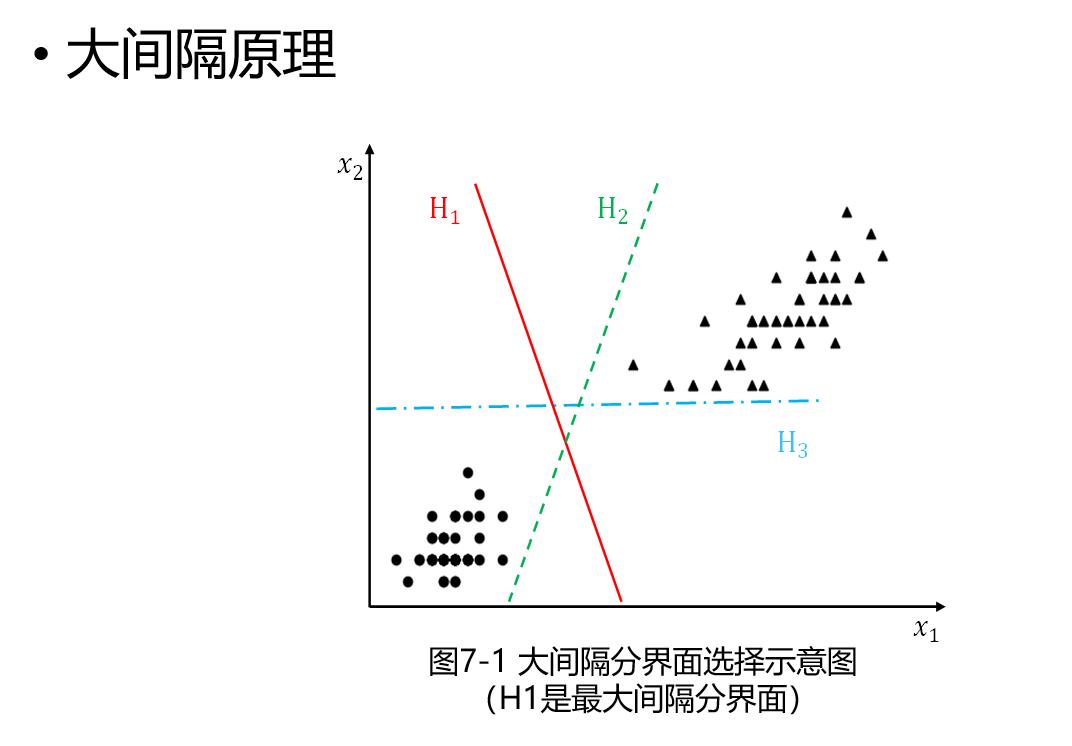
对于p维向量，用$p-1$维的超平面隔开所有点，SVM选择能够使每一类离超平面最近的数据点的距离最大的超平面。

样本中距离超平面最近的一些点，这些点叫做支持向量。

基本分类模型

间隔最大化问题的数学表达就是

具体的推导过程可以参考⁸

拉格朗日对偶优化

通过拉格朗日函数将约束条件融入到目标函数中，得到优化问题对应的拉格朗日函数为

线性不可分数据的分类

引入了软间隔

往年题

往年汇总

2021 ： https://blog.csdn.net/qq_40394960/article/details/112580581?spm=1001.2014.3001.5502

考点频率

EM算法

马尔科夫毯

2021

EM求解高斯混合

d-分割规则

FTTFF

2014

和积算法的过程是什么？

• 因子图，和积算法

马尔科夫毯的主要变量有哪些。

在可信贝叶斯网络中，一个节点的马尔可夫毯为该节点的父节点、子节点以及子节点的父节点。

参考资料

---

1. 《模式识别与机器学习》 ↩︎

2. https://www.bilibili.com/video/BV1aE411o7qd?p=3&vd_source=b3aaf2cdc79875f83fdd149e1178ce26 ↩︎

3. cnblogs.com/techflow/p/12610616.html
   [^10 ]: https://www.zhihu.com/question/20446337 ↩︎

4. https://zhangzhenhu.github.io/blog/probability_model/5.%E6%97%A0%E5%90%91%E5%9B%BE_lecture_3.html ↩︎

5. 因子图介绍 ↩︎ ↩︎

6. https://zhuanlan.zhihu.com/p/84210564 ↩︎

7. 支持向量机(Support Vector Machine, SVM) ↩︎

8. https://zhuanlan.zhihu.com/p/77750026 ↩︎