MCK矩阵三质量－弹簧系统受激振力

Posted 2022-04-14 studyer_domi

三质量－弹簧系统受激振力，并不考虑各自的阻尼。建立系统运动方程。

 

解：由于阻尼对固有频率没有影响，故本文不研究阻尼的影响， 假定阻尼都为0。原点取在各自静平衡位置。受力分析：

建立运动微分方程：

矩阵形式：

 

假定参数：

m1=1kg、m2=2kg、m3=2kg、k1=5N/m、k2=10N/m 、k3=15N/m、k4=20N/m，

假定p1(t)为单位阶跃响应，p2(t)= p3(t)=0；求解x1(t)变化情况

matlab计算程序：

clc;

close all;

clear;

%% -----------参数----------------

m1=1;%质量参数m1

m2=2;%质量参数m2

m3=2;%质量参数m3

k1=5;%刚度参数k1

k2=10;%刚度参数2

k3=15;%刚度参数k3

k4=20;%刚度参数k4

%% ----------计算-------------

%-------多自由度系统的建模然后找一个方法分析它的振幅 响应，固有频率和主振型

m=[m1 0 0;0 m2 0;0 0 m3]; %质量矩阵

k=[k1+k2 -k2 0;-k2 k2+k3 -k3;0 -k3 k3+k4]; %刚度矩阵

G=inv(m);       %生成质量阵的逆阵

H=G*k;          %生成动力矩阵

[V,D]=eig(H);     %产生特征值与特征向量,D代表特征值,V代表特征向量


f=D/2/pi; %求对应的频率

disp(['固有频率f1=',num2str(f(1,1),'%.4f'),'Hz']) %输出频率

disp(['f1对应主振型',num2str(V(1,1)),' ',num2str(V(2,1)),' ',num2str(V(3,1)),'Hz']) % 输出振型

disp(['固有频率f2=',num2str(f(2,2),'%.4f'),'Hz'])%输出频率

disp(['f2对应主振型',num2str(V(1,2)),' ',num2str(V(2,2)),' ',num2str(V(3,2)),'Hz'])% 输出振型

disp(['固有频率f3=',num2str(f(3,3),'%.4f'),'Hz'])%输出频率

disp(['f3对应主振型',num2str(V(1,3)),' ',num2str(V(2,3)),' ',num2str(V(3,3)),'Hz'])% 输出振型

%-----------振幅,响应------------------

num=[4 0 20 0 -75]; %分子

den=[8 0 100 0 -50 0 375]; %分母

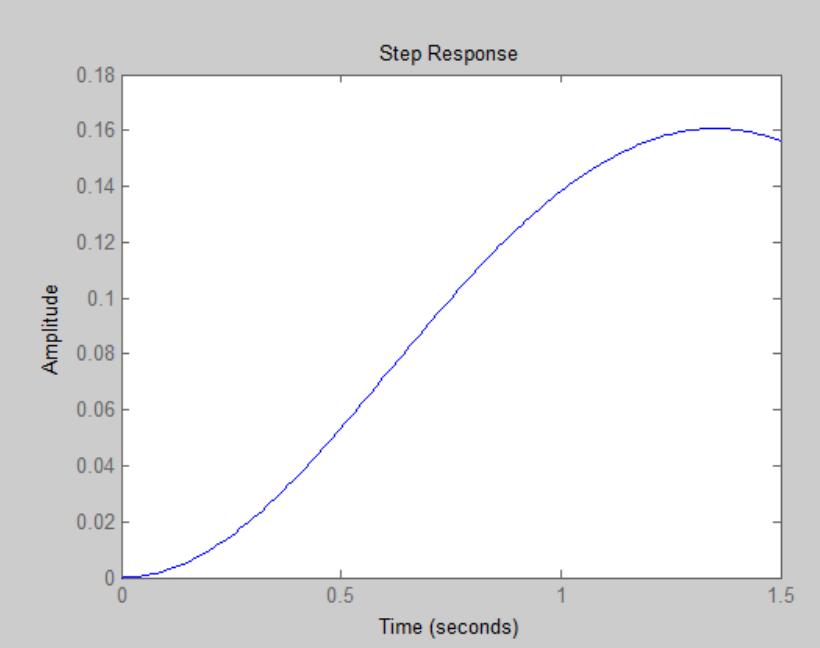
t=0:0.01:1.5; %仿真时间长度

step(num,den,t); %单位阶跃响应

计算结果如下：

固有频率f1=0.6169Hz

f1对应主振型1 1.1124 0.61237Hz

固有频率f2=2.5662Hz

f2对应主振型1 -0.11237 -0.61237Hz

固有频率f3=3.9789Hz

f3对应主振型1 -0.57735 0.57735Hz

x1(t)随时间变化情况