请问在高中数学里求最值是如何运用切比雪夫多项式的。

Posted 2023-05-16

是把二倍角公式cos2Θ=2(cosΘ)^2-1，cos3Θ=4(cosΘ)^3-3cosΘ 的右边cosΘ换成x，得到多项式2x^2-1和4x^3-3x。这两个多项式，又有什么特别的？这些切比雪夫多项式有什么性质？请各位大侠们能否给几个较好的例子？完全不懂额。。。又是如何通过它求出最值的？怎么求的。。。

第一类Chebyshev多项式Tn(x)的最重要的逼近性质是：
在[-1,1]上所有首项系数为1的n次多项式中，Tn(x)/2^n-1对零的偏差最小，也就是说对于任何n次首一多项式p(x)都有max|p(x)| >= max|Tn(x)|/2^n-1。
这个性质的证明要利用Chebyshev交错点定理，应该超出高中知识范围了。这个性质直观的解释是多项式“比较硬”，首项确定之后就不可能通过弯折它让它很好地逼近零了。

作为应用一般来讲是解决min max|p(x)|型的最值问题，其中max的范围是在闭区间[a,b]上，min的范围是对所有满足某一约束的不超过n次的多项式。通常先利用仿射变换把标准区间[-1,1]上的Chebyshev多项式变换到区间[a,b]上再利用最佳逼近性质。 参考技术A 就是换元，相当于把未知数换为我们熟悉的X，但记得，换元时要注意范围的变化。
cosΘ的范围是［—1,1］，所以X的范围也是［—1,1］，如此就可以看成关于X的指数函数了，最值就很好求了。
其实就是把复合函数化为简单函数啦，想想一下，你还是你只是换了一件衣服啊，如果还有什么不懂得就发邮件到[e-mail]吧 参考技术B http://wenku.baidu.com/view/67c159bbfd0a79563c1e7206.html
在谷歌搜索 Chebyshev Polynomial
http://math.fullerton.edu/mathews/n2003/chebyshevpolymod.html 参考技术C 建议你看一下积分形式的切比雪夫不等式

切比雪夫滤波器

切比雪夫滤波器

切比雪夫滤波器，又名“车比雪夫滤波器”，是在通带或阻带上频率响应幅度等波纹波动的滤波器。

1、 切比雪夫滤波器传递函数

$$|H_n(\omega ){|}^2=\frac{1}{1+{ϵ}^2{T_n}^2\frac{\omega }{{\omega }_0}}$$

其中${\omega }_0$为期望截至频率,n为滤波器阶数。

2、切比雪夫多项式

$$V_n(\frac{\omega }{{\omega }_c})=\begin{array}{c}cos(n\ast arccos(\frac{\omega }{{\omega }_c}))|\frac{\omega }{{\omega }_c}|\le 1\\ cosh(n\ast arccosh(\frac{\omega }{{\omega }_c}))|\frac{\omega }{{\omega }_c}|>1\end{array}$$

其中${\omega }_c$为期望截至频率,n为滤波器阶数。

下图为切比雪夫I型滤波器的振幅特性

n为奇数

n为偶数

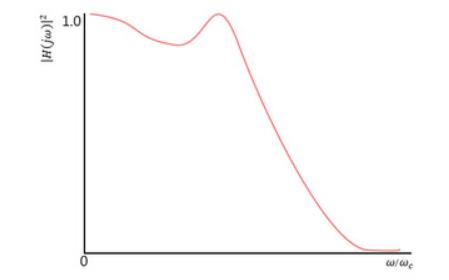
2、特性

1)切比雪夫滤波器是在通带或阻带上频率响应幅度等波纹波动（通带平坦、阻带等波纹或是阻带平坦、通带等波纹）的滤波器，振幅特性在通带内是等波纹。

2)切比雪夫滤波器在过渡带比巴特沃斯滤波器的衰减快，但频率响应的幅频特性不如后者平坦。

3)切比雪夫滤波器和理想滤波器的频率响应曲线之间的误差最小，但是在通频带内存在幅度波动。

4)在通带（或称“通频带”）上频率响应幅度等波纹波动的滤波器称为“I型切比雪夫滤波器”，在阻带（或称“阻频带”）上频率响应幅度等波纹波动的滤波器称为“II型切比雪夫滤波器”

python函数介绍

scipy.signal.iirfilter(N, Wn, rp=None, rs=None, btype='band', analog=False, ftype='butter', output='ba', fs=None)

参数：
N：int  过滤器的顺序。

Wn：array_like  标量或长度为2的序列给出了临界频率(由norm参数定义)。对于模拟滤波器，Wn是角频率(例如rad /s)。

rp：float, 可选参数
对于Chebyshev和椭圆滤波器，可在通带中提供最大纹波。(db)

rs：float, 可选参数
对于切比雪夫和椭圆滤波器，在阻带中提供最小的衰减。(db)

btype：‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’, 可选参数
过滤器的类型。默认值为‘lowpass’。

analog：bool, 可选参数
如果为True，则返回一个模拟滤波器，否则返回一个数字滤波器。

ftype：str, 可选参数
设计的IIR滤波器的类型：Butterworth :‘butter’, Chebyshev I :‘cheby1’, Chebyshev II :‘cheby2’, Cauer/elliptic:‘ellip’, Bessel/Thomson:‘bessel’

output：‘ba’, ‘zpk’, ‘sos’, 可选参数
输出类型：分子/分母(‘ba’)，pole-zero(‘zpk’)或second-order部分(‘sos’)。默认值为‘ba’。

fs：float  可选参数     数字系统的采样频率。
对于数字滤波器，Wn与fs的单位相同。默认情况下，fs为2 half-cycles /sample，因此将它们从0标准化为1，其中1是奈奎斯特频率。 (因此Wn在half-cycles /样本中。)

返回值：
b, a：ndarray，ndarray
IIR滤波器的分子(b)和分母(a)多项式。仅在以下情况下返回output='ba'。

z, p, k：ndarray，ndarray，float
IIR滤波器传递函数的零点，极点和系统增益。仅在以下情况下返回output='zpk'。

sos：ndarray
IIR滤波器的Second-order个部分表示。仅在以下情况下返回output=='sos'。

python例子

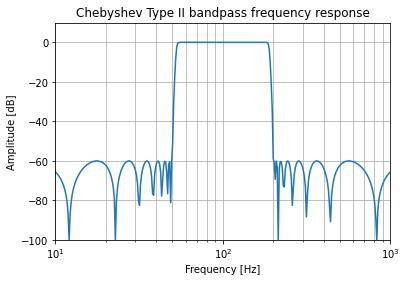
生成一个从50 Hz到200 Hz的17th-order Chebyshev II模拟带通滤波器，并绘制频率响应：

from scipy import signal
import matplotlib.pyplot as plt
import numpy as np

b, a = signal.iirfilter(17, [2*np.pi*50, 2*np.pi*200], rs=60,
                        btype='band', analog=True, ftype='cheby2')    
w, h = signal.freqs(b, a, 1000)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.semilogx(w / (2*np.pi), 20 * np.log10(np.maximum(abs(h), 1e-5)))
ax.set_title('Chebyshev Type II bandpass frequency response')
ax.set_xlabel('Frequency [Hz]')
ax.set_ylabel('Amplitude [dB]')
ax.axis((10, 1000, -100, 10))
ax.grid(which='both', axis='both')
plt.show()

最后附上matlab实现代码，代码来源Blog

%  Cheby1Filter.m
%  切比雪夫Ⅰ型滤波器的设计
%

clear;
close all;
clc;

fs = 1000; %Hz 采样频率
Ts = 1/fs;
N  = 1000; %序列长度
t = (0:N-1)*Ts;
delta_f = 1*fs/N;
f1 = 50;
f2 = 100;
f3 = 200;
f4 = 400;
x1 = 2*0.5*sin(2*pi*f1*t);
x2 = 2*0.5*sin(2*pi*f2*t);
x3 = 2*0.5*sin(2*pi*f3*t);
x4 = 2*0.5*sin(2*pi*f4*t);
x = x1 + x2 + x3 + x4; %待处理信号由四个分量组成

X = fftshift(abs(fft(x)))/N;
X_angle = fftshift(angle(fft(x)));
f = (-N/2:N/2-1)*delta_f;

figure(1);
subplot(3,1,1);
plot(t,x);
title('原信号');
subplot(3,1,2);
plot(f,X);
grid on;
title('原信号频谱幅度特性');
subplot(3,1,3);
plot(f,X_angle);
title('原信号频谱相位特性');
grid on;

%设计一个切比雪夫低通滤波器,要求把50Hz的频率分量保留,其他分量滤掉
wp = 55/(fs/2);  %通带截止频率,取50~100中间的值,并对其归一化
ws = 90/(fs/2);  %阻带截止频率,取50~100中间的值,并对其归一化
alpha_p = 3; %通带允许最大衰减为 db
alpha_s = 40;%阻带允许最小衰减为 db
%获取阶数和截止频率
[N1, wc1] = cheb1ord(wp, ws, alpha_p, alpha_s);
%获得转移函数系数
[b, a] = cheby1(N1,alpha_p,wc1,'low');
%滤波
filter_lp_s = filter(b,a,x);
X_lp_s = fftshift(abs(fft(filter_lp_s)))/N;
X_lp_s_angle = fftshift(angle(fft(filter_lp_s)));
figure(2);
freqz(b,a); %滤波器频谱特性
figure(3);
subplot(3,1,1);
plot(t,filter_lp_s);
grid on;
title('低通滤波后时域图形');
subplot(3,1,2);
plot(f,X_lp_s);
title('低通滤波后频域幅度特性');
subplot(3,1,3);
plot(f,X_lp_s_angle);
title('低通滤波后频域相位特性');



%设计一个高通滤波器,要求把400Hz的频率分量保留,其他分量滤掉
wp = 350/(fs/2);  %通带截止频率,取200~400中间的值,并对其归一化
ws = 380/(fs/2);  %阻带截止频率,取200~400中间的值,并对其归一化
alpha_p = 3; %通带允许最大衰减为  db
alpha_s = 20;%阻带允许最小衰减为  db
%获取阶数和截止频率
[N2, wc2] = cheb1ord( wp , ws , alpha_p , alpha_s);
%获得转移函数系数
[b, a] = cheby1(N2,alpha_p,wc2,'high');
%滤波
filter_hp_s = filter(b,a,x);
X_hp_s = fftshift(abs(fft(filter_hp_s)))/N;
X_hp_s_angle = fftshift(angle(fft(filter_hp_s)));
figure(4);
freqz(b,a); %滤波器频谱特性
figure(5);
subplot(3,1,1);
plot(t,filter_hp_s);
grid on;
title('高通滤波后时域图形');
subplot(3,1,2);
plot(f,X_hp_s);
title('高通滤波后频域幅度特性');
subplot(3,1,3);
plot(f,X_hp_s_angle);
title('高通滤波后频域相位特性');


%设计一个带通滤波器,要求把50Hz和400Hz的频率分量滤掉,其他分量保留
wp = [65 385] / (fs/2);  %通带截止频率,50~100、200~400中间各取一个值,并对其归一化
ws = [75 375] / (fs/2);  %阻带截止频率,50~100、200~400中间各取一个值,并对其归一化
alpha_p = 3; %通带允许最大衰减为  db
alpha_s = 20;%阻带允许最小衰减为  db
%获取阶数和截止频率
[N3, wn] = cheb1ord( wp , ws , alpha_p , alpha_s);
%获得转移函数系数
[b, a] = cheby1(N3,alpha_p,wn,'bandpass');
%滤波
filter_bp_s = filter(b,a,x);
X_bp_s = fftshift(abs(fft(filter_bp_s)))/N;
X_bp_s_angle = fftshift(angle(fft(filter_bp_s)));
figure(6);
freqz(b,a); %滤波器频谱特性
figure(7);
subplot(3,1,1);
plot(t,filter_bp_s);
grid on;
title('带通滤波后时域图形');
subplot(3,1,2);
plot(f,X_bp_s);
title('带通滤波后频域幅度特性');
subplot(3,1,3);
plot(f,X_bp_s_angle);
title('带通滤波后频域相位特性');


%设计一个带阻滤波器,要求把50Hz和400Hz的频率分量保留,其他分量滤掉
wp = [65 385 ] / (fs/2);  %通带截止频率?,50~100、200~400中间各取一个值,并对其归一化
ws = [75 375 ] / (fs/2);  %阻带截止频率?,50~100、200~400中间各取一个值,并对其归一化
alpha_p = 3; %通带允许最大衰减为  db
alpha_s = 20;%阻带允许最小衰减为  db
%获取阶数和截止频率
[N4, wn] = cheb1ord( wp , ws , alpha_p , alpha_s);
%获得转移函数系数
[b, a] = cheby1(N4,alpha_p,wn,'stop');
%滤波
filter_bs_s = filter(b,a,x);
X_bs_s = fftshift(abs(fft(filter_bs_s)))/N;
X_bs_s_angle = fftshift(angle(fft(filter_bs_s)));
figure(8);
freqz(b,a); %滤波器频谱特性
figure(9);
subplot(3,1,1);
plot(t,filter_bs_s);
grid on;
title('带阻滤波后时域图形');
subplot(3,1,2);
plot(f,X_bs_s);
title('带阻滤波后频域幅度特性');
subplot(3,1,3);
plot(f,X_bs_s_angle);