普朗克公式推导
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了普朗克公式推导相关的知识,希望对你有一定的参考价值。
求助啊
要求从能量量子化角度出发,推导出planck公式,要求给出完整的推导过程和参考文献的名称
希望尽快能给以答复
谢谢
可以直接在网上找到推导过程也可以
黑体辐射的能量是由电磁场的本征振动引起的,为简化推导过程,在此将黑体简化为边长为L的正方形谐振腔。如图示:
则腔内的电磁场满足亥姆霍兹方程:
(1)
用分离变量法,令
则(1)式可分解为三个方程:
其中
得(1)式的驻波解为:
由在x=0,x=L,y=0,y=L,z=0,z=L上的边界条件 及 可得:
, ,
(其中 , , 满足关系 )
则 (j表示第j个本征态)的绝对值为:
换成第j个本征态的频率得:
当 时, 和 可视为连续变化,不必取分立值,即有:
(2)
(2)式表明在整数n空间一组整数 即对应一个本征模的频率。因此,频率区间 内的本征模数,在数值上等于整数n空间内数值半径由 范围内球壳体积的八分之一,即:
(V为腔的体积)
又因为每一个频率为 的单色平面波还存在着两个独立的相互垂直的偏振态,则频率间隔 内的本征模数为:
设 表示温度为T,频率为 的本征振动的平均能量, 为相应的能量密度,则振动频率在 到 之间的能量为:
(3)
本征振动是简谐振动,由三维谐振子的能量本征值: (n=0,1,2…)
系统处于热平衡状态时,处于各本征能量的谐振子分布遵从麦克斯韦-波尔兹曼分布律:
即:
所以: (4)
若令 ,
则(4)式可改写为:
由
所以:
代入(3)式得:
此即为Planck黑体辐射公式。
若按经典理论,由热力学与统计物理的能量均分定理可知平均能量为:
则:
此即为Rayleigh-Jeans黑体辐射公式。
两公式的曲线与实验曲线的符合情况如图:
参考资料:http://202.113.227.137/songz/shen/qm_ehomework/2006/lz/work/0310340.doc
参考技术A 利用光电效应现象测定普朗克常数一、实验原理
光电效应的实验原理如(图1)所示。入射光照射到光电管阴极上,产生的光电子在电场的作用下向阳极迁移构成光电流,改变外加电压,测量出光电流的大小,既可得出光电管的伏安特性曲线。
爱因斯坦提出著名的光电效应方程:
(为金属的溢出功,为电子获得的初始动能) (1)
阳极电位为于截止电压,光电流才为零,此时有关系式:(2)
将(2)式代入(1)式可得: 或 (3)
上式表明截止电压是频率的线性函数,直线的斜率为,只要用实验的方法得出不同的频率对应的截止电压,求出直线的斜率,就可算出普朗克常数。
二、实验仪器:ZKY-GD-4智能光电效应(普朗克常数)实验仪
三、实验要求:
用两种方法求出普朗克常数:
1.作图法求普朗克常数
通过实验数据,得出-直线的斜率,即可用求出普朗克常数,并与的公认值比较求出相对误差,式中,。
2.用最小二乘法处理数据求出普朗克常数
四、数据记录及处理:(举例)
波 长(nm)
365.0
404.7
435.8
546.1
577.0
频率
8.214
7.408
6.879
5.530
5.196
截止电压
手动
1.792
1.488
1.242
0.688
0.542
自动
1.792
1.490
1.244
0.688
0.546
平 均 值
1.792
1.489
1.243
0.688
0.544
1. 用做图法求普朗克常数:(坐标纸上作图)
由图得直线上两点的坐标为 、
于是得直线的斜率为:
普朗克常数为:
相对误差为:
2. 最小二乘法求普朗克常数:
用表示频率,用表示截止电压,根据最小二乘法得:
直线的斜率为:
比较两种方法可看出:
1. 通过作图法求普朗克常数比较直观,但由于数据点太少,所做直线斜率变化比较大,于是误差也比较大。(见图)
2. 应用最小二乘法求普朗克常数,计算过程比较繁琐,但从公式的推倒过程可以看出结果较为可靠。
五、实验注意事项:
1. 要正确连线并调试仪器。
2. 实验结束后及时按要求关闭仪器,注意保护光电管。
六、思考题
1. 光电效应的实验规律有哪几方面?用波动理论去解释时遇到了那些困难?
2. 根据爱因斯坦的光子假说,如何解释光电效应的实验结果 参考技术B 对不起不会呀!
MFC输出普朗克常数
在量子力学中可以计算德布罗意波长,其公式如下;
德布罗意波长 = h / (质量 * 速度);

其中h是普朗克常数;
先看一下普朗克常数;6.62 乘以10的负34次方;
输出一下此常数看一下;
#define PLK 6.62 * (10E-34)
void CDblyView::OnDraw(CDC* pDC)
CDblyDoc* pDoc = GetDocument();
ASSERT_VALID(pDoc);
// TODO: add draw code for native data here
CString str1, str2;
str1.Format("%E",PLK);
pDC->TextOut(20,20,str1);
str2.Format("%.20lf", PLK);
pDC->TextOut(20,50,str2);
str2.Format("%.40lf", PLK);
pDC->TextOut(20,80,str2);
str2.Format("%lf", PLK);
pDC->TextOut(20,110,str2);
先#define定义常量;小数点位数太多一般用E的形式定义常数;
#define PLK 6.62 * (10E-34)
#define PLK 6.62 * 10E-34
E的后面是指数部分;
两种写法一样,10E-34,自己会识别E的后面的指数部分;
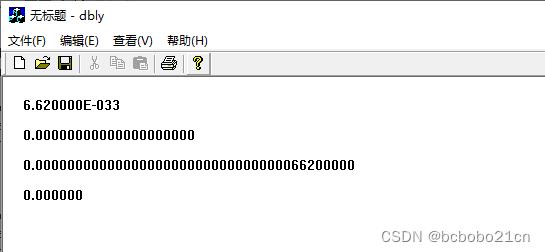
以E的表示法输出使用%E;
输出小数是使用"%lf",默认输出6位小数;
如果只输出6位,看不到完整数值;
输出20位小数,"%.20lf",也看不到完整数值;
输出40位小数,"%.40lf",可以看到完整数值;
以上是关于普朗克公式推导的主要内容,如果未能解决你的问题,请参考以下文章