聚类分析二：DBSCAN算法

Posted 2020-11-19 xyp666

一.基本概念

dbscan算法

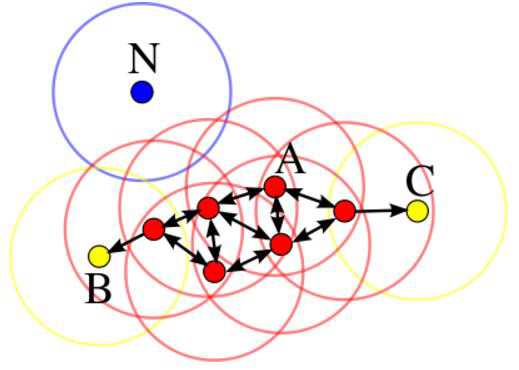
• 核心对象(A)：若某个点的密度达到算法设定的阈值则其为核心点（即r邻域内点的数量不小于minPts）
• 邻域的距离阈值：设定的半径r
• 直接密度可达：若某点p在点q的r邻域内且q是核心点，则p-q是直接密度可达（核心对象，在邻域内）
• 密度可达：若有一个点的序列q0、q1....qk，对任意qi-qi-1是直接密度可达，则称从q0到qk密度可达，这实际是直接密度可达的传播（直接密度可达传播）
• 密度相连：若从某核心点p出发，点q和点k都是密度可达的，则称点q和点k是密度相连
• 边界点(B、C)：属于某一个类的非核心点，不能发展下线了
• 噪声点(N)：不属于任何一个类簇的点，从任何一个核心点出发都是密度不可达的

 

二.基本过程

算法流程：（数据集、半径、密度阈值）

• 标记所有对象都为没有访问过
• 随机选择一个没有访问过的对象p，标记p为已访问过
• 如果p的邻域至少有minpts个对象

1. 创建一个新簇c，并把p添加到c中
2. 令N为p的领域中的对象集合
3. 对于N中每一个点：如果p是没有访问过，标记p为已访问过。且如果p的邻域至少有minpts个对象，把这些对象添加到N；如果p还不是任何簇的成员，把p添加到c

• 否则标记p为噪音
• 直到没有标记为没有访问过的对象

参数选择：

• 半径：可以根据k距离来设定：找突变点K距离

  K距离：给定数据集P={p(i); i=0,1,…n}，计算点P(i)到集合D的子集S中所有点
  之间的距离，距离按照从小到大的顺序排序，d(k)就被称为k-距离。

• minpts：k-距离中k的值，一般取的小一些，多次尝试

 

 

三.优缺点

优势

• 不需要指定簇的个数
• 可以发现任意形状的簇
• 擅长找到离群点
• 只需两个参数

劣势

• 高维数据有些困难（可以做降维）
• 参数难以选择，但对结果的影响非常大
• sklearn中效率很慢（数据削减策略）