SPSS分析中解释的总方差和旋转成分矩阵要怎么进行解释？就是说怎么对这个结果进行说明，然后写进论文里？

Posted 2023-04-17

最大方差旋转只是其中的一种旋转方法，因为该方法旋转后的结果很清楚，所以一般默认选择都是这种方法 至于做主成分分析，是需要看原始数据情况的，如果原始数据变量就很少，不超过三五个这样的，就没必要做主成分分析。

扩展资料：

SPSS之方差分析总结

1，从自变量和因变量的数目上看，如果只有一个自变量和一个因变量，那我们采用“单因素方差分析”；如果有多个自变量和一个因变量，那我们采用“多因素方差分析”；如果有一个自变量和多个因变量，采用“单因素多元方差分析”；如果有多个自变量和多个因变量，则采用“多因素多元方差分析”。

2，其中，“单因素多元方差分析”和“多因素多元方差分析”统称为“多元方差分析，在SPSS上的实现步骤完全一致。

3，另外，对于“协方差分析”法，大家可以将其理解为“控制变量法”，即控制一个因素不变，研究其他因素对试验结果的影响。其中，需要控制的变量就是“协方差分析”中的协变量。而“重复测量方差分析”和字面意义一样，当我们需要对观测结果进行多次取值时，该方法即是最好的选择。

4，从数据结构方面来看，细心的朋友可能已经从前面的几章中发现，方差分析的数据都要求“数值型”，变量类型可以为“分类变量”，也可为数值变量。之所以补充此处，是因为在SPSS软件中，如果不事先设置好相关数据结构，可能在SPSS操作时你会发现有些按钮是灰色的，点不了。

参考技术A

最大方差旋转只是其中的一种旋转方法，因为该方法旋转后的结果很清楚，所以一般默认选择都是这种方法，至于做主成分分析，是需要看原始数据情况的，如果原始数据变量就很少，不超过三五个这样的，就没必要做主成分分析。

看数据应该是做主成分分析的变量也就只有2个，这样根本没必要做主成分分析。

因子分析模型中，假定每个原始变量由两部分组成：共同因子和唯一因子。共同因子是各个原始变量所共有的因子，解释变量之间的相关关系。

扩展资料：

唯一因子顾名思义是每个原始变量所特有的因子，表示该变量不能被共同因子解释的部分。

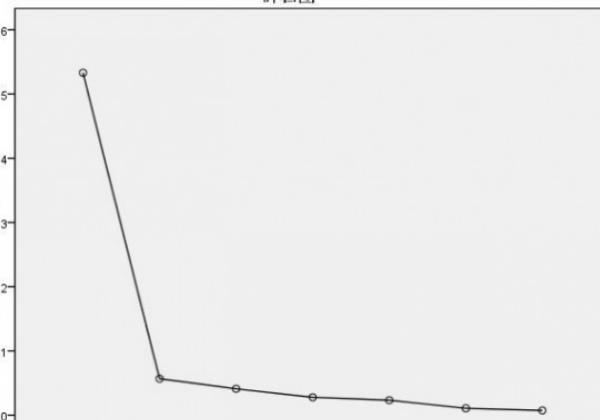
主成分分析是试图寻找原有变量的一个线性组合。这个线性组合方差越大，那么该组合所携带的信息就越多。也就是说，主成分分析就是将原始数据的主要成分放大。

因子分析，它是假设原有变量的背后存在着一个个隐藏的因子，这个因子可以可以包括原有变量中的一个或者几个，因子分析并不是原有变量的线性组合。

一般来说方法都选择主成分方法，但是在python中进行因子分析时用的不是这个方法。

参考资料来源：百度百科——spss

参考技术B 最大方差旋转 只是其中的一种旋转方法，因为该方法旋转后的结果很清楚，所以一般默认选择都是这种方法 至于你做主成分分析 是需要看你的原始数据情况的，如果你原始数据变量就很少，不超过三五个这样的，就没必要做主成分分析。看 看你的数据应该是做主成分分析的变量也就只有2个吧 这样根本没必要做主成分分析本回答被提问者和网友采纳

如何用SPSS进行多因素方差分析

参考技术A 2.假设方差不齐时又有一系列的分析方法可选。 再者，为保证统计准确，如果方差不齐，可以进行对数，倒数或函数的转换，选择适当的转换形式，直到齐性检验变为不显著。 如果还不行就只能用非参数的单因素分析。如果非要进行方差分析则需要把means±SD范围外的数据剔除。 实际操作中对方差齐性等适用条件的把握: 1.单因素方差分析:根据BOX的研究结果,在单因素方差分析中,如果各组的例数相同(即均衡),或总体呈正态分布,则方差分析模型对方差略微不齐有一定的耐受力,只要最大与最小方差之比小于3,分析结果都是稳定的 2. 单元格内无重复数据的方差分析分析:以配伍设计的方差分析最为典型,此时不需要考虑正态性和方差齐性问题,原因在于正态性和方差齐性的考察是以单元格为基本单位的,此时每个格子中只有一个元素,当然没法分析了.除配伍设计的方差分析外,交叉设计,正交设计等也可以出现无重复数据的情况.但必须指出,这里只是因条件不足,无法考察适用条件,而不是说可以完全忽视这两个问题.如果根据专业知识认为可能在不同单元格内正态性,方差齐性有问题,则应当避免使用这种无重复数据的设计方案. 3.有重复数据的多因素方差分析：由于正态性,方差齐性的考察以单元格为基本单位，此时单元格数目往往很多，平均每个单元格内的样本粒数实际上比较少。此时实际上很难检验出差别；另一方面，也可能只是因为极个别单元格方差不齐而单质检验不能通过。