密码学中的承诺
Posted Amire0x
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了密码学中的承诺相关的知识,希望对你有一定的参考价值。
Commitment
概述
密码学承诺是一个涉及两方的二阶段交互协议,双方分别为承诺方和接收方。简述来说,它的功能涵盖不可更改性和确定性。
承诺方发送的消息密文,一旦发出就意味着不会再更改,而接收方收到这个消息可以进行验证结果。
特点就是无需第三方就可以进行验证。
举个例子:猜拳问题
假设有人在猜拳中老是不按时出拳,那么在看到对方的结果再出拳,显然是不公平的,在没有第三方的情况下,怎样保证无人作弊呢?那就是承诺。
这里使用一个哈希函数构造一个简单的承诺方案,双方选取一个足够安全的哈希函数
H
(
x
)
H(x)
H(x),将猜拳的三种出拳方法定为一组数字如
x
1
,
x
2
,
x
3
x_1,x_2,x_3
x1,x2,x3。那么方案如下,
- 选手一选择一个出拳方法 x i x_i xi(如 x 1 x_1 x1),再选取一个随机数 r i r_i ri如( r 1 r_1 r1),计算承诺 H ( x 1 ∣ ∣ r 1 ) H(x_1||r_1) H(x1∣∣r1),并把它发送给选手二。
- 选手二也选择一个出拳方法(如 x 3 x_3 x3),同样也选择一个随机数 r 2 r_2 r2,计算承诺 H ( x 2 ∣ ∣ r 2 ) H(x_2||r_2) H(x2∣∣r2),并把它发送给选手一。
- 双方都收到承诺后,都公布自己的 x i x_i xi和 r i r_i ri,然后进行验证即可
选择添加随机数的原因主要预防某一方直接算出三种出拳方式的哈希,然后接收到了另一方的哈希后,直接进行对比作弊。
可以看到承诺主要分为两个阶段
- Commit Phase:把暂时不想公开的消息(即前面的出拳方案)再加一个随机数,加密后(如前面的计算哈希)发送给对方;
- Reveal Phase:公开秘密和随机数。
性质
承诺具有两个基本性质:隐藏性(Hiding)和绑定性(Binding),隐藏也就是承诺值是不会泄漏有关原消息的任何信息的,而绑定就是接收方可以确信收到的消息是该承诺对应的消息,不可能再找到一个不同的消息从而诞生同一个承诺。
而衡量性质强度一般有两个标准 Perfectly和Computationally,前者代表即便有无穷计算能力也不能破坏掉该性质,后者则是以目前的计算能力在可忍受的时间里是不能破坏该性质的。
但不存在Perfectly Hiding和Perfectly Binding,假设存在一个Perfectly Hiding,那么为了不泄露原消息,一定会有多个消息能计算出同一个承诺,这恰好违背了Binding的性质。
常用方案
主要是拥有Perfectly hiding and computationally binding的Pedersen Commitment 和 拥有Perfectly binding but computationally hiding的 ElGamal Commitment
Pedersen Commitment
DL(离散对数)
选择一个阶为 q q q的乘法群 G G G,再选择两个元素 g , h ∈ G q g,h \\in G_q g,h∈Gq, x x x是消息, r r r是随机数
- Commit Phase: C o m m i t ( x , r ) = g x h r Commit(x,r)=g^xh^r Commit(x,r)=gxhr
- Reveal Phase:公开 x , r x,r x,r
加同态
C
o
m
m
i
t
(
x
1
,
r
1
)
×
C
o
m
m
i
t
(
x
2
,
r
2
)
=
g
x
1
h
r
1
×
g
x
2
h
r
2
=
g
x
1
+
x
2
h
r
1
+
r
2
=
C
o
m
m
i
t
(
x
1
+
x
2
,
r
1
+
r
2
)
\\beginaligned Commit(x_1,r_1) \\times Commit(x_2,r_2) &= g^x_1h^r_1 \\times g^x_2h^r_2\\\\ &=g^x_1+x_2h^r_1+r_2 \\\\ &=Commit(x_1+x_2,r_1+r_2) \\endaligned
Commit(x1,r1)×Commit(x2,r2)=gx1hr1×gx2hr2=gx1+x2hr1+r2=Commit(x1+x2,r1+r2)
ECC(椭圆曲线)
选择椭圆曲线上的一个基点 G G G和随机一个点 H H H
- Commit Phase: C o m m i t ( x , r ) = G x + H r Commit(x,r)=Gx+Hr Commit(x,r)=Gx+Hr
- Reveal Phase:公开 x , r x,r x,r
加同态
$\\beginaligned
\\endaligned$
C
o
m
m
i
t
(
x
1
,
r
1
)
+
C
o
m
m
i
t
(
x
2
,
r
2
)
=
G
x
1
+
H
r
1
+
G
x
2
+
H
r
2
=
(
x
1
+
x
2
)
G
+
(
r
1
+
r
2
)
H
=
C
o
m
m
i
t
(
x
1
+
x
2
,
r
1
+
r
2
)
\\beginaligned Commit(x_1,r_1) + Commit(x_2,r_2) &= Gx_1+Hr_1 + Gx_2+Hr_2 \\\\ &=(x_1+x_2)G+(r_1+r_2)H \\\\ &=Commit(x_1+x_2,r_1+r_2) \\endaligned
Commit(x1,r1)+Commit(x2,r2)=Gx1+Hr1+Gx2+Hr2=(x1+x2)G+(r1+r2)H=Commit(x1+x2,r1+r
Pederson承诺是密码学中承诺的一种,1992年被Torben Pryds Pedersen在“Non-Interactive and Information-Theoretic Secure Verifiable Secret Sharing”一文中提出。 以结合椭圆曲线为例来说明,Pedersen承诺核心公式表达: C = r * G + v * H 上述公式中,C为生成的承诺值,G、H为特定椭圆曲线上的生成点,r代表着盲因子(Blinding factor),v则代表着原始信息。由于G、H为特定椭圆曲线上的生成点,所以r * G、v * H可以看作是相应曲线上的公钥(r、v同理也可以视为私钥)。 承诺生成和揭露过程如图: 由于引入了随机盲因子r,对于同一个v会就能产生不同的承诺c,即便敏感隐私数据v不变,最终的承诺c也会随着r的变化而变化,因此提供了信息论安全的隐匿性。这一点类似ECDSA,Schnorr签名采用的手法。 Pedersen承诺还具有加法同态特性。所谓加法同态,即两数相加和的密文等于两数的密文相加!假设明文a, b ,加密函数e,满足: Pedersen承诺结合椭圆曲线天然地具备了加法同态的特性,这是椭圆曲线点运算的性质决定的。 假设有两个要承诺的信息v1,v2, 随机数r1,r2,生成对应的两个承诺: 则v1+v2承诺结果: Pedersen承诺还可以扩展构造v1∗v2等复杂的情况,来证明新产生的承诺满足与原始承诺之间存在指定的约束关系。 Pedersen承诺产生方式,有些类似加密,签名之类的算法。但是,作为密码学承诺重在“承诺”,并不提供解密算法,即如果只有r,无法有效地计算出隐私数据v。 目前Pedersen承诺在区块链中的应用主要在隐私币中,如zcash,MimbleWimble,Monero等。介绍
目前Pedersen Commitment主要搭配椭圆曲线密码学使用(当然也可以结合指数运算)。具有基于离散对数困难问题的强绑定性和同态加法特性的密文形式。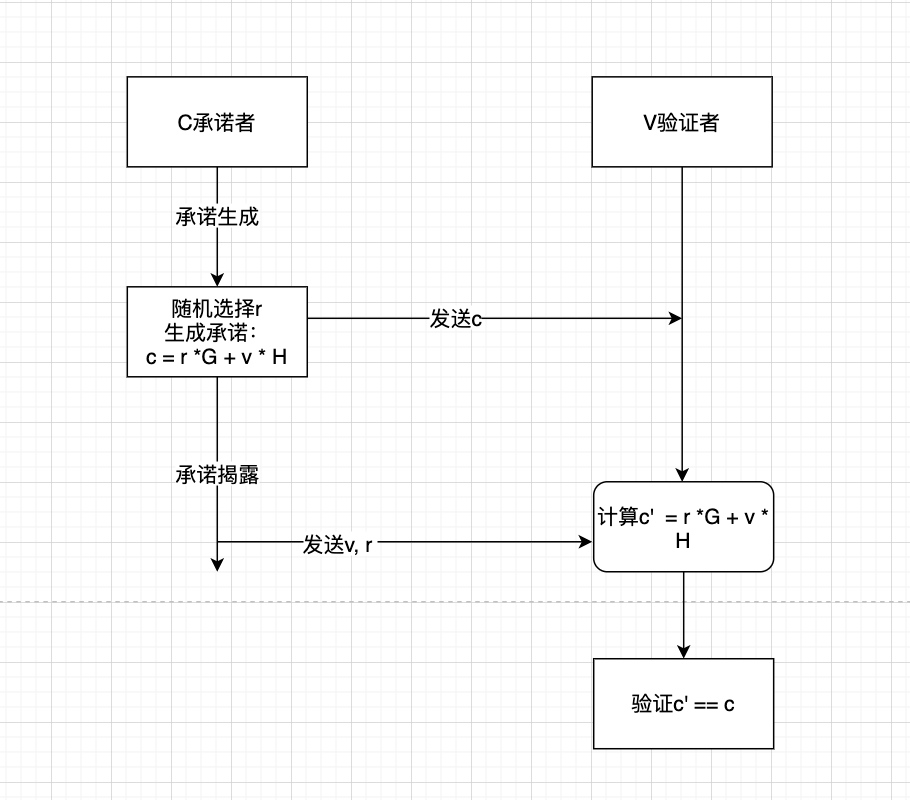
Pedersen承诺加法同态
c = a + b
e(a) + e (b) = e(c)
C(v1)=r1∗G+v1∗H
C(v2)=r2∗G+v2∗H
C(v1+v2)=(r1+r2)G+(v1+v2)∗H
(r1G+v1∗H)+(r2∗G+v2∗H)
C(v1)+C(v2)小结