密码学基础：Pedersen Commitment

Posted 2021-09-03 CNFINIT

介绍

       Pederson承诺是密码学中承诺的一种，1992年被Torben Pryds Pedersen在“Non-Interactive and Information-Theoretic Secure Verifiable Secret Sharing”一文中提出。
目前Pedersen Commitment主要搭配椭圆曲线密码学使用（当然也可以结合指数运算）。具有基于离散对数困难问题的强绑定性和同态加法特性的密文形式。

        以结合椭圆曲线为例来说明，Pedersen承诺核心公式表达：

        C = r * G + v * H

       上述公式中，C为生成的承诺值，G、H为特定椭圆曲线上的生成点，r代表着盲因子（Blinding factor），v则代表着原始信息。由于G、H为特定椭圆曲线上的生成点，所以r * G、v * H可以看作是相应曲线上的公钥（r、v同理也可以视为私钥）。

承诺生成和揭露过程如图：

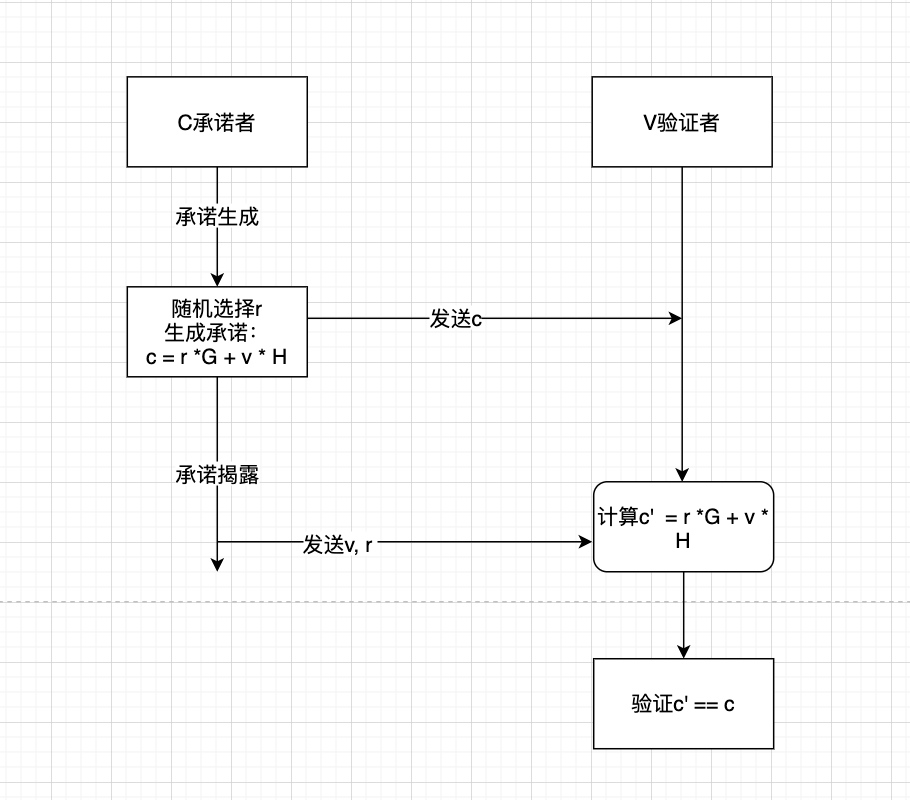
       由于引入了随机盲因子r，对于同一个v会就能产生不同的承诺c，即便敏感隐私数据v不变，最终的承诺c也会随着r的变化而变化，因此提供了信息论安全的隐匿性。这一点类似ECDSA，Schnorr签名采用的手法。

Pedersen承诺加法同态

       Pedersen承诺还具有加法同态特性。所谓加法同态，即两数相加和的密文等于两数的密文相加！假设明文a, b ,加密函数e，满足：
       c = a + b
       e(a) + e (b) = e(c)

       Pedersen承诺结合椭圆曲线天然地具备了加法同态的特性，这是椭圆曲线点运算的性质决定的。

       假设有两个要承诺的信息v1​,v2​, 随机数r1​,r2​,生成对应的两个承诺：
       C(v1​)=r1​∗G+v1​∗H
       C(v2​)=r2​∗G+v2​∗H

       则v1​+v2​承诺结果：
       C(v1​+v2​)=(r1​+r2​)G+(v1​+v2​)∗H
       (r1​G+v1​∗H)+(r2​∗G+v2​∗H)
       C(v1​)+C(v2​)

       Pedersen承诺还可以扩展构造v1​∗v2​等复杂的情况，来证明新产生的承诺满足与原始承诺之间存在指定的约束关系。

小结

        Pedersen承诺产生方式，有些类似加密，签名之类的算法。但是，作为密码学承诺重在“承诺”，并不提供解密算法，即如果只有r，无法有效地计算出隐私数据v。

       目前Pedersen承诺在区块链中的应用主要在隐私币中，如zcash,MimbleWimble,Monero等。