sCrypt 合约中的椭圆曲线算法：第二部分

Posted 2022-12-14 sCrypt 智能合约

我们在脚本中实现了椭圆曲线 (EC) 算法。在之前的实现中，我们进行链下计算并在脚本中验证结果。我们这里直接用脚本计算。

基于EC的应用非常多，特别是在密码学领域，如数字签名、加密、承诺方案等。作为具体示例，我们重新实现了 ECDSA 签名验证，允许使用任意消息验证签名。

模逆

在实现点加法和乘法之前，我们先介绍模逆，因为它是一个积木。

整数 a 的模乘逆是整数 x，使得 a*x ≡ 1 mod n。为了导出该值，我们使用扩展欧几里得算法 (eGCD)。因为在使用 EC 算法时模逆会占用大部分脚本大小，所以尽可能优化它是至关重要的。因此，我们使用内联汇编直接在原始脚本中对其进行编码。

扩展欧几里德算法

扩展欧几里德算法是对标准欧几里德算法的扩展。除了找到最大公约数 (GCD) 之外，它还计算 Bézout 恒等式的系数，它们是整数 x 和 y，使得：

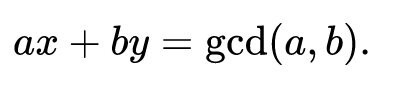
eGCD算法定义如下：

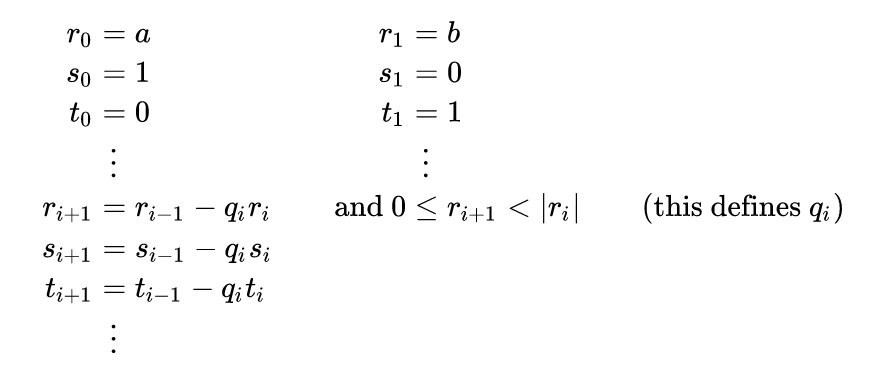
当余数 r(i+1) 为 0 时停止执行。如果 a 和 b 是互质的（在 EC 算法中它们总是应该互质，因为曲线参数 p 和 n 是质数），x 也是 a mod b 的模逆。

下面是输入a=240，b=46的eGCD算法的示例计算表：

资料来源： 维基百科

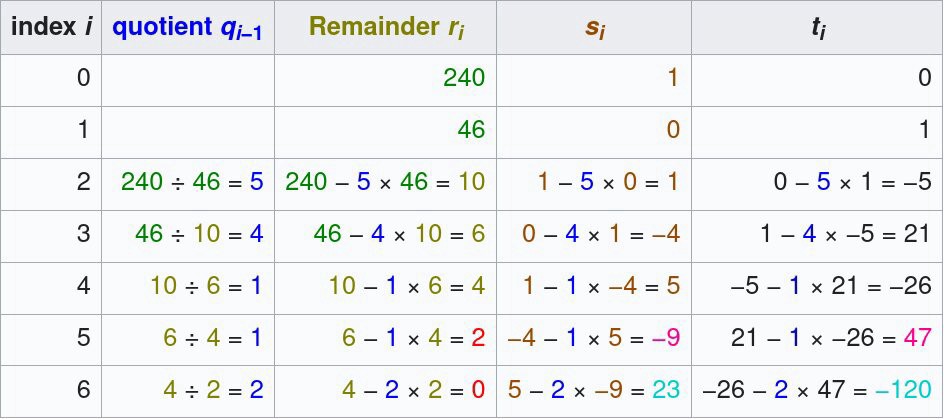
实现

以下是扩展欧几里德算法在 Script 中的高度优化实现。因为我们只对 t(i) 序列感兴趣，所以我们不需要跟踪 s(i) 序列，从而使脚本大小更小。

static function modInverseEGCD(int x, int n) : int 
    // The following script already does modular reduction at the start so there's no
    // need to normalize x before function call.
    asm 
        OP_2DUP OP_MOD OP_DUP OP_0 OP_LESSTHAN OP_IF OP_DUP OP_2 OP_PICK OP_ADD OP_ELSE OP_DUP OP_ENDIF OP_NIP OP_2 OP_ROLL OP_DROP
        OP_DUP OP_TOALTSTACK OP_TOALTSTACK OP_TOALTSTACK
        OP_1 OP_0 OP_1
        loop(UB) 
            OP_FROMALTSTACK OP_FROMALTSTACK OP_2DUP OP_DUP OP_IF OP_TUCK OP_MOD OP_TOALTSTACK OP_TOALTSTACK OP_DIV OP_MUL OP_SUB OP_TUCK OP_ELSE OP_TOALTSTACK OP_TOALTSTACK OP_DROP OP_DROP OP_ENDIF
        
        OP_FROMALTSTACK OP_FROMALTSTACK OP_DROP OP_DROP OP_DROP OP_FROMALTSTACK OP_SWAP OP_NIP
    

源代码

计算循环的上限

k 位模数 n 的迭代次数上限可以使用以下等式导出：

，其中 phi 是黄金比例：

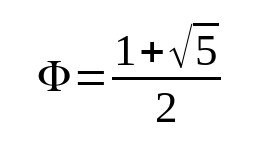
对于 256 位的模数，如比特币曲线 secp256k1，我们得到 368 的上限。modInverseEGCD() 生成的脚本大小约为 7 KB。

点加法

椭圆曲线上的加点定义为​​通过点 P 和 Q 的直线的曲线交点的负值。如果其中一个点是无限点 (0, 0)，我们只返回另一个点。

static function addPoints(Point p, Point q) : Point 
    Point ret = 0, 0;

    if (p.x == 0 && p.y == 0) 
        // if P == inf -> P + Q = Q
        ret = q;
     else if (q.x == 0 && q.y == 0) 
        // if Q == inf -> P + Q = P
        ret = p;
     else 
        int lambda = 0;
        if (p.x == q.x && p.y == q.y) 
            lambda = (3 * p.x * p.x) * modInverseEGCD(2 * p.y, P);
         else 
            lambda = (q.y - p.y) * modInverseEGCD(q.x - p.x, P);
        

        int rx = modReduce(lambda * lambda - p.x - q.x, P);
        int ry = modReduce(lambda * (p.x - rx) - p.y, P);

        ret = rx, ry;
    

    return ret;

源代码

点加倍

如果 P 和 Q 处于同一坐标，我们使用曲线在该坐标处的切线交点。

static function doublePoint(Point p) : Point 
    int lambda = (3 * p.x * p.x) * modInverseEGCD(2 * p.y, P);

    int rx = modReduce(lambda * lambda - 2 * p.x, P);
    int ry = modReduce(lambda * (p.x - rx) - p.y, P);
    
    Point res = rx, ry;
    return res;

源代码

标量乘法

点与标量的乘法是我们定义的计算量最大的函数。为简单起见，我们使用了双倍-加法算法。还有其它更高效的方法。

static function multByScalar(Point p, int m) : Point 
    // Double and add method.
    // Lowest bit to highest.
    Point n = p;
    Point q = 0, 0;

    bytes mb =   reverseBytes(num2bin(m, S), S);
    bytes mask = reverseBytes(num2bin(1, S), S);
    bytes zero = reverseBytes(num2bin(0, S), S);

    loop (256) : i 
        if ((mb & (mask << i)) != zero) 
            q = addPoints(q, n);
        

        n = doublePoint(n);
    

    return q;

源代码

ECDSA 签名验证

现在我们已经实现了所有需要的 EC 原语，我们可以定义一个函数来检查任意消息签名的有效性，而无需任何新的操作码，例如 BTC 上的 OP_CHECKSIGFROMSTACK 或 BCH 上的 OP_DATASIGVERIFY（又名 OP_CHECKDATASIG）。

static function verifySig(bytes m, Signature sig, Point pubKey) : bool 
    Sha256 hash = hash256(m);
    int hashInt = unpack(reverseBytes(hash, 32));

    require(sig.r >= 1 && sig.r < n && sig.s >= 1 && sig.s < n);

    int sInv = modInverseEGCD(sig.s, n);
    int u1 = modReduce(hashInt * sInv, n);
    int u2 = modReduce(sig.r * sInv, n);

    Point U1 = multByScalar(G, u1);
    Point U2 = multByScalar(pubKey, u2);
    Point X = addPoints(U1, U2);

    return sig.r == X.x;

正如我们所见，该函数调用了两次标量乘法。单次调用 multByScalar() 会花费我们大约 5 MB 的脚本大小。因此，单个签名验证大约需要 10 MB 的脚本，可以进一步优化。我们甚至可以使用自定义曲线而不是标准的 secp256k1 并使用更大的密钥大小来显着提高安全性。

致谢

这是 nChain 白皮书 1611 的实现。